数据结构(18)--Prim算法求解无向网的最小生成树

参考书籍：数据结构（C语言版）严蔚敏吴伟民编著清华大学出版社

1.最小生成树

    对于带权的连通图(连通网)G，其生成树也是带权的，将权值之和最小的生成树称为最小生成树。

    最小生成树的MST性质：
    假设 N =（V,{E}）是一个连通网，U是顶点集 V 的一个非空子集。若（u,v）是一条具有最小权值（代价）的边，其中 u ∈U，v∈V-U，则必存在一棵包含边（u,v）的最小生成树。

2.普里姆（Prim）算法

    基本思想：
    (1)假设 G=(V,{E}) 是一个具有 n 个顶点的连通网络，T=(U，{TE})是 G 的最小生成树，其中 U 是 T 的顶点集，TE 是 T 的边集，U 和 TE 的初值均为空；
    (2)从 V 中任取一个顶点（假定为 V1），将此顶点并入 U中，此时最小生成树顶点集 U={V1}；
    (3)从那些其中一个端点已在 U 中，另一端点仍在 U 外的所有边中，找一条最短（即权值最小）的边，设该边为(Vi,Vj)，其中 Vi∈U，Vj∈V-U，并把该边和顶点 Vj分别并入 T 的边集 TE 和顶点集 U；
    (4)如此进行下去，每次往生成树里并入一个顶点和一条边，直到 n-1 次后，把所有 n 个顶点都并入生成树 T 的顶点集 U 中，此时 U=V，TE中包含有（n-1）条边；这样，T 就是最后得到的最小生成树。

    算法时间复杂度O(n^2)，与边无关，适合求解边稠密的网的最小生成树。

    实现该算法需附设一个辅助数组closedge，以记录从 U 到 V-U 具有最小代价的边。对每个顶点 vi∈V-U，在辅助数组中存在一个相应分量closedge[i-1](下标从0开始)，它包括两个域。其中：lowcost存储该边上的权。显然，
   closedge[i-1].lowcost = Min{cost(u，vi)|u∈U}    即vi到已生成子树的最短距离等于到U中所有顶点中的最小边的权值。
   adjvex域存储该边依附的在U中的顶点。

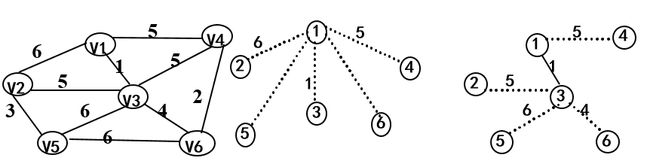
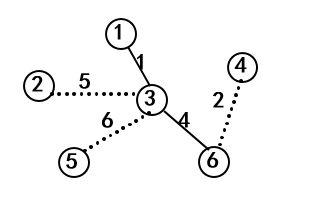
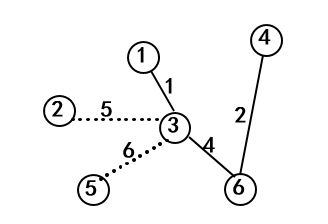
    示例：求下图最小生成树。假设开始顶点就选为顶点1，故有U={1}，V-U={2，3，4，5，6}

    

3.代码实现

3.1定义

#include<stdio.h>
//#include<stdlib.h>
/*
图的表示方法
DG（有向图）或者DN（有向网）：邻接矩阵、邻接表（逆邻接表--为求入度）、十字链表
UDG（无向图）或者UDN（无向网）：邻接矩阵、邻接表、邻接多重表
*/

//1.数组表示法（邻接矩阵）：将以有向网为例
#define INFINITY 32767//最大值：假定为无穷大
#define MAX_VERTEX_NUM 10//最大顶点数目
//typedef enum GraphKind {DG, DN, UDG, UDN};  //有向图：0，有向网：1，无向图：2，无向网：3

typedef int VRType;//顶点关系类型，对于无权图或网，用0或1表示相邻否；对于带权图或网，则为相应权值
typedef int VertexType;//顶点类型
typedef VRType AdjMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM];
typedef struct{
	VertexType vexs[MAX_VERTEX_NUM];//顶点向量
	AdjMatrix arcs;//邻接矩阵
	int vexnum, arcnum;//图的当前顶点数和弧数
	//GraphKind kind;//图的种类标志
}MGraph;//邻接矩阵表示的图


typedef struct{
	VertexType adjvex;
	VRType lowcost;
}closedge[MAX_VERTEX_NUM];//记录从顶点集U到V-U的代价最小的边的辅助数组
closedge close;

3.2邻接矩阵构造无向网G

//若图G中存在顶点v，则返回v在图中的位置信息，否则返回其他信息
int locateVex(MGraph G, VertexType v){
	for(int i = 0; i < G.vexnum; i++){
		if(G.vexs[i] == v)
			return i;
	}
	return -1;//图中没有该顶点
}

//采用邻接矩阵表示法构造无向网G
void createUDN(MGraph &G){
	printf("输入顶点数和弧数如:(5,3):");
	scanf("%d,%d", &G.vexnum, &G.arcnum);

	//构造顶点向量
	printf("输入%d个顶点（以空格隔开如：v1 v2 v3）:", G.vexnum);
	getchar();//吃掉换行符
	for(int m = 0; m < G.vexnum; m++){
		scanf("v%d", &G.vexs[m]);
		getchar();//吃掉空格符
	}

	
	//初始化邻接矩阵
	int i=0, j=0;
	for(i = 0; i < G.vexnum; i++){
		for(j = 0; j < G.vexnum; j++)
			G.arcs[i][j] = INFINITY;
	}

	//构造邻接矩阵
	VertexType v1, v2;//分别是一条弧的弧尾和弧头（起点和终点）
	VRType w;//对于无权图或网，用0或1表示相邻否；对于带权图或网，则为相应权值	
	printf("\n每行输入一条弧依附的顶点（先弧尾后弧头）和权值（如：v1 v2 3）:\n");
	fflush(stdin);//清除残余后，后面再读入时不会出错
	for(int k = 0; k < G.arcnum; k++){
		scanf("v%d v%d %d",&v1, &v2, &w);
		fflush(stdin);//清除残余后，后面再读入时不会出错
		i = locateVex(G, v1);
		j = locateVex(G, v2);
		G.arcs[i][j] = w;

		//又因为是无向网，所以邻接矩阵相对于对角线对称，所以还得对另外半边三角阵赋值！！！！！！！！！！重要
		G.arcs[j][i] = w;//重要！！！
	}
}

3.3Prim算法实现

int minimun(MGraph G, closedge close){
	int min = INFINITY;
	int min_i = -1;
	for(int i = 0; i < G.vexnum; i++){
		if(close[i].lowcost>0 && close[i].lowcost < min){
			min = close[i].lowcost;
			min_i = i;
		}
	}
	return min_i;//返回具有最小代价的边（u->vi）的vi的下标，即顶点vi的在图中的位置
}


//用prim算法从第u个顶点出发构造网G的最小生成树T，输出T的各个边，O（n^2）
void miniSpanTreePRIM(MGraph G, VertexType u){
	int k = locateVex(G, u);//找到顶点u在图中的位置
	//初始化辅助数组
	for(int i = 0; i < G.vexnum; i++){
		if(i != k){
			close[i].adjvex = k;
			close[i].lowcost = G.arcs[k][i];
		}
	}
	close[k].lowcost = 0;//初始时，U={u}

	for(i = 1; i < G.vexnum; i++){//选择其余的G.vexnum-1个顶点，每次选出一个，共需要选G.vexnum-1次
		k = minimun(G, close);//求出T的下一个结点：第k顶点
		printf("v%dv%d\n",G.vexs[close[k].adjvex], G.vexs[k]);//输出生成树的边(边起始点,边终点)
		close[k].lowcost = 0;//将第k顶点并入U集
		for(int j = 0; j < G.vexnum; j++){//由于U集有新顶点vk的并入，导致V-U里的各个顶点的lowcost的变化需要更新
			if(G.arcs[k][j] < close[j].lowcost){
				close[j].adjvex = k;
				close[j].lowcost = G.arcs[k][j];//重新选择最小代价边
			}
		}
	}
	printf("\n");
}

3.4.演示

/*测试：
6,10
v1 v2 v3 v4 v5 v6

v1,v2,6
v1,v3,1
v1,v4,5

v2,v3,5
v2,v5,3

v3,v4,5
v3,v5,6
v3,v6,4

v4,v6,2

v5,v6,6
*/
void main(){
	MGraph G;
	createUDN(G);	
	//printUDN(G);


	VertexType u;
	printf("请输入构造最小生成树的出发点：");
	scanf("v%d", &u);
	fflush(stdin);//清除残余后，后面再读入时不会出错
	miniSpanTreePRIM(G, u);

}