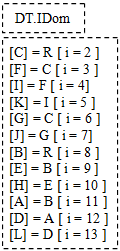dsa算法（16）

1.3.2.2.2.Lengauer-Tarjan算法第二、第三步

在174行，GraphTraits<FuncT*>::size(&F)返回F所代表的函数中的基本块的个数，但因为isPostDominator返回false，因此MultipleRoots维持为0。

 

Calculate（续）

 

172      // it might be thatsome blocks did not get a DFS number (e.g., blocks of

173      // infinite loops). In these cases an artificial exit nodeis required.

174      MultipleRoots|= (DT.isPostDominator() && N !=GraphTraits<FuncT*>::size(&F));

175   

176      // When naivelyimplemented, the Lengauer-Tarjan algorithm requires a separate

177      // bucket for each vertex. However, this is unnecessary,because each vertex

178      // is only placedinto a single bucket (that of its semidominator), and each

179      // vertex's bucketis processed before it is added to any bucket itself.

180      //

181      // Instead of usinga bucket per vertex, we use a single array Buckets that

182      // has two purposes. Before the vertex V with preordernumber i is processed,

183      // Buckets[i] stores the index of the firstelement in V's bucket. After V's

184      // bucket isprocessed, Buckets[i] stores the index of the next element in the

185      // bucketcontaining V, if any.

186      SmallVector<unsigned, 32> Buckets;

187      Buckets.resize(N + 1);

188      for (unsignedi = 1; i <= N; ++i)

189        Buckets[i] = i;

190   

191      for (unsignedi = N; i >= 2; --i) {

192        typenameGraphT::NodeType* W = DT.Vertex[i];

193        typenameDominatorTreeBase<typenameGraphT::NodeType>::InfoRec &WInfo =

194                                                                        DT.Info[W];

195   

196        // Step #2:Implicitly define the immediate dominator of vertices

197        for(unsigned j = i; Buckets[j] != i; j = Buckets[j]) {

198          typenameGraphT::NodeType* V = DT.Vertex[Buckets[j]];

199          typenameGraphT::NodeType* U = Eval<GraphT>(DT, V, i + 1);

200          DT.IDoms[V] = DT.Info[U].Semi < i ? U: W;

201        }

 

在Lengauer-Tarjan论文里原来使用bucket(w)保存半支配者为w节点的节点集合。这里做了改进，不再需要为每个节点保留一个集合，而是共用一个Buckets数组。理由是，首先每个节点只会放入一个bucket（因为其半支配者节点是唯一的）。更重要的是，bucket(v)中每个节点（即以v作为半支配者节点）都在v放入bucket之前得到处理。因此，这里所有的节点都共用一个Buckets，一开始Buckets与节点序号一一对应，而在处理过程中Buckets构成多个链，具有相同半支配者节点的节点通过某个链形成一个闭环。

192行的DT.Vertex[i]是第一步按深度优先遍历第i个访问到的节点，因此191行的循环是按降序进行第二、第三步计算。第二步的依据是Lengauer-Tarjan论文里的定理4。这个定理的内容是：

对于任何顶点w ≠ r，sdom(w) = min ({ v | (v, w) ∈ E且v < w } ∪ { sdom(u) | u > w且存在存在一条边(v,w)使得u*àv })（记法x*ày，表示x是y在伸展树中的一个祖先，E是边的集合）

第三步的依据则是论文中的推论1：假设w ≠ r，且v满足条件：在满足路径sdom(w)+à u*àw的u中，sdom(v)最小。那么

Calculate（续）

 

203        // Step #3:Calculate the semidominators of all vertices

204   

205        // initialize thesemi dominator to point to the parent node

206        WInfo.Semi = WInfo.Parent;

207        typedefGraphTraits<Inverse<NodeT> > InvTraits;

208        for (typename InvTraits::ChildIteratorType CI =

209             InvTraits::child_begin(W),

210             E = InvTraits::child_end(W); CI != E;++CI) {

211          typenameInvTraits::NodeType *N = *CI;

212          if (DT.Info.count(N)) {  // Only if thispredecessor is reachable!

213            unsigned SemiU = DT.Info[Eval<GraphT>(DT,N, i + 1)].Semi;

214            if (SemiU < WInfo.Semi)

215              WInfo.Semi = SemiU;

216          }

217        }

218   

219        // If V is anon-root vertex and sdom(V) = parent(V), then idom(V) is

220        // necessarilyparent(V). In this case, set idom(V) here and avoid placing

221        // V into abucket.

222        if (WInfo.Semi == WInfo.Parent) {

223          DT.IDoms[W] = DT.Vertex[WInfo.Parent];

224        } else {

225          Buckets[i] = Buckets[WInfo.Semi];

226          Buckets[WInfo.Semi] = i;

227        }

228      }

 

207行的GraphTraits<Inverse<NodeT>>就是GraphTraits<Inverse<const BasicBlock*> >，它是一个GraphTraits的特化类型。

 

296    template <> struct GraphTraits<Inverse<const BasicBlock*> > {

297      typedef const BasicBlock NodeType;

298      typedefconst_pred_iterator ChildIteratorType;

299      staticNodeType *getEntryNode(Inverse<constBasicBlock*> G) {

300        returnG.Graph;

301      }

302      static inline ChildIteratorType child_begin(NodeType *N) {

303        returnpred_begin(N);

304      }

305      static inline ChildIteratorType child_end(NodeType *N) {

306        returnpred_end(N);

307      }

308    };

 

在这个特化类型定义中，pred_begin与pred_end分别返回这样的迭代器：

 

89      inline const_pred_iteratorpred_begin(const BasicBlock *BB) {

90        returnconst_pred_iterator(BB);

91      }

93      inline const_pred_iterator pred_end(const BasicBlock *BB) {

94        returnconst_pred_iterator(BB, true);

95      }

 

迭代器const_pred_iterator的定义则是：

 

85      typedef PredIterator<const BasicBlock,

86                          Value::const_use_iterator> const_pred_iterator;

 

PredIterator定义的是节点前驱（Predecessor）迭代器。它接受两个模板参数，第一个是迭代对象，这里是BasicBlock* BB；第二个是该对象真正使用的迭代器，这里是Value::const_use_iterator，即value_use_iterator<constUser>。

 

47        explicit inline PredIterator(Ptr*bb) : It(bb->use_begin()) {

48          advancePastNonTerminators();

49        }

 

47行的use_begin返回指向定义使用链（def-uselist）开头的迭代器，对于BasicBlock其定义使用链的内容就是其前驱节点（即前驱与该BasicBlock构成图中的一条边）。

显然上面208行的循环是遍历192行的w节点的前驱。212行确认指定的前驱节点在深度优先遍历中被访问到了。对于这个前驱节点v，通过下面的函数Eval执行如下操作：

如果v是森林中一棵树的根节点，就返回v。否则，假设r是森林中包含v的树的根节点。返回在路径r*àv上的节点u，满足u ≠ r，且semi(u) 最小。而这个森林则包含顶点集V及（树）边集合 { (parent(w), w) | 顶点w已经被处理 }。

 

106    template<classGraphT>

107    typename GraphT::NodeType*

108    Eval(DominatorTreeBase<typename GraphT::NodeType>& DT,

109         typenameGraphT::NodeType *VIn, unsigned LastLinked) {

110      typenameDominatorTreeBase<typenameGraphT::NodeType>::InfoRec &VInInfo =

111                                                                      DT.Info[VIn];

112      if (VInInfo.DFSNum < LastLinked)

113        return VIn;

114   

115      SmallVector<typenameGraphT::NodeType*, 32> Work;

116      SmallPtrSet<typenameGraphT::NodeType*, 32> Visited;

117   

118      if (VInInfo.Parent >= LastLinked)

119        Work.push_back(VIn);

120     

121      while(!Work.empty()) {

122        typenameGraphT::NodeType* V = Work.back();

123        typenameDominatorTreeBase<typenameGraphT::NodeType>::InfoRec &VInfo =

124                                                                         DT.Info[V];

125        typenameGraphT::NodeType* VAncestor = DT.Vertex[VInfo.Parent];

126   

127        // ProcessAncestor first

128        if (Visited.insert(VAncestor) &&VInfo.Parent >= LastLinked) {

129          Work.push_back(VAncestor);

130          continue;

131        }

132        Work.pop_back();

133   

134        // Update VInfobased on Ancestor info

135        if (VInfo.Parent < LastLinked)

136          continue;

137   

138        typenameDominatorTreeBase<typenameGraphT::NodeType>::InfoRec &VAInfo =

139                                                                DT.Info[VAncestor];

140        typenameGraphT::NodeType* VAncestorLabel = VAInfo.Label;

141        typenameGraphT::NodeType* VLabel = VInfo.Label;

142        if (DT.Info[VAncestorLabel].Semi < DT.Info[VLabel].Semi)

143          VInfo.Label = VAncestorLabel;

144        VInfo.Parent = VAInfo.Parent;

145      }

146   

147      returnVInInfo.Label;

148    }

 

我们用个例子来观察上面的代码，这个例子来自Lengauer-Tarjan论文。它是这样一个图，实线组成的是该图深度优先遍历的伸展树，虚线是非树边。

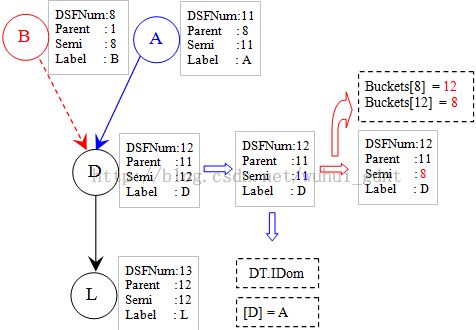
这棵树一共有13个节点，上面191行的循环从序号最大的叶子节点开始，以序号的倒序遍历树节点。循环第一遍时处理节点L，其前驱是D，L同时是所在子树的根节点：

这时森林只包含[D, L]两个节点，及一条路径(D, L)，而D是子树D->L的根节点。

循环i = 12时，处理节点D，其前驱是A和B。在处理前驱B时，由于D的semi被更新为8，其序号被放入Buckets[8]中，这时Buckets[8]->Buckets[12]->Buckets[8]构成一个闭环。

循环i = 11时，处理节点A，其前驱是B和R。处理B时森林只有一棵树，由节点A，B，D和L组成，处理R时森林由两棵子树组成，一棵与处理B时相同，另一棵则只包含节点R。因为现在A的semi是1，因此它的序号被放入Buckets[1]。这时Buckets[1]->Buckets[11]->Buckets[1]构成闭环。

循环i = 10时，处理节点H，其前驱是E和L。注意节点L所在的（森林中）树。Eval将L的Label，Parent及Semi都设得与A一致，这在Lengauer-Tarjan算法中称为路径压缩（我们只要访问L，就知道B->L这棵树上具有最小semi的节点）。因为现在H的semi是1，因此它的序号被放入Buckets[1]。这时Buckets[1]->Buckets[10]->Buckets[11]->Buckets[1]构成闭环。

在循环i = 9时，处理节点E，其前驱是B和H。这个时候森林中有节点[B, A, D, L, H]，构成一棵具有边B->A，A->D，D->L，B->E，E->H的树。由于路径压缩的缘故，H给出了这棵子树中，除根节点外最小的semi值。因为现在E的semi是1，因此它的序号也放入Buckets[1]，Buckets[1]->Buckets[9]->Buckets[10]->Buckets[11]->Buckets[1]构成闭环。

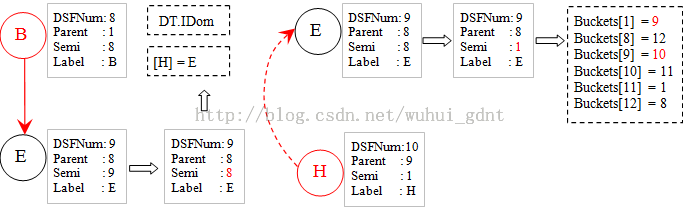
在循环i = 8时，处理节点B，其前驱是R。但因为这时Buckets[8]不是8，因此197行的循环将处理Buckets[8]，Buckets[12]，这两个都是semi（暂定）为8的节点。注释中写错了，这实际上对应Lengauer-Tarjan算法的第三步，而第二步才是第三步。

目前的森林是以B为根节点的子树，由于路径压缩的缘故，D的Parent现在是B。Eval的作用是返回节点所在子树中具有最小semi的节点——这里是A，这正是D节点Label中的内容。不过这两次处理都没有改变任何东西。

在循环i = 7时，处理节点J，其前驱是G，它是所在（森林中的）子树的根节点，这个处理很简单。

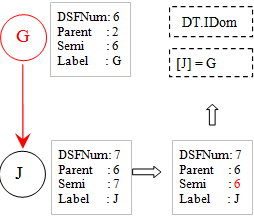
在循环i = 6时，处理节点G，其前驱是C，它是所在（森林中的）子树的根节点，这个处理同样简单。

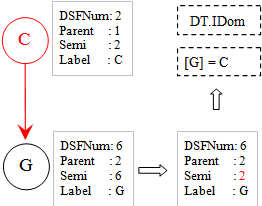
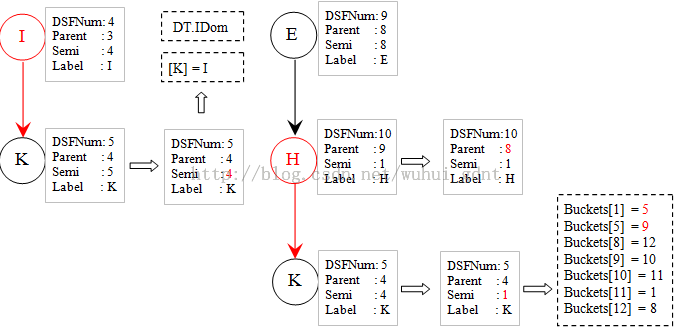
在循环i = 5时，处理节点K，其前驱是I，及H。

由于H节点的传播，K节点的Semi变成1，这样Buckets[1]-> Buckets[5]-> Buckets[9]-> Buckets[10]-> Buckets[11]->Buckets[1]构成新的闭环。

在循环i = 4时，处理节点I，其前驱是F，G，J及K。其中G与J对I没有任何影响。

Buckets[1]->Buckets[4]->Buckets[5]->Buckets[9]->Buckets[10]->Buckets[11]->Buckets[1]构成新的闭环。

在循环i = 3时，处理节点F，其前驱是C。结果是：

类似的，在循环i = 2时，处理节点C，其前驱是B。

至此，我们完成了Lengauer-Tarjan算法的前三步。得到如下所示的图。

而DT.IDoms中的内容则如下图所示：

Calculate（续）

 

230      if (N >= 1) {

231        typenameGraphT::NodeType* Root = DT.Vertex[1];

232        for(unsigned j = 1; Buckets[j] != 1; j = Buckets[j]) {

233          typenameGraphT::NodeType* V = DT.Vertex[Buckets[j]];

234          DT.IDoms[V] = Root;

235        }

236      }

 

接下来在230行，遍历Buckets中Semi为1的节点，把它们的直接支配者设置为根节点。因此对我们的例子，DT.IDoms变为：