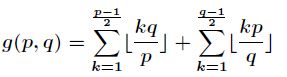地大校赛2014 题解
比赛地址
中国地质大学(北京)第八届程序设计竞赛现场决赛
CUGB的ACM公网ip已申请下来,他们的新OJ就不透露了,本文代码是赛后重写的,没有拿到现场的程序。
A. 部落战争
题意:
有一个部落,每天能生产x金币,周末加倍;每天能掠夺y金币,周末不加倍。给定起始的天是星期几,求获得n金币需要多少天,那天星期几。
x, y, n <= 10 ^ 7。
题解:
对每一天的情况去模拟,直到达到目的。时间复杂度O(n/(x+y))。
代码:
#include <cstdio>
int n, x, y, w, now, day;
int main()
{
while(scanf("%d%d%d%d", &n, &x, &y, &w) == 4)
{
now = day = 0;
while(1)
{
now += x + y;
if(w >= 6)
now += x;
++day;
if(now >= n)
break;
++w;
if(w > 7)
w = 1;
}
printf("%d %d\n", day, w);
}
return 0;
}
B. 影分身之术
题意:
给定n,对其分解质因数,求质因数出现的次数和,并升序输出每个质因数,每个质因数输出出现的次数次。t组数据。
t <= 10 ^ 5, n <= 5 * 10 ^ 6。
题解:
在1 ~ \sqrt{n}内分解质因数(因为一个大于\sqrt{n}的因子一定对应一个小于\sqrt{n}的因子),存下来,输出个数再输出每个质因数即可。
时间复杂度O(t\sqrt{n}),质因子个数不超过logn个。
代码:
#include <cstdio>
int t, n, a[23333];
int main()
{
scanf("%d", &t);
while(t--)
{
scanf("%d", &n);
a[0] = 0;
for(int i = 2; i * i <= n; ++i)
while(n % i == 0)
{
a[++a[0]] = i;
n /= i;
}
if(n > 1)
a[++a[0]] = n;
printf("%d\n", a[0]);
for(int i = 1; i < a[0]; ++i)
printf("%d ", a[i]);
printf("%d\n", a[a[0]]);
}
return 0;
}
C. 黄焖鸡与矩阵
题意:
给定一个由n * m方格组成的矩形,每次可以沿着方格的边缘水平或竖直地切割。求切割k次之后分成的最小的矩形最大由多少个方格组成。
n, m < 10 ^ 9, k < 2 * 10 ^ 9。
题解:
设横着切x次,则纵着切k - x次,根据抽屉原理可知答案是[n / (x + 1)] + [m / (k - x + 1)],注意到左边的式子只有\sqrt{n}个值,对于一个值可以求出最大的x使得右边尽量大。时间复杂度O(\sqrt{n})。
后来被出题人的题解虐掉了,出题人直接贪心:最优解一定尽可能只横着分割,或只竖着分割,因为要是横竖交叉的肯定会使分得矩阵数量增加,从而使得矩阵变小,得不到最优解。
首先不妨假设n <= m。
当k > m - 1时,只能横竖交叉分割,那么先尽可能横着划分m - 1次,然后剩余的k - m + 1次去竖着分割,答案为[n / (k - m + 2)]。
当n - 1 < k <= m - 1时,只用横着分割k次,答案为[m / (k + 1) * n]。
当k <= n - 1时,横着分割或是竖着分割均可能为最优解,答案为max{[m / (k + 1) * n], [n / (k + 1) * m]}。
时间复杂度O(1)。
代码:
#include <cstdio>
#include <algorithm>
using namespace std;
typedef long long LL;
LL n, m, k, ans;
int main()
{
while(scanf("%lld%lld%lld", &n, &m, &k) == 3)
{
if(k > n + m - 2)
{
puts("fz is so clever");
continue;
}
if(n < m)
swap(n, m);
if(k > n - 1)
ans = m / (k - n + 2);
else
ans = max(n / (k + 1) * m, m / (k + 1) * n);
printf("%lld\n", ans);
}
return 0;
}
D. IOCCC情书生成器
题意:
给定一个IOCCC情书生成器代码的样本,给定密码表,给定一个字符串作为情书,输出相应的IOCCC情书生成器代码。
字符串长度 <= 84。
题解:
按照样本模拟一遍就好了。时间复杂度O(84)。似乎Special Judge会修改输入流,所以不能写多组输入。
代码:
#include <cstdio>
#include <cstring>
const char *tran = "(fnm:qeb)jcr,[<*ak>+3g.d1-?h^i_=", *pos = "abcdefghijklmnopqrstuvwxyz ,.\'!?", *unuse = "stuvwxyz{|}~!#";
char tem[2333] = "\
#include <stdio.h>\n\
main(t ,_,a) char*a;{return\n\
t<1?main(*a,a[-t],\"=a-1kj3gnm:q\\\n\
ebh_cf*<r.d>i^+?,()[?qzyrjuvcdefg\\\n\
h,!kbpolwxs'.t main(\")&&a[-t]&&main\n\
(t-1,_,a):t/2?_==*a?putchar(32[a])\n\
:_%115<36||main(t,_,a+1):main(\n\
0,t,\"````````````````````\\\n\
`````````````````````\\\n\
`````````````````\\\n\
`````````````\\\n\
`````````\\\n\
````\")\n\
;}";
char str[100], out[2333];
char trans(char x)
{
for(int i = 0; pos[i] != '\0'; ++i)
if(x == pos[i])
return tran[i];
return unuse[0];
}
int main()
{
gets(str);
for(int i = 0; i < 84; ++i)
str[i] = trans(str[i]);
memcpy(out, tem, sizeof tem);
for(int i = 0, j = 0; out[i] != '\0'; ++i)
if(out[i] == '`')
out[i] = str[j++];
printf("%s", out);
return 0;
}
E. SIO__Five的滑板鞋
题意:
1 < p, q < 4294967296。
题解:
如果p和q互质(即p ≠ q),那么直线y = p * x / q,在[1, (q - 1) / 2]之间没有经过一个整点,所求即为该直线上方与下方的整点在一个矩形内的个数。
否则p = q,所求化为(p ^ 2 - 1) / 4。
时间复杂度O(1)。
代码:
#include <cstdio>
long long p, q;
int main()
{
while(scanf("%lld%lld", &p, &q) == 2)
{
if(p == q)
p += 2;
p = p - 1 >> 1;
q = q - 1 >> 1;
printf("%lld\n", p * q);
}
return 0;
}
F. SIO__Five的礼物
题意:
有2n个浮点数,做n次操作,每次操作从2n个浮点数里选没操作过的两个数,一个取上整,一个取下整。求得到的2n个整数之和与原来2n个浮点数之和的差的最小值。t组数据。
t <= 100, n <= 2000。
题解:
取上整和取下整相差只有1,所以所有的数取下整,求出当前的差,统计有多少个数还可以取上整(实际不得超过n个),再考虑得到的最小的差。
时间复杂度O(tn)。
代码:
#include <cmath>
#include <cstdio>
#include <algorithm>
using namespace std;
const double eps = 1e-8;
int t, n, m;
double x, sum;
int main()
{
scanf("%d", &t);
while(t--)
{
m = 0;
sum = 0;
scanf("%d", &n);
for(int i = 0; i < n << 1; ++i)
{
scanf("%lf", &x);
x -= (int)x;
if(x > eps)
{
sum += x;
}
else
++m;
}
if(m < n)
sum -= n - m;
else
m = n;
while(sum - 1 > eps && m)
{
sum -= 1;
--m;
}
if(m && abs(sum - 1) < sum)
sum = abs(sum - 1);
printf("%.3f\n", abs(sum) + eps);
}
return 0;
}
G. Ant、本子与粉碎机
题意:
给定n个物品,每个物品有两个属性l和w,现在要用一些机器销毁物品。
一台机器可以销毁一些物品,但是这些物品必须有序的排列,而且前一项的l和w都不小于后一项的l和w。
求最少需要多少台机器。t组数据。
t <= 30, n <= 5 * 10 ^ 4, l, w <= 10 ^ 5。
题解:
可以先对一个属性l进行升序排序,对于l相同的物品再按照w进行升序排序,这样我们可以想到dp求出一个机器最多销毁的物品数,即新序列的w的最长不下降子序列,题目要求最少机器个数,则为新序列的w的最长上升子序列的长度。
若设f[i]表示以第i个物品结尾的w的最长上升子序列的长度,g[k]表示满足f[i] = k的最小的a[i].w的值,则可以证明g数组的值是单调的,在计算f[i]时可以在g数组上二分查找最大的满足g[k] < a[i].w的下标k,则f[i] = k + 1。
时间复杂度O(nlogn)。
代码:
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int maxn = (int)6e4;
int t, n, g[maxn], ans;
struct Node
{
int l, w;
bool operator < (const Node &x) const
{
return l < x.l || l == x.l && w < x.w;
}
} a[maxn];
int BinarySearch(int l, int r, int val)
{
while(l < r)
{
int m = l + r >> 1;
if(g[m] <= val)
r = m;
else
l = m + 1;
}
return l;
}
int main()
{
scanf("%d", &t);
while(t--)
{
ans = 0;
memset(g, 0, sizeof g);
scanf("%d", &n);
for(int i = 1; i <= n; ++i)
scanf("%d%d", &a[i].l, &a[i].w);
sort(a + 1, a + n + 1);
for(int i = 1; i <= n; ++i)
{
int k = BinarySearch(1, n, a[i].w);
g[k] = max(g[k], a[i].w);
ans = max(ans, k);
}
printf("%d\n", ans);
}
return 0;
}
H. 世界统一
题意:
给定两棵无根树,点数分别为n和q,边权均为1。
现在从两颗树里随机各取一点将其连接,求合并后的树上最远两点距离的期望。t组数据。
t <= 10, n, q <= 4 * 10 ^ 4。
题解:
对于一棵树,可以利用树型dp求出每点到最远点的路径长度,记题目中两个树的对应值为f1[], f2[]。
做两次树形dp的方法需要记录的值有某点子树里到某点的最远点、次远点的路径长度,全树里到某点的最远点、次元点的路径长度。树形dp的时间复杂度为O(n)。
现在考虑左边第i个点与右边第j个点连接后的情况,最远距离是原来两棵树里的最远距离和现在f1[i] + f2[j] + 1的最大值,直接统计是O(n^2)的。
学长考虑的是使用fft快速算卷积,官方题解是对f2[]排序,枚举f1[]二分查找f2[]算入答案的区间,时间复杂度均为O(nlogn)。实际上也可以O(n)来做。
考虑将两边算出来的最远距离f1[], f2[]排个升序,对于一个f1[i],最远距离是f1[i] + f2[j] + 1的情况是连续的一段f2[j],可以记录前缀和。考虑比i大的i'对应的情况,新的满足最远距离是f1[i'] + f2[j'] + 1的情况还是连续的一段f2[j']且j'不大于j,则可以通过枚举i,利用单调性再枚举j来计算这种情况,随着i的递增j是递减的,最多减n次,时间复杂度O(n),最远距离为两棵树原来的直径的情况很好统计这里不赘述。
代码:#include <vector>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const double eps = 1e-5;
const int maxn = (int)1e6;
int n, q, f[maxn], g[maxn], ff[maxn], pos[maxn], maxl;
long long sg[maxn], ans;
bool vis[maxn];
vector<int> e[maxn];
void dfs1(int u)
{
vis[u] = 1;
for(int i = 0, j = (int)e[u].size(); i < j; ++i)
{
int &v = e[u][i];
if(vis[v])
continue;
dfs1(v);
if(f[u] < f[v] + 1)
{
pos[u] = v;
ff[u] = f[u];
f[u] = f[v] + 1;
}
else if(ff[u] < f[v] + 1)
ff[u] = f[v] + 1;
}
}
void dfs2(int u)
{
vis[u] = 1;
for(int i = 0, j = (int)e[u].size(); i < j; ++i)
{
int &v = e[u][i];
if(vis[v])
continue;
int &w = pos[u] == v ? ff[u] : f[u];
if(f[v] < w + 1)
{
pos[v] = u;
ff[v] = f[v];
f[v] = w + 1;
}
else if(ff[v] < w + 1)
ff[v] = w + 1;
dfs2(v);
}
}
int dp()
{
for(int i = 1; i <= n; ++i)
e[i].clear();
for(int i = 1; i < n; ++i)
{
int u, v;
scanf("%d%d", &u, &v);
e[u].push_back(v);
e[v].push_back(u);
}
memset(f, 0, sizeof f);
memset(ff, 0, sizeof ff);
memset(pos, 0, sizeof pos);
memset(vis, 0, sizeof vis);
dfs1(1);
memset(vis, 0, sizeof vis);
dfs2(1);
sort(f + 1, f + n + 1);
return f[n];
}
int main()
{
while(scanf("%d%d", &n, &q) == 2)
{
ans = 0;
memset(sg, 0, sizeof sg);
maxl = dp();
swap(n, q);
memcpy(g, f, sizeof f);
maxl = max(maxl, dp());
for(int i = q; i; --i)
sg[i] = sg[i + 1] + g[i];
for(int i = 1, j = q; i <= n; ++i)
{
while(j && f[i] + g[j] + 1 >= maxl)
--j;
ans += (f[i] + 1) * (q - j) + sg[j + 1];
ans += maxl * j;
}
printf("%.3f\n", (double)ans / (n * q) + eps);
}
return 0;
}
I. MaoMao、奶牛和牧场
题意:
给定一个n点m边的无向图,求最少需要添几条边可以使得任意两点间至少有两条边不重复的路径。
n <= 6000, m <= 10000。
题解:
这个就是真的裸题了。任意两点间至少有两条边不重复的路径的连通分量称为边-双连通分量,可以利用tarjan算法算出桥,再做一遍dfs求出所有的边-双连通分量。
如果将连通分量缩为一个“点”,则新图为一颗树,树边为原图的桥,现在可以利用贪心的思路,每个度数为1的点都可以与另一个度数为1的点连边,使其缩成一个边-连通分量,则可以归纳得出答案为[(度数为1的点数 + 1) / 2]。
时间复杂度O(n + m)。
代码:
#include <cstdio>
#include <cstring>
const int maxn = 6666, maxm = 23333;
struct Edge
{
int v, nxt;
} e[maxm];
int t, n, m, tot, lnk[maxn], pre[maxn], cnt, bcc[maxn], d[maxn], ans;
bool used[maxm];
int tarjan(int u, int Fa)
{
int lowu = pre[u] = ++tot;
for(int it = lnk[u]; it != -1; it = e[it].nxt)
{
if(Fa == (it ^ 1))
continue;
int &v = e[it].v;
if(!pre[v])
{
int lowv = tarjan(v, it);
if(lowu > lowv)
lowu = lowv;
if(pre[u] < lowv)
used[it] = used[it ^ 1] = 1;
}
else if(lowu > pre[v])
lowu = pre[v];
}
return lowu;
}
void dfs(int u)
{
bcc[u] = cnt;
for(int it = lnk[u]; it != -1; it = e[it].nxt)
if(!used[it] && !bcc[e[it].v])
dfs(e[it].v);
}
int main()
{
scanf("%d", &t);
while(t--)
{
scanf("%d%d", &n, &m);
ans = tot = cnt = 0;
memset(d, 0, sizeof d);
memset(pre, 0, sizeof pre);
memset(bcc, 0, sizeof bcc);
memset(lnk, -1, sizeof lnk);
memset(used, 0, sizeof used);
while(m--)
{
int u, v;
scanf("%d%d", &u, &v);
e[tot] = (Edge){v, lnk[u]};
lnk[u] = tot++;
e[tot] = (Edge){u, lnk[v]};
lnk[v] = tot++;
}
tot = 0;
tarjan(1, -1);
for(int i = 1; i <= n; ++i)
if(!bcc[i])
{
++cnt;
dfs(i);
}
for(int u = 1; u <= n; ++u)
for(int it = lnk[u]; it != -1; it = e[it].nxt)
if(bcc[u] != bcc[e[it].v])
++d[bcc[u]];
for(int i = 1; i <= cnt; ++i)
if(d[i] == 1)
++ans;
printf("%d\n", ans + 1 >> 1);
}
return 0;
}
J. 无聊的Bright
题意:
给定一个正整数n,现在有n个砝码,每个砝码依次贴着1~n,表示重量是1g~ng,问最少需要用天平称多少次才能确定标号为i的砝码重量一定为ig。
n < 15。
题解:
结论题。来自UyHiP趣题“用最少的称重次数验证硬币的重量”,Matrix67在其Blog中有提到这个趣题。
答案为著名的数列,Baron Munchhausen's Omni-Sequence,oeis A186313,当前人们也只是确定了前几十项的结果。
代码:
#include <cstdio>
const int Baron[] = {0, 0, 1, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 3, 3, 3};
//oeis A186313 Baron Munchhausen's Omni-Sequence.
int t, n;
int main()
{
scanf("%d", &t);
while(t--)
{
scanf("%d", &n);
printf("%d\n", Baron[n]);
}
return 0;
}
小记
做题顺序是ABGED,这是第一次参加ACM现场赛,有些紧张。做A时看到数据范围达到10 ^ 7结果浪费时间去写了O(n / 7)的算法,不值得。做C的时候RE,TLE,有些心烦。做D的时候经常PE,不知为何,最后Accepted了。做E的时候是打表看出来的,之前以为WA在了爆long long,浪费时间写了高精度,实际是有多组数据,题目没有说清。做H的时候已经写好了树形dp但是一直WA到了比赛结束。看着J就没有写的欲望,需要多读读书。第一次现场赛,Rank9,因为罚时。比赛难度整体高于北师大新生赛,低于北航校赛,适合学习算法。