不共线三点确定特征平面并求解平面系数

1.基本原理

 已知三点p1,p2,p3,求其平面方程，p1=[x1,y1,z1];p2=[x2,y2,z2];p3=[x3,y3,z3];那么求解下面矩阵q行列式就是了：q=[ones(4,1),[x,y,z];p1;p2;p3];detb=det(q);最后令q=0;

这里的求解方法是四阶矩阵的行列式求解，可以从三阶矩阵的行列式推导出来，那就是常规的求解方法：方程组写成[p1;p2;p3]=D,其中D=[d,d,d]'表示平面方程的常数项，先求q=[p1;p2;p3]的行列式，再分别求D与三个坐标两个分量合成的三阶矩阵的行列式，设为q1,q2,q3；那么所求的平面方程的四个参数就是A=q1/q;B=q2/q;c=q3/q;D=d;同时乘以q/d所得结果本质上就是上面四阶矩阵行列式解。

2.Matlab代码

<span style="font-size:14px;">function [a,b,c,d] = TriPts2Plane( A,B,C )
%不共线三点确定一个平面
%具体指，2DUS提供的数据点确定3DCT中的一个参考平面
% A,B,C 不共线的三个点
%a,b,c,d 确定平面方程的参数
%沈春旭/沈子恒 2016.4.8
%-------------------------------Step1:确定平面方程-------------------------%
    syms x y z
%D的行列式等于零就是平面方程。
if (det([A;B;C]) == 0)
    msgbox('特征点线性相关，不足以构成平面');
    return;
else
    D=[ones(4,1),[[x,y,z];A;B;C]];
    detd = det(D);
    str = char(detd);
%---------------------------------Step2: 提取系数--------------------------%
    amark = find(str=='x');
    bmark = find(str=='y');
    cmark = find(str=='z');
%------------------------------------------- 
    if(size(amark,2))
        a = coeffs(detd,x);   a = double(a(2));%系数按照升幂顺序排列
    else
        a = 0;
    end
%------------------------------------------- 
    if(size(bmark,2))
        b = coeffs(detd,y);   b = double(b(2)); 
    else
        b = 0;
    end
%------------------------------------------- 
    if(size(cmark,2))
        c = coeffs(detd,z);   c = double(c(2)); 
    else
        c = 0;
    end
%------------------------------------------- 
[~,num] = size(str);
    if(num>max([amark,bmark,cmark]))
        d = coeffs(detd);     d = double(d(1));
    else
        d = 0;
    end
%-------------------------------------------    
end
end</span>

测试代码：

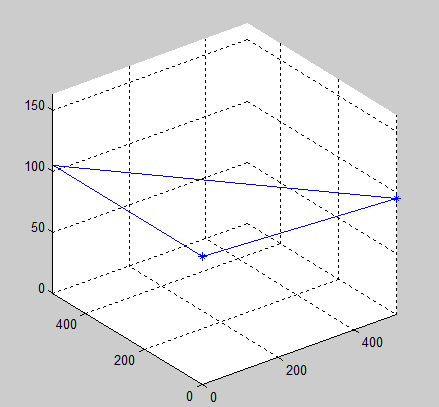
clc; clear all; close all;
A=[0,0,105];%A,B,C的坐标由自己定义。
B=[0,512,105];
C=[512,0,95];
[a,b,c,d]=TriPts2Plane(A,B,C);
plane = [A;B;C;A];
plot3(plane(:,1),plane(:,2),plane(:,3),'*');
hold on
%ezmesh(z)plot3(plane(:,1),plane(:,2),plane(:,3),'b-');
axis([0 512 0 512 0 163])
grid on;

测试结果：