机器学习day13 机器学习实战线性回归
这两天学习了回归的相关知识,后面本来有个实战案例,但无奈不能上网站抓取信息不能实现,还有一个缩减的方法前向逐步回归没有看,lasso的简化版,只看了岭回归。
回归与分类的区别:回归的标签值为连续的数值,我们做的是预测未知点的标签数值,分类的标签值为类别,我们做的是预测其他样本的分类。
相关系数的计算:
有柯西不等式可以得到相关系数的绝对值|r| < 1。-1 < r < 1,r越趋近1或-1相关性越大,越能用直线表示,r > 0说明x,y同增,r < 0说明x,y同减。
直线y = wx。截距为x0 * w0 ,x0不是特性,设为1.0。
衡量一个拟合直线的标准是计算所有点与直线y值之差的平方之和,
对求导得
这里要求矩阵的逆,矩阵的逆不一定会有,矩阵逆的充分必要条件是矩阵的行列式不为0,numpy中有函数实现linalg.det()。求矩阵的逆numpy也有相应函数。
后面会写一些相关细节。
step1:
读取简单数据:
#读取简单数据
def loadDataSet(filename):
featruenum = len(open(filename).readline().split('\t')) - 1
dataset = []
lavels = []
f = open(filename)
for i in f.readlines():
line = []
l = i.strip().split('\t')
for j in range(featruenum):
line.append(float(l[j]))
dataset.append(line)
lavels.append(float(l[-1]))
return dataset, lavelsstep2:
可视化数据集中的点:
#画出ex0的数据点
def drawPoint(dataset, lavels):
xtemp = array(dataset)
xx = xtemp[ : , 1]
yy = array(lavels)
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(xx, yy, s = 15, c = 'green')
fig.show()
可以看到点基本上分布呈直线状,我们似乎能找到一条直线大致拟合这些数据。
step3:
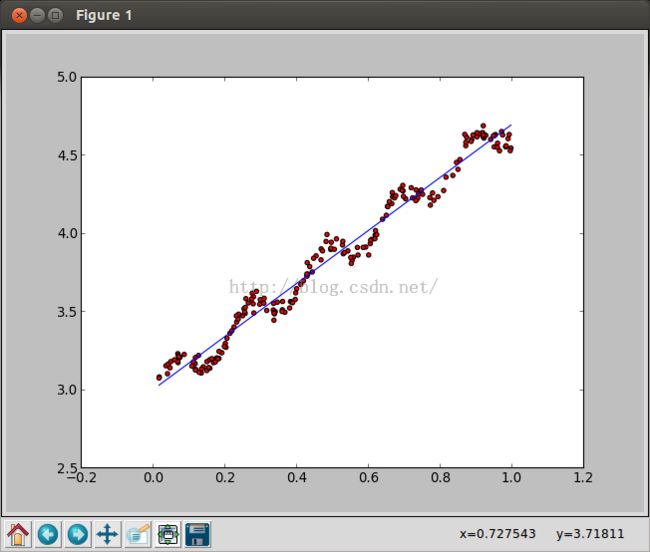
最小二乘法计算最佳系数,并画出拟合直线。
#最小二乘法计算w
def getW(x, y):
xmat = mat(x)
ymat = mat(y).T
xT = xmat.T
tempx = xT * xmat
if linalg.det(tempx) == 0.0:
print "error"
return
w = tempx.I * xT * ymat
return w
#画出线性拟合直线
def drawBestLine(x, y, w):
tempx = array(x)
tempy = array(y)
xx = tempx[ : , 1]
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(xx, tempy, s = 15, c = 'red')
xx.sort(0)
tempy = tempx * w
ax.plot(xx, tempy)
fig.show()
这条拟合直线为:
可以看出拟合的效果令人满意。
但是我们还可以挖掘出一点数据的潜在价值,即让拟合线更加贴近数据,不一定是直线。
我们引入了局部加权线性回归,简称LWLR。
根据测试点和训练集中数据的距离给训练集数据设定不一样的权值,离测试点近的训练点权值高,起到的作用更大。
权值采取高斯核,公式在这里不给出。有两个方面会影响权值,一为距离,二为k值,k越大距离测试点相同距离的点权值越大,也就是k越大,影响最终拟合线的点越多,越倾向线性回归,k越小,影响最终拟合线的点越少,越形成小局部的点拟合一条线,很多局部最终会合成一条拟合度很高的曲线,这样会过拟合,未必好。
我们接下来设置3个不同的k来看一下这种区别。
step4:
LWLR的方法给出3条不同k的拟合线:
#局部加权线性回归(对单个数据预测)
def LWLR(data, l, t, k = 1.0):
test = mat(t)
datamat = mat(data)
lavelsmat = mat(l).T
m = shape(datamat)[0]
w = mat(eye((m)))
for i in range(m):
diffmat = datamat[i] - test
w[i, i] = exp(diffmat * diffmat.T/(-2.0 * k ** 2))
tempmat = datamat.T * (w * datamat)
if linalg.det(tempmat) == 0.0:
print 'error'
return
weights = tempmat.I * datamat.T * w * lavelsmat
return test * weights
#对数据集LWLR
def testLWLR(data, l, testdata, k = 1.0):
m = shape(testdata)[0]
ymat = zeros(m)
for i in range(m):
ymat[i] = LWLR(data, l, testdata[i], k)
return ymat
#绘制LWLR拟合的回归线(不一定是直线)
def drawLWLR(d, lavel, k):
data = array(d)
l = array(lavel)
tempx = data[ : , 1]
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(tempx, l, s = 15, c = 'red')
temp = data.copy()
temp.sort(0)
tempy = testLWLR(data, l, temp, k)
ax.plot(temp[ : , 1], tempy)
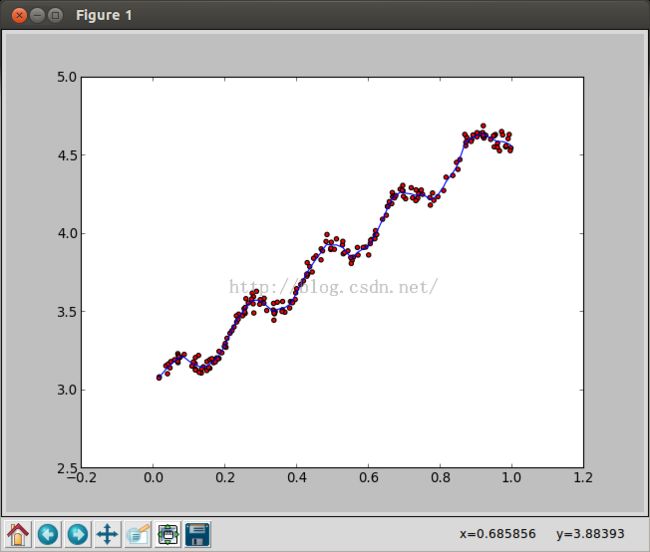
plt.show()k = 1时的拟合线:
k = 0.01的拟合线,已经是一条比较平滑的曲线了:
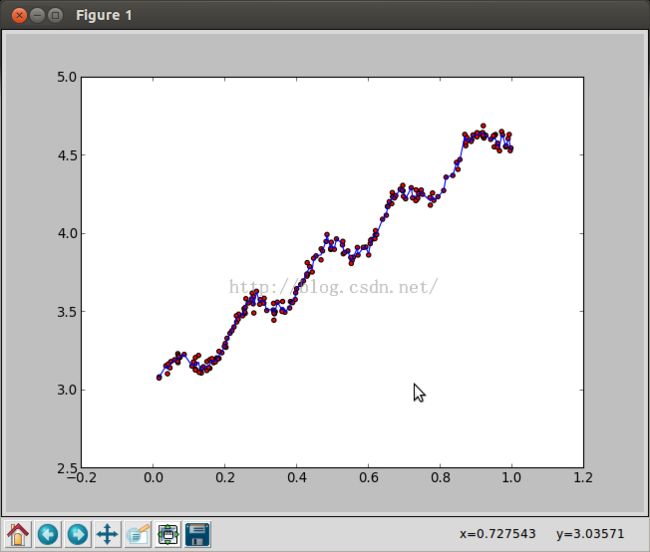
k = 0.003的拟合线,已经惨不忍睹了,虽然对训练数据拟合的很好:
我们看到了上面两种线性回归方式,但是有个特殊的情况,就是当特征数大于样本数的时候无法求矩阵的逆,也就无法应用上面的两种方法,下面介绍一种新方法:岭回归。
岭回归可以处理这种情况,公式类似于LWLR,公式参见《机器学习实战》。公式添加了一个我们自行设置的系数,我们采取了30个不同的值来观察一下w的改变。
step5:
岭回归:
#岭回归
def ridgeRegression(data, l):
xmat = mat(data)
ymat = mat(l).T
ymean = mean(ymat, 0)
ymat = ymat - ymean
xmean = mean(xmat, 0)
v = var(xmat)
xmat = (xmat - xmean) / v
#取30次不同lam岭回归的w
cycle = 30
wmat = zeros((cycle, shape(xmat)[1]))
for i in range(cycle):
tempw = ridgeGetW(xmat, ymat, exp(i - 10))
wmat[i, : ] = tempw.T
return wmat
#计算岭回归的w
def ridgeGetW(x, y, lam = 0.2):
tempx = x.T * x
temp = tempx + lam * eye(shape(x)[1])
if linalg.det(temp) == 0.0:
print 'error'
return
w = temp.I * x.T * y
return w
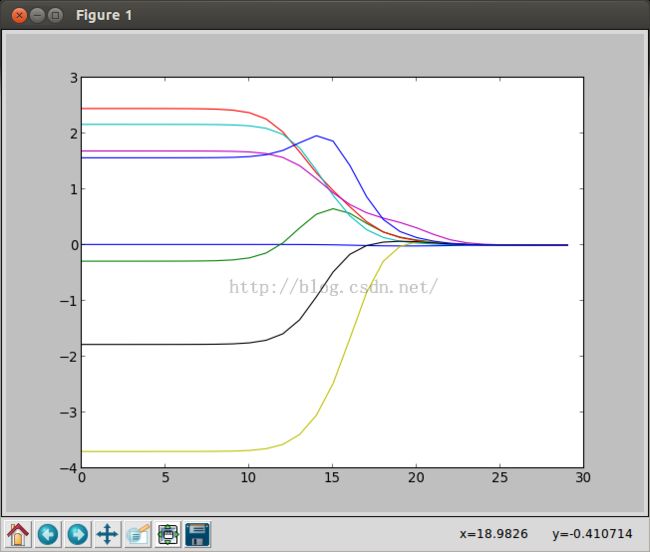
30次计算不同的权值之后我们可视化一下这些权值:
横坐标是我们设置的值的log值,当我们设置的值很小的时候,结果和线性回归的w差不多,但是我们设置的值比较大时,w会慢慢变成0,起不到任何作用,干扰了我们的拟合。
我们也可以通过这张图发现那些特性影响预测值大,那些影响预测值小,也可以摒弃一些权值小的特性,便于后面处理。
这就是回归的基本知识,有个前向逐步回归和lasso没有看,案例因为没能连接上网站没能进行。
接下来总结一下回归的方法:
我们可以先把找重要的特性,然后数据可视化,观察数据的分布特点然后决定预测方式。
可以选择简单的线性回归,如果要挖掘数据的潜在价值我们用LWLR并设置合适的k。
当特征数大于样本数时,我们用岭回归的方式,多次选择不同的设置值并交叉验证出一个最佳的w作为拟合权值。
这一章学的不好,明天进行cart的学习。