uva 375 Inscribed Circles and Isosceles Triangles(相似三角形)
| Inscribed Circles and Isosceles Triangles |
Given two real numbers
- B
- the width of the base of an isosceles triangle in inches
- H
- the altitude of the same isosceles triangle in inches
Compute to six significant decimal places
- C
- the sum of the circumferences of a series of inscribed circles stacked one on top of another from the base to the peak; such that the lowest inscribed circle is tangent to the base and the two sides and the next higher inscribed circle is tangent to the lowest inscribed circle and the two sides, etc. In order to keep the time required to compute the result within reasonable bounds, you may limit the radius of the smallest inscribed circle in the stack to a single precision floating point value of 0.000001.
For those whose geometry and trigonometry are a bit rusty, the center of an inscribed circle is at the point of intersection of the three angular bisectors.
Input
The input begins with a single positive integer on a line by itself indicating the number of the cases following, each of them as described below. This line is followed by a blank line, and there is also a blank line between two consecutive inputs.
The input will be a single line of text containing two positive single precision real numbers (B H) separated by spaces.
Output
For each test case, the output must follow the description below. The outputs of two consecutive cases will be separated by a blank line.
The output should be a single real number with twelve significant digits, six of which follow the decimal point. The decimal point must be printed in column 7.
Sample Input
1 0.263451 0.263451
Sample Output
0.827648
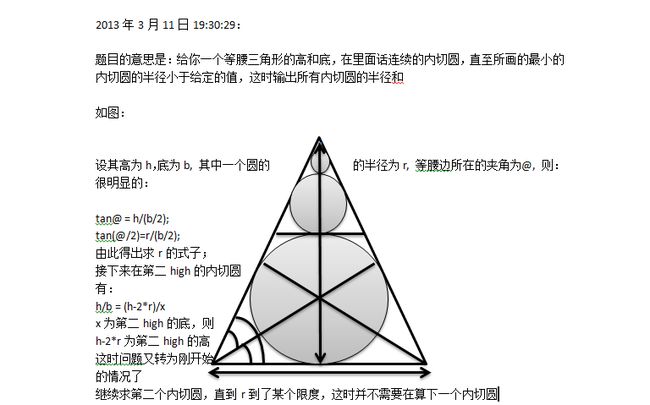
题目大意:图片从别人哪里拷贝的,觉得解释的很清楚。
解题思路:最早用
leap = sqrt(b * b + h * h); r = (b * h * 0.5) / (leap +b);
的方法,但是涉及到除法,精度有误差,所以WA了。
#include<stdio.h>
#include<iostream>
#include<math.h>
using namespace std;
int main(){
double b, h;
int t;
const double pi = 4 * atan(1.0);
cin >> t;
while (t--){
cin >> b >> h;
double sum = 0;
while (1){
double leap = atan(h /(b / 2));
double r = tan(leap / 2) * b / 2;
if (r < 0.000001)
break;
sum += 2 * pi * r;
b = b * (h - 2 * r) / h;
h = h - 2 * r;
}
printf("%13.6lf\n", sum);
if (t)
cout << endl;
}
return 0;}