How to choose Approximate Nearest Neighbors Searching Algorithms？

      CV人可能比较了解Approximate Nearest Neighbors Searching Algorithms(ANN)吧，因为打得交道实在是太多了。不管是Image matching/Image retrieval/Image stitching/Image recognition，最后一步总是NN searching。这一周被各种NN searching折磨着，总算有些心得体会，希望大家一起来讨论。

 

     1.实例说明ANN的魅力

             

                                                                 图1

 

      

                                                               图2                                                

                                                                            

 

      图1是利用pLSA进行图像分类时利用Vocabulary Tree生成Document Vector的过程，利用到了ANN；

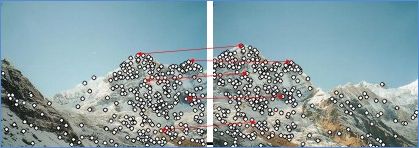
      图2是图像拼接过程中对应点匹配的问题，利用到了ANN。

 

     2.Search Algorithms

          

                                                                                                      图3

      由图3，Linear search就是线性搜索，即把query point与dataset里面的所有值进行比较，直到选出比较满意的对应点停止。这种方法只能处理规模比较小的数据库，要不然时间复杂度会很高。同时，NN的方法主要包含三种：K-means tree、KD-tree和LSH(locally senstive hashing)，在这里我们主要讨论前两种方法。

 

     3.KD-tree

     KD-tree是K dimensional tree的缩写，K表明tree里面所有的节点都是K维的。

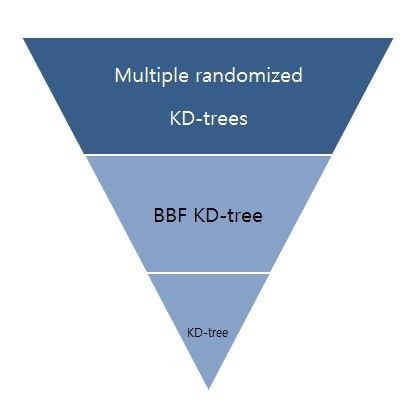
     KD-tree的发展史如图4所示：KD-tree -> BBF KD-tree -> Multiple randomized KD-tree

                                   

                                                                        图4

      

           3.1 KD-tree

           KD-tree是一种二叉树，所以它的分支只有两个。图5是它的形成过程。

          

                                                                                                        图5

             具体的形成过程，我就不写了，请参考博客   http://blog.csdn.net/v_july_v/article/details/8203674，这篇博客可以说是我看到写的最好的了。

            3.2 BBF KD-tree

            这才是我要讲的重点，我看了很多博客，感觉写的都不是很明白，所以我希望自己可能写的比较清楚（有错误的话，欢迎拍砖，但要轻拍） 

            

                                                                                                  图6

            图6左边是最原始的KD-tree方法。假设我们要搜素（2,4.5）点   我们说的路径是PATH 1，即找到了(4,7)点（1st candidate），然后根据KD-tree的算法原理，我们需要把backtrack，首先到(5,4)点，发现查找点与(5,4)的距离反而小，然后以查找点为圆心，query point与(5,4)的距离为半径画圆，我们发现在这个圆的范围内存在(2,3)点，所以(2,3)为2nd candidate，然后回溯到(5,4)点，最后回溯到根节点。

           而BBF KD-tree与KD-tree最大的区别有两个：

           第一：BBF建立了优先队列（priority queue），回溯的时候只考虑优先队列；

           第二：BBF提出停止查找的两个条件——优先队列为空或者查找次数（# node search）超过我们设定的阈值（predetermined number）。

         

          下面就要讨论本文最有意思的部分：如何建立优先队列？？？

 

          首先说明的是，BBF中优先队列是在查找过程中建立的，与查找同时进行。如图6右下方所示。

          第一步：把根节点放到优先队列中，此时优先队列有(7,2)一项；

          第二步：在查找过程时，取出(7,2)，因为(7,2)是暂时放入优先队列的根节点。

          第三步：走到了(5,4)点，与此同时把同一个父节点没有被查询的点放入优先队列，即(9,6)被放入优先队列【此时(9,6)距其父节点的距离为2，我们只考虑X方向上的】。此时我们只知道(7,2)与查询点的距离，此时离查询点最近的是(7,2)；

          第四步：走到了(4,7)点，同时把(2,3)放入优先队列【(2,3)与其父节点的距离为1，我们只考虑Y方向上的】。通过比较(5,4)与(7,2)和查询点的距离，我们发现此时离查询点最近的是(5,4)；

          第五步：开始回溯，把优先级别高【与父节点的距离越近的，优先级别越高】的(2,3)从优先队列中提出。通过比较(2,3)与(5,4)和查询点的距离，我们发现此时离查询点最近的是(2,3)；

          第六步：把优先队列中已经进行比较的(2,3)点拿出，计算(9,6)与查询点的距离。通过比较(9,6)与(2,3)和查询点的距离，我们发现此时离查询点最近的是(2,3)；

          第七步：取出(9,6),此时优先队列为空，停止查找。

                   

                                                                                                      图7                                                

         

 

        从图7我们可以看出，在数据维数小于23的空间，Kd-tree的检索速度更快；但实际中的数据往往都是高维的，BBF使得KD-tree可以用在高维空间，而且从时间复杂度看比KD-tree更有效。

        上图来自于Shape Indexing Using Approximate Nearest-Neighbor Search in High-Dimensional Spaces --Jeffrey S.Beis andDavid G. Lowe

 

        3.3 Multiple randomized KD-tree

        

                                                                               图8

          

       在这我简单介绍一下multiple randomized KD-tree,想了解详情的请参考论文：OptimizedKD-trees for fast image descriptor matching--Silpa Anan & Hartley

 

       “Multiple”说明树的个数不止一个。同一个dataset形成独立的不同结构trees；

       “randomized”是相对于KD-tree选择split dimension的方法而言的。KD-tree中通过选择对应于最大variance的那个维作为分割维数；在这，因为高维空间的维数实在太大，要是一一计算每一位相对应的方差，实在是个力气活。科学家都是懒人，所以他们从K多维中随机选取了D维（本文中D=5），通过计算这D维中中的方差，选择最大方差对应的维作为分割维数。

                                               

                        

         从上图中我们发现不能建太多的树，大概在20个树左右效果最好，多于这个数目，可能效果反而变差，而且建树也需要大量时间。

 

         4.K-means tree

         4.1 K-means tree

          因为这个比较常见，大家可以参考这篇博文： http://www.csdn.net/article/2012-07-03/2807073-k-means                                             

                          在这里面有DEMO  http://home.deib.polimi.it/matteucc/Clustering/tutorial_html/AppletKM.html

         强调一点——这的K是聚类数，也可以认为是分枝数。

 

         4.2 Hierarchical K-means tree (vocabulary tree)                                     

   

                                                

                    有兴趣的同学可以参考这篇论文： ScalableRecognition with a Vocabulary Tree--DavidNister,HenrikStewenius

          感慨一下：大牛就是大牛，文思如泉涌。

          下面我们来看一下，影响hierarchical k-means tree的因素有两个：分枝树和迭代次数。

 

                      

         我们从图中可以看出，当迭代此时在7的时候，它的效果已经非常好了。随着迭代次数的增加，效果提升一点，但却要牺牲很多的时间。所以，我们一定要控制迭代的次数。

 

 

 

        5 如何选择ANN算法

        终于到这了，感觉写博客是力气活啊，不适合小女生。话说工科女是不是都是外表柔弱内心强大啊~

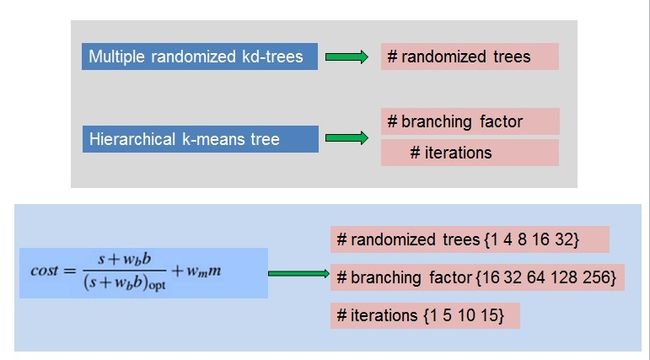
        影响算法performance的因素很多，例如：datas的结构和特点。其中每个算法还有很多的parameters，从另一个角度看，这就相当于在参数空间求极值的问题。

               

        这篇文章Fast Approximate Nearest Neighbors with Automatic Algorithm Configuration最大的贡献之一就是建立了这么一个cost的目标方程。而我们的目标就是在参数空间内最小化cost方程。

       简单介绍一下cost方程：

       s：searching time，搜索树的时间；

       b：building time，建树的时间；

       m：memory，内存；

       w表示对应的权重。

       可见cost分为两部分，time overhead和memory overhead。

        两步走：

        第一步，根据大量实验经验，对参数空间进行取样；

        第二步，利用单纯形法，从取样空间选出最优的那个参数值。

 

 

       6.结果

                     

                                                                                                  结果1

 

         我们分析一下：红框表示在建树时间和内存占有的权重最大的时候，我们要采用single KD-tree方法，因为它最容易建立而且在内存上比较有效率；绿框表示在建树时间和内存占有的权重最小的时候，我们要采用k-means方法。纵向比较，当要达到较高的精度时，我们要多分枝，但是迭代次数要保证在一定的范围内。

 

                              

                                                                                                     结果2

          从结果图2(a),我们可以发现k-means和KD-tree比现有的LSH，ANN的效果好（这里的ANN是指k-means/kd-tree的原始版本）；

                           (b),我们发现在一定的精度下，我们的算法在速度上可以是线性搜索的3个数量级，也就是时间是线性搜索的千分之一这样，但是要想达到几乎完美的搜索，时间上也要消耗很多；

                           (c),这个dataset比较特别，有一个几乎完全能matching点的数据集，采自于进行image stitching的overlapping 区域，有一个是几乎不能匹配的数据集，这个比较好解决，不多说。

                               我们发现，ran.KD-tree的效果比kmeans好，也就是说如果我们的query image和women的dataset有一种联系，例如transformed的关系，我们采用ran.KD-tree;

                           (d),在数据集的本征维数小于实际维数的情况下，ran.KD-tree的效果比较好。

 

 

 

 

         7.FLANN

         这个我还没用，过两天贴感受。现在去吃饭，饿死啦啦啦啦啦~~