Machine Learning week 1 Octave Tutorial
1 Basic operation
加减乘除指数
3 - 2
5 x 8
1/2
2^6
等于不等于,或且非运算,结果是1 或者 0
1==2
true == false
true != false
true | false
true & false
~true
小数的长短格式
format short : 14位小数
format long: 4位小数
a = [1:0.2:2] :以0.2为步长,1到2的一维数组
Rand(3) : 1x3 随机数字数组
Randn(2,3): 2x3 随机正态分布数组
hist() :直方图
ones(3) :1x3全一数组
zeros(3,4): 3x4 全零数组
eye(4): 4x4单位矩阵
help eye:获取eye函数的帮助文档
2 Moving Data Around
A=[1,2,3;4,5,6] :生成一个2x3的矩阵
size(A) :获得[2,3],分别是A的行数和列数
size(A,1): 结果是2,返回A的行数
length(A): 结果是A的较大的维度的数值,这里结果为3
pwd 打印当前路径
cd ‘C:\USER\XXX\’ 可以修改当前路径
ls 列出当前路径下的文件列表
load('featureX.dat') 可以用来加载文件中的数据(格式规范的数据,行列)
who 可以列出当前工作区有效的变量
whos可以列出更为详细的信息
v = featureX(1:10) v赋值为featureX的前10个元素组成的数组
save hello.mat v 可以把v的数值存储到hello.mat中,这里连变量名字也一起存储了,二进制格式
clear 可以清掉工作台上所有的变量
load hello.mat 可以把变量v恢复回来
save hello.txt v -ascii %以文本方式存储
A(2,3) 可以得到第二行第三列的A的元素
A(2,:) 可以获得第二行的所有元素
A([1 3], :) 可以获得第一行和第三行的所有数据
A(:,2) = [1;2;3] 可以修改A的元素内容
A = [A, [1;2;3]] 相当于在A的右边增加一列
A(:) 获得把所有列,排列成为一列的输出
C = [A B] 把A,B并排做成一个矩阵
C = [A;B] 把B补充为A新的行
3 Computing on Data
A = [1,2;3,4]
B = [1,2;3,4]
C = A.*B 点乘表示对应位置的数字相乘
C = A*B 矩阵相乘
A = B.^2 每个元素平方组成新的矩阵
B^2 就变成两个B相乘了
C = 1./ A 这样可以得到每个元素的倒数
log(A) 这个也是针对每个元素的操作
exp(A) 返回自然常熟e的A指数矩阵
abs(A) 每个元素的绝对值矩阵
-1 * A 给A的每个元素乘以一个倍数
A + ones(length(A), size(A,2)), 可以给A的每个元素增加一个1
A + 1 每个元素增加1
A' 表示A的转置,这里的符号是左单引号
A = [1,2,3,4,5]
max(A) :这里只返回最大值
[val,ind] = max(A) :这里的结果val是最大值,ind是最大值的index
A<3 这里的比较操作也是每个元素单独进行的
find(A<3) :结果会返回A中小于3的所有元素的index
A = magic(3), 会生成一个3x3的矩阵,每一行每一列加的结果相等
[r,c] = find(A < 3) : r是所有满足结果的行号,c是响应的列好
A = [1 2 3 4 5]
sum(A) 返回A的所有元素的和
prod(A) 返回素有A的元素的积
floor(A), ceil(A) 返回A中所有元素的round之后的值
max(A,[],1) 返回A的没列的最大值
max(A,[],2) 返回A的每行的最大值
A = [1 2; 2 1]
max(A) : 结果是2 2,是没列的最大值
max(max(A)) 可以求得全局最大值
max(A(:)) 也可以可以求得全局最大值
A = [1 3; 2 5]
sum(A) 返回每列的和
sum(A, 1) 同上
sum(A, 2) 每行和
那么我们怎么计算A的对角线的和呢
B = A.* eye(2)
sum(sum(B)) 就是A的对角线的元素的和
flipud(A) 可以把A的元素翻转,指的是每列的内容都进行翻转
pinv(A) 计算A的逆
3 Plotting Data
x = [0:0.01:0.98]
y = sin(2*pi*4*x)
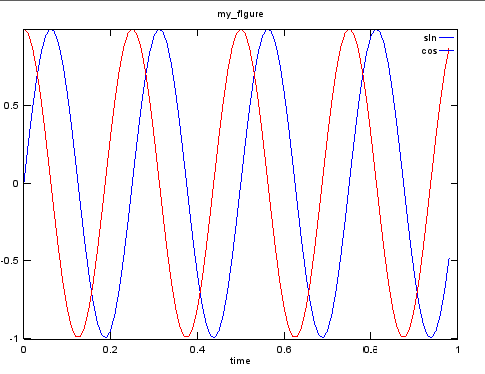
plot(x,y) 可以画出正弦曲线来
hold on 可以继续在之前的图上继续画新的图像
y2 = cos(2*pi*4*x)
plot(x,y2,'r') 可以在上一个正弦曲线的基础上画出一条红色的余弦曲线
xlabel(‘time’)
ylabel('value') 为横纵坐标轴加上lable
legend('sin', 'cos') 标注每个曲线的名称
title('my figure')
print -dpng 'my.png' 这之前可以修改cd路径
也可以在不同的图上面画不同的曲线
figure(1); plot(x,y);
figure(2); plot(x,y2) 这样就会有两个图,每个上面有一个曲线
subplot(1,2,1); plot(x,y);
subplot(1,2,2); plot(x,y2); 这样两个曲线在同一个frame里面,这个frame分成了1x2的部分,y=f(x)在其中的第一个部分,另一个在第二部分
axis([0.5 1 -1 1]) 这样可以设置图像横纵坐标的取值范围,分别为[0.5 1] 和[-1 1]
clf; clear figure
A=magic(5)
imagesc(A)
imagesc(A), colorbar, colormap gray
4 控制语句
for loop
v = zeros(10)
for i=1:10,
v(i) = 2^i;
end;
indices = 1:10
for i=indices,
disp(i);
end;
while
i = 0;
while i<5,
v(i)=100;
i = i+1;
end;
i = 0;
while i<10,
v(i)=100;
i = i+1;
if i == 6,
break;
end;
end;
if i==1,
disp(i);
elseif i==2,
disp(i);
else
disp(i);
end;
Function
function y = sqareThisNum(x)
y = x^2;
就可以调用函数sqareThis Num()了,他有一个input X, 一个output Y
function [y1,y2] = my_func(x)
y1 = x^2;
y2 = x^3;
[a,b] = my_func(5); 可以这样调用函数
addpath('C:\XXX\XXAAA\AAA'); 可以把路径加入octave的搜索路径中
5 Vectorrization
Octave的index是从1开始的