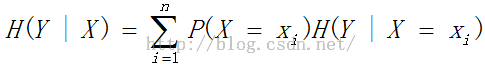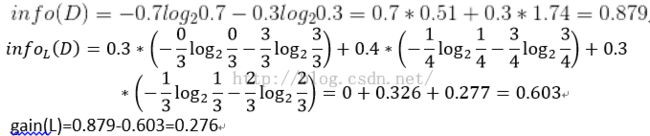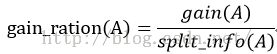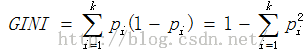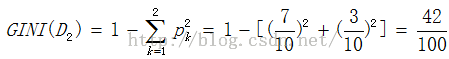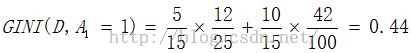机器学习系列05——决策树（Decision tree）

决策树（Decision tree）

1、引入

       通俗来说，决策树分类的思想类似于找对象。现想象一个女孩的母亲要给这个女孩介绍男朋友，于是有了下面的对话：

        这个女孩的决策过程就是典型的分类树决策。相当于通过年龄、长相、收入和是否公务员对将男人分为两个类别：见和不见。假设这个女孩对男人的要求是：30岁以下、长相中等以上并且是高收入者或中等以上收入的公务员，那么这个可以用下图表示女孩的决策逻辑。

       上图完整表达了这个女孩决定是否见一个约会对象的策略，其中绿色节点表示判断条件，橙色节点表示决策结果，箭头表示在一个判断条件在不同情况下的决策路径，图中红色箭头表示了上面例子中女孩的决策过程。

2、定义

        决策树（decision tree）是一个树结构（可以是二叉树或非二叉树）。其每个非叶节点表示一个特征属性上的测试，每个分支代表这个特征属性在某个值域上的输出，而每个叶节点存放一个类别。使用决策树进行决策的过程就是从根节点开始，测试待分类项中相应的特征属性，并按照其值选择输出分支，直到到达叶子节点，将叶子节点存放的类别作为决策结果。

3、决策树的构造

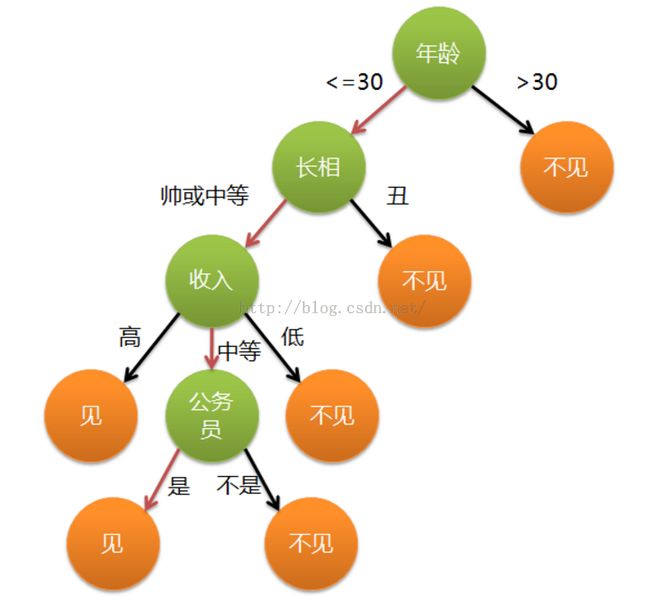
       不同于贝叶斯算法，决策树的构造过程不依赖领域知识，它使用属性选择度量来选择将元组最好地划分成不同的类的属性。所谓决策树的构造就是进行属性选择度量确定各个特征属性之间的拓扑结构。

       构造决策树的关键步骤是分裂属性。所谓分裂属性就是在某个节点处按照某一特征属性的不同划分构造不同的分支，其目标是让各个分裂子集尽可能地“纯”。尽可能“纯”就是尽量让一个分裂子集中待分类项属于同一类别。分裂属性分为三种不同的情况：

     1、属性是离散值且不要求生成二叉决策树。此时用属性的每一个划分作为一个分支。

     2、属性是离散值且要求生成二叉决策树。此时使用属性划分的一个子集进行测试，按照“属于此子集”和“不属于此子集”分成两个分支。

     3、属性是连续值。此时确定一个值作为分裂点split_point，按照>split_point和<=split_point生成两个分支。

       构造决策树的关键性内容是进行属性选择度量，属性选择度量是一种选择分裂准则，是将给定的类标记的训练集合的数据划分D“最好”地分成个体类的启发式方法，它决定了拓扑结构及分裂点split_point的选择。

       属性选择度量算法有很多，一般使用 自顶向下递归分治法，并采用 不回溯的贪心策略。这里介绍ID3和C4.5两种常用算法。

4、ID3算法

        ID3算法主要针对特征选择问题，使用信息增益准则选择特征属性。

4.1、信息论——熵

        如果一件事有n种可能的结果，每种结果的概率为 那么熵为：

        熵越大，随机变量的不确定性（出去活动或取消活动）就越大。

4.2、条件熵

        条件熵H(Y|X)表示在已知随机变量X的条件下随机变量Y的不确定性。例如，知道天气的情况下，决定是否进行户外活动的不确定性。

         熵与条件熵中概率由训练数据估计得到时，所对应的熵和条件熵称为经验熵和经验条件熵。若概率为0，令0log0=0。

4.3、信息增益

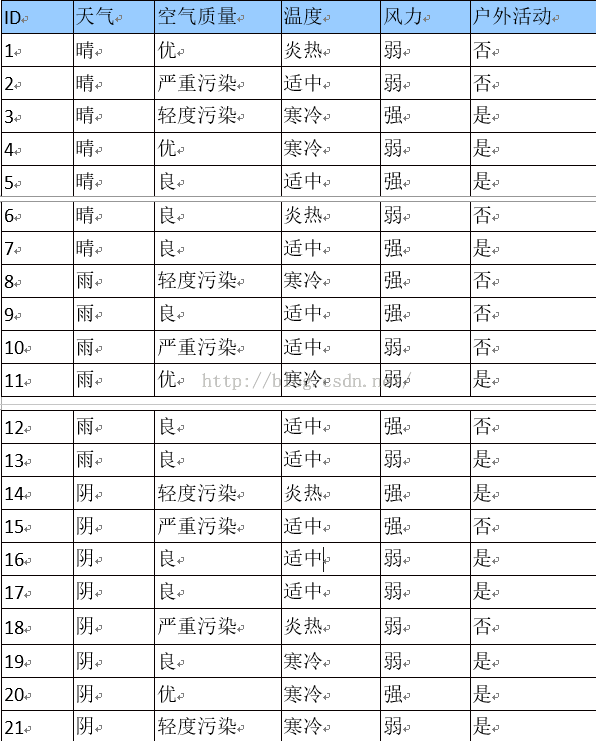
       信息增益表示得知特征X(天气)的信息使得类Y(进行户外活动或取消活动)的信息的不确定性减少程度。

       特征A对训练数据集D的信息增益g(D,A)，定义为集合D的经验熵H(D)与特征A给定条件下的经验条件熵H(D|A)之差，即

       熵H(Y)与条件熵H(Y|X)之差称为互信息，即g(D,A)

       信息增益大表明信息多，信息增多，则不确定性就越小。

        

        数据集D，计算每个特征的信息增益，并比较他们的大小，选择信息增益最大的特征。

4.4、ID3思想

ID3算法的核心是在决策树各个子结点上应用信息增益准则选择特征，递归的构建决策树。
具体方法是:从根结点开始，对结点计算所有可能的特征的信息增益，选择信息增益最大的特征作为结点的特征，由该特征的不同取值建立子结点；再对子结点递归调用以上方法，构建决策树。直到所有特征的信息增益均很小或没有特征可以选择为止。

4.5、ID3算法实例

        ID3算法就是在每次需要分裂时，计算每个属性的增益率，然后选择增益率最大的属性进行分裂。下面我们继续用SNS社区中不真实账号检测的例子说明如何使用ID3算法构造决策树。为了简单起见，我们假设训练集合包含10个元素：

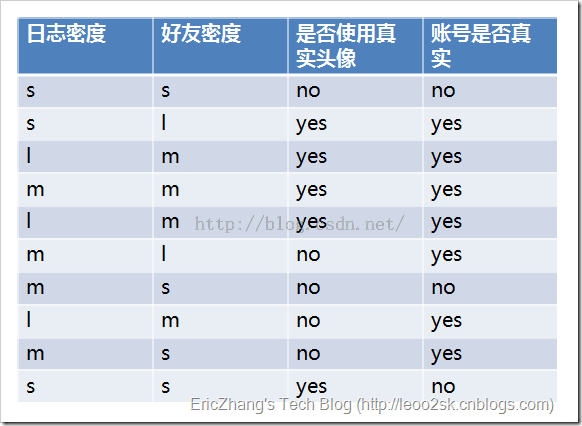
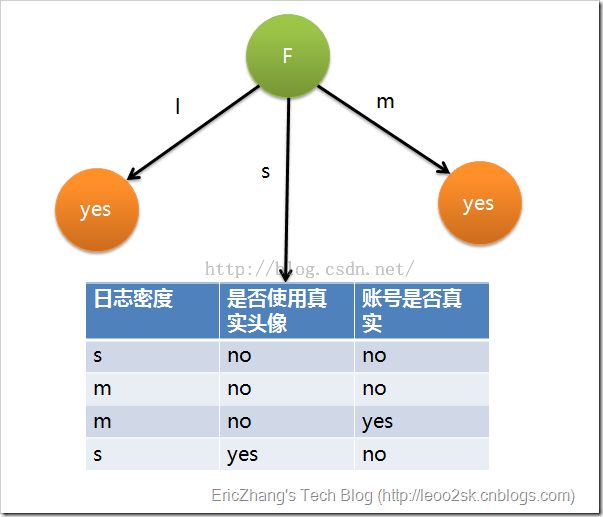
       其中s、m和l分别表示小、中和大。

       设L、F、H和R表示日志密度、好友密度、是否使用真实头像和账号是否真实，下面计算各属性的信息增益。

        因此日志密度的信息增益是0.276.

        用同样方法得到H和F的信息增益分别为0.033和0.553。

        因为F具有最大的信息增益，所以第一次分裂选择F为分裂属性，分裂后的结果如下图表示：

     在上图的基础上，再递归使用这个方法计算子节点的分裂属性，最终就可以得到整个决策树。

     上面为了简便，将特征属性离散化了，其实日志密度和好友密度都是连续的属性。对于特征属性为连续值，可以如此使用ID3算法：

      先将D中元素按照特征属性排序，则每两个相邻元素的中间点可以看做潜在分裂点，从第一个潜在分裂点开始，分裂D并计算两个集合的期望信息，具有最小期望信息的点称为这个属性的最佳分裂点，其信息期望作为此属性的信息期望。

5、C4.5算法

        ID3算法存在一个问题，就是偏向于多值属性，例如，如果存在唯一标识属性ID，则ID3会选择它作为分裂属性，这样虽然使得划分充分纯净，但这种划分对分类几乎毫无用处。ID3的后继算法C4.5使用增益率（gain ratio）的信息增益扩充，试图克服这个偏倚。

        C4.5算法首先定义了“分裂信息”，其定义可以表示成：

        其中各符号意义和ID3算法相同，然后增益率定义为：

         C4.5选择具有最大增益率的属性作为分裂属性，其具体应用于ID3类似。

6、CART算法

       分类回归树(CART,Classification And Regression Tree)其核心思想与ID3和C4.5相同，主要的不同处在于CART在每一个节点上都采用二分法，即每个节点都只能有两个子节点，最后构成的是二叉树。

       CART树由两步组成：

           (1)决策树的生成：基于训练数据集生成决策树；

           (2)决策树的剪枝：对生成的树进行剪枝并选择最优子树。

6.1、基尼指数

       CART分类树通常采用基尼指数(GINI)选择最优特征，同时决定该特征的最优二值切分点。总体内包含的类别越杂乱，GINI指数就越大（跟熵的概念很相似）。

       分类问题中，假设有k个类，样本点属于第i类的概率为pi，则基尼指数定义为

6.2、CART生成树

       分别以A1，A2，A3，A4表示年龄、有工作、有自己的房子和信贷情况4个特征。以1,2,3表示年龄的值为青年、中年、老年，以1,2表示有工作和有自己的房子的值为是和否，以1,2,3表示信贷情况的值为非常好、好和一般。

      将年龄划分为青年，非青年的样本数。

       总的样本集合D根据特征A1（年龄），将数据集D划分为D1(青年)，D2(非青年)，那么在特征为年龄的条件下，数据集D的基尼指数：

（1）年龄为青年的样本

（2）年龄为非青年的样本

（3）将年龄分为青年与非青年的基尼指数：

将年龄分为中年与非中年的基尼指数：

将年龄分为老年与非老年的基尼指数：

求特征A2和A3的基尼指数如下，

只有一个切分点，所以它们就是最优切分点。

求A4的基尼指数：

在A1，A2，A3, A4几个特征中，找最小的基尼指数。

选A3=1作为最优的切分点，即根结点。生成两个子结点，一个为叶结点，另外一个按照类似于ID3的过程，递归再选最优切分点，直到划分完成。

6.3、CART剪枝

      当CART树划分得太细时，会对噪声数据产生过拟合作用。因此我们要通过剪枝来解决。剪枝又分为前剪枝和后剪枝。

       前剪枝是指在构造树的过程中就知道哪些节点可以剪掉，于是干脆不对这些节点进行分裂。

       后剪枝是指构造出完整的决策树之后再来考查哪些子树可以剪掉。

       CART剪枝算法从“完全生长”的决策树的底端剪去一些子树，使决策树变小(模型变简单)，从而能够对未知数据有更准确的预测。

       CART树中的每一个非叶子节点的表面误差率增益值α(误差增加的速率，越小越好)

       是子树中包含的叶子节点个数。

        是节点t的误差代价，如果该节点被剪枝：

        

         r(t)是节点t的误差率；

         p(t)是节点t上的数据占所有数据的比例；

        是子树T_t的误差代价，如果该节点不被剪枝，它等于子树T_t上所有叶子节点的误差代价之和。

6.3.1、代价误差

有个非叶子节点t4如图所示：

已知所有的数据总共有60条，则节点t4的节点误差代价为：

注意:叶子节点的类定义为覆盖的样本占多数的类，即分正确的为多数，分错的为少数。

子树误差代价为：

以t4为根节点的子树上叶子节点有3个，最终：

找到α值最小的非叶子节点，令其左右孩子为空，即该节点成为叶子节点，即剪枝。