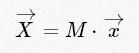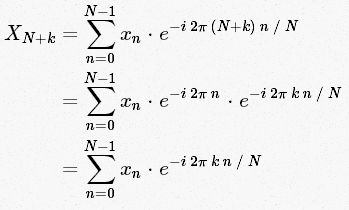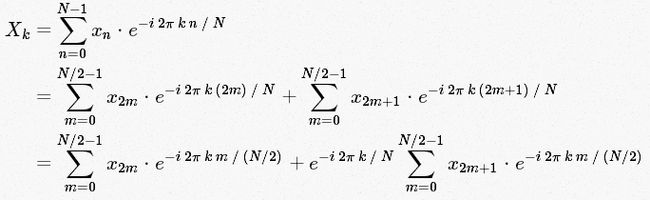理解快速傅里叶变换(FFT)算法
快速傅里叶变换(Fast Fourier Transform)是信号处理与数据分析领域里最重要的算法之一。没有正规计算机科学课程背景的我,使用这个算法多年,但这周我却突然想起自己从没思考过为什么FFT能如此快速地计算离散傅里叶变换。我打开一本老旧的算法书,欣赏了JW Cooley 和 John Tukey 在1965年的文章中,以看似简单的计算技巧来讲解这个东西。
本文的目标是,深入Cooley-Tukey FFT 算法,解释作为其根源的“对称性”,并以一些直观的python代码将其理论转变为实际。我希望这次研究能使数据科学家(例如我),对这个算法的背景原理有更全面的认识。
FFT(快速傅里叶变换)本身就是离散傅里叶变换(Discrete Fourier Transform)的快速算法,使算法复杂度由原本的O(N^2) 变为 O(NlogN),离散傅里叶变换DFT,如同更为人熟悉的连续傅里叶变换,有如下的正、逆定义形式:
xn 到 Xk 的转化就是空域到频域的转换,这个转换有助于研究信号的功率谱,和使某些问题的计算更有效率。事实上,你还可以查看一下我们即将推出的天文学和统计学的图书的第十章(这里有一些图示和python代码)。作为一个例子,你可以查看下我的文章《用python求解薛定谔方程》,是如何利用FFT将原本复杂的微分方程简化。
正因为FFT在那么多领域里如此有用,python提供了很多标准工具和封装来计算它。NumPy 和 SciPy 都有经过充分测试的封装好的FFT库,分别位于子模块 numpy.fft 和 scipy.fftpack 。我所知的最快的FFT是在 FFTW包中 ,而你也可以在python的pyFFTW 包中使用它。
虽然说了这么远,但还是暂时先将这些库放一边,考虑一下怎样使用原始的python从头开始计算FFT。
计算离散傅里叶变换
简单起见,我们只关心正变换,因为逆变换也只是以很相似的方式就能做到。看一下上面的DFT表达式,它只是一个直观的线性运算:向量x的矩阵乘法,
矩阵M可以表示为
这么想的话,我们可以简单地利用矩阵乘法计算DFT:
|
1
2
3
4
5
6
7
8
9
|
import
numpy as np
def
DFT_slow(x):
"""Compute the discrete Fourier Transform of the 1D array x"""
x
=
np.asarray(x, dtype
=
float
)
N
=
x.shape[
0
]
n
=
np.arange(N)
k
=
n.reshape((N,
1
))
M
=
np.exp(
-
2j
*
np.pi
*
k
*
n
/
N)
return
np.dot(M, x)
|
对比numpy的内置FFT函数,我们来对结果进行仔细检查,
|
1
2
|
x
=
np.random.random(
1024
)
np.allclose(DFT_slow(x), np.fft.fft(x))
|
输出:
True
现在为了验证我们的算法有多慢,对比下两者的执行时间
|
1
2
|
%
timeit DFT_slow(x)
%
timeit np.fft.fft(x)
|
输出:
10 loops, best of 3: 75.4 ms per loop 10000 loops, best of 3: 25.5 µs per loop
使用这种简化的实现方法,正如所料,我们慢了一千多倍。但问题不是这么简单。对于长度为N的输入矢量,FFT是O(N logN)级的,而我们的慢算法是O(N^2)级的。这就意味着,FFT用50毫秒能干完的活,对于我们的慢算法来说,要差不多20小时! 那么FFT是怎么提速完事的呢?答案就在于他利用了对称性。
离散傅里叶变换中的对称性
算法设计者所掌握的最重要手段之一,就是利用问题的对称性。如果你能清晰地展示问题的某一部分与另一部分相关,那么你就只需计算子结果一次,从而节省了计算成本。
Cooley 和 Tukey 正是使用这种方法导出FFT。 首先我们来看下的值。根据上面的表达式,推出:
对于所有的整数n,exp[2π i n]=1。
最后一行展示了DFT很好的对称性:
简单地拓展一下:
![]()
同理对于所有整数 i 。正如下面即将看到的,这个对称性能被利用于更快地计算DFT。
DFT 到 FFT:
利用对称性 Cooley 和 Tukey 证明了,DFT的计算可以分为两部分。从DFT的定义得:
我们将单个DFT分成了看起来相似两个更小的DFT。一个奇,一个偶。目前为止,我们还没有节省计算开销,每一部分都包含(N/2)∗N的计算量,总的来说,就是N^2 。
技巧就是对每一部分利用对称性。因为 k 的范围是 0≤k<N , 而 n 的范围是 0≤n<M≡N/2 , 从上面的对称性特点来看,我们只需对每个子问题作一半的计算量。O(N^2) 变成了 O(M^2) 。
但我们不是到这步就停下来,只要我们的小傅里叶变换是偶倍数,就可以再作分治,直到分解出来的子问题小到无法通过分治提高效率,接近极限时,这个递归是 O(n logn) 级的。
这个递归算法能在python里快速实现,当子问题被分解到合适大小时,再用回原本那种“慢方法”。
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
def
FFT(x):
"""A recursive implementation of the 1D Cooley-Tukey FFT"""
x
=
np.asarray(x, dtype
=
float
)
N
=
x.shape[
0
]
if
N
%
2
>
0
:
raise
ValueError(
"size of x must be a power of 2"
)
elif
N <
=
32
:
# this cutoff should be optimized
return
DFT_slow(x)
else
:
X_even
=
FFT(x[::
2
])
X_odd
=
FFT(x[
1
::
2
])
factor
=
np.exp(
-
2j
*
np.pi
*
np.arange(N)
/
N)
return
np.concatenate([X_even
+
factor[:N
/
2
]
*
X_odd,
X_even
+
factor[N
/
2
:]
*
X_odd])
|
现在我们做个快速的检查,看结果是否正确:
|
1
2
|
x
=
np.random.random(
1024
)
np.allclose(FFT(x), np.fft.fft(x))
|
True
然后与“慢方法”的运行时间对比下:
|
1
2
3
|
%
timeit DFT_slow(x)
%
timeit FFT(x)
%
timeit np.fft.fft(x)
|
10 loops, best of 3: 77.6 ms per loop 100 loops, best of 3: 4.07 ms per loop 10000 loops, best of 3: 24.7 µs per loop
现在的算法比之前的快了一个数量级。而且,我们的递归算法渐近于 O(n logn) 。我们实现了FFT 。
需要注意的是,我们还没做到numpy的内置FFT算法,这是意料之中的。numpy 的 fft 背后的FFTPACK算法 是以 Fortran 实现的,经过了多年的调优。此外,我们的NumPy的解决方案,同时涉及的Python堆栈递归和许多临时数组的分配,这显著地增加了计算时间。
还想加快速度的话,一个好的方法是使用Python/ NumPy的工作时,尽可能将重复计算向量化。我们是可以做到的,在计算过程中消除递归,使我们的python FFT更有效率。
向量化的NumPy
注意上面的递归FFT实现,在最底层的递归,我们做了N/32次的矩阵向量乘积。我们的算法会得益于将这些矩阵向量乘积化为一次性计算的矩阵-矩阵乘积。在每一层的递归,重复的计算也可以被向量化。因为NumPy很擅长这类操作,我们可以利用这一点来实现向量化的FFT。
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
|
def
FFT_vectorized(x):
"""A vectorized, non-recursive version of the Cooley-Tukey FFT"""
x
=
np.asarray(x, dtype
=
float
)
N
=
x.shape[
0
]
if
np.log2(N)
%
1
>
0
:
raise
ValueError(
"size of x must be a power of 2"
)
# N_min here is equivalent to the stopping condition above,
# and should be a power of 2
N_min
=
min
(N,
32
)
# Perform an O[N^2] DFT on all length-N_min sub-problems at once
n
=
np.arange(N_min)
k
=
n[:,
None
]
M
=
np.exp(
-
2j
*
np.pi
*
n
*
k
/
N_min)
X
=
np.dot(M, x.reshape((N_min,
-
1
)))
# build-up each level of the recursive calculation all at once
while
X.shape[
0
] < N:
X_even
=
X[:, :X.shape[
1
]
/
2
]
X_odd
=
X[:, X.shape[
1
]
/
2
:]
factor
=
np.exp(
-
1j
*
np.pi
*
np.arange(X.shape[
0
])
/
X.shape[
0
])[:,
None
]
X
=
np.vstack([X_even
+
factor
*
X_odd,
X_even
-
factor
*
X_odd])
return
X.ravel()
|
|
1
2
|
x
=
np.random.random(
1024
)
np.allclose(FFT_vectorized(x), np.fft.fft(x))
|
True
因为我们的算法效率更大幅地提升了,所以来做个更大的测试(不包括DFT_slow)
|
1
2
3
4
|
x
=
np.random.random(
1024
*
16
)
%
timeit FFT(x)
%
timeit FFT_vectorized(x)
%
timeit np.fft.fft(x)
|
10 loops, best of 3: 72.8 ms per loop 100 loops, best of 3: 4.11 ms per loop 1000 loops, best of 3: 505 µs per loop
我们的实现又提升了一个级别。这里我们是以 FFTPACK中大约10以内的因数基准,用了仅仅几十行 Python + NumPy代码。虽然没有相应的计算来证明, Python版本是远优于 FFTPACK源,这个你可以从这里浏览到。
那么 FFTPACK是怎么获得这个最后一点的加速的呢?也许它只是一个详细的记录簿, FFTPACK花了大量时间来保证任何的子计算能够被复用。我们这里的numpy版本涉及到额外的内存的分配和复制,对于如Fortran的一些低级语言就能够很容易的控制和最小化内存的使用。并且Cooley-Tukey算法还能够使其分成超过两部分(正如我们这里用到的Cooley-Tukey FFT基2算法),而且,其它更为先进的FFT算法或许也可以能够得到应用,包括基于卷积的从根本上不同的方法(例如Bluestein的算法和Rader的算法)。结合以上的思路延伸和方法,就可使阵列大小即使不满足2的幂,FFT也能快速执行。
我希望他们提供大量的基于FFT数据分析是怎样进行的背景,尽管纯Python函数在实际中并不适用。作为数据科学家,我们可以暂且引进能够包含基本应用工具的黑盒子,是由我们有更多算法思想的同事参入所构建,但是我坚定的相信:当我们对所应用的数据的底层算法有更深的理解,我们也将会成为更优秀的从业者。