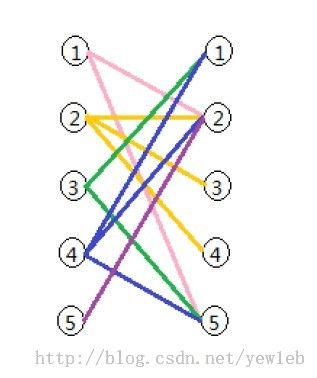
USCAO4.2 The Perfect Stall ，二分图最大匹配

题目地址：http://poj.org/problem?id=1274

题意：给你n 头牛，和m 个墙，每头牛有自己喜欢的墙，要求每堵墙只能有一头牛，求最多的匹配数。

分析：二分图的最大匹配

sample_input
5 5
2 2 5
3 2 3 4
2 1 5
3 1 2 5
1 2
sample_output
4

如下构成二分图，我们可以直接采用匈牙利算法。

给上图添加源点和汇点，就构成了网络流。把图构好后，就可以直接上模板了。

Code:

#include <cstdio>
#include <cstring>
#include <queue>
#include <vector>
#include <algorithm>
using namespace std;
const int maxn = 400 + 10;
const int INF = 1000000000;

struct Edge {
    int form, to, cap, flow;
};

struct Dinic {
    int n, m, s, t;
    vector<Edge> edges; //边表.edges[e]和edges[e^1]互为反向弧
    vector<int> G[maxn*maxn]; //邻接表，G[i][j]表示结点i的第j条边在e数组中的序号
    bool vis[maxn]; //BFS使用
    int d[maxn];  //从起点到i的距离
    int cur[maxn]; //当前弧指针

    void init(int n) {
        this->n = n;
        for (int i = 0; i <=n; i++) G[i].clear();
        edges.clear();
    }

    void AddEdge(int from, int to, int cap) {
        edges.push_back((Edge) {from, to, cap, 0});
        edges.push_back((Edge) {to, from, 0, 0});
        m = edges.size();
        G[from].push_back(m - 2);
        G[to].push_back(m - 1);
    }

    bool BFS() {//使用BFS计算出每一个点在残量网络中到t的最短距离d.
        memset(vis, 0, sizeof(vis));
        queue<int> Q;
        Q.push(s);
        vis[s] = 1;
        d[s] = 0;
        while (!Q.empty()) {
            int x = Q.front(); Q.pop();
            for (int i = 0; i < G[x].size(); i++) {
                Edge& e = edges[G[x][i]];
                if (!vis[e.to] && e.cap > e.flow) { //只考虑残量网络中的弧
                    vis[e.to] = 1;
                    d[e.to] = d[x] + 1;
                    Q.push(e.to);
                }
            }
        }
        return vis[t];
    }

    int DFS(int x, int a) {//使用DFS从S出发，沿着d值严格递减的顺序进行多路增广。
        if (x == t || a == 0) return a;
        int flow = 0, f;
        for (int& i = cur[x]; i < G[x].size(); i++) {
            Edge& e = edges[G[x][i]];
            if (d[x] + 1 == d[e.to] && (f = DFS(e.to, min(a, e.cap - e.flow))) > 0) {
                e.flow += f;
                edges[G[x][i] ^ 1].flow -= f;
                flow += f;
                a -= f;
                if (a == 0) break;
            }
        }
        return flow;
    }

    int Maxflow(int s, int t) {
        this->s = s; this->t = t;
        int flow = 0;
        while (BFS()) {
            memset(cur, 0, sizeof(cur));
            flow += DFS(s, INF);
        }
        return flow;
    }
};
Dinic g;
int n, m, s, t;

void make_graph() {
    int u, c, v;
    s = 0; t = n + m + 1;
    g.init(t);
    for (u = 1; u <= n; u++) {
        scanf("%d", &c);
        while (c--) {
            scanf("%d", &v);
            g.AddEdge(u, v + n, 1);
        }
    }
    for (u = 1; u <= n; u++) g.AddEdge(s, u, 1);
    for (u = 1; u <= m; u++) g.AddEdge(u + n, t, 1);

}

int main() {
    while (~scanf("%d%d", &n, &m)) {
        make_graph();
        int answer = g.Maxflow(s, t);
        printf("%d\n", answer);
    }
    return 0;
}