Machine Learning第七周笔记:支持向量机
博客已经迁移到Marcovaldo’s blog: http://marcovaldong.github.io/
今天在Cousera上学习了Machine Learning的第七周课程,这一周主要介绍了支持向量机(support vector machine),将学习笔记整理在下面。
Support Vector Machine
Large Margin Classification
Optimization Objective
我们通过逻辑回归来引出支持向量机。下图给出了逻辑回归的 hθ(x) 及其图像,我们将其中的 θTx 记为z。从training set中取出一组数据( x(i) , y(i) ),若有 y(i)=1 ,则我们应该得到 hθ(x)≈1 ,观察图像可知 θTx≫0 ;相反,若有 y(i)=0 ,则我们应该得到 hθ(x)≈0 ,观察图像可知 θTx<<0 。
我们来对逻辑回归的损失函数做一下分析,先在下面给出损失函数:
从training set中取出一组数据( x(i) , y(i) ),当 y(i)=1 时,损失函数的第二项为0,此时损失函数就变成了 −log11+e−z ,下图左侧为其图像。观察图像可以看到,当给z一个越来越大的值时,函数值变得越来越接近0。现在我们将函数调整为图像中红线对应的函数,叫做 cost1(z) 。当 y(i)=0 时,损失函数的第一项为0,此时损失函数就变成了 −(1−y)log(1−11+e−z) ,下图右侧为其图像。观察图像可以看到,当给z一个越来越小的值时,函数值变得越来越接近0。现在我们将函数调整为图像中红线对应的函数,叫做 cost0(z) 。那么以前求解hypothesis过程中用到的损失函数
调整为
此时得到的这个函数就是我们在支持向量机中用到的损失函数,求解此最小值问题得到的 θ 就是SVM的参数。对于给定的training set, 1m 是一个固定值,其值不影响最终求得的 θ ,所以我们将其省掉。
Large Margin Intuition
首先给出SVM的损失函数:
在逻辑回归中,我们的初衷是对于training set中的任何一组数据( x(i) , y(i) ),若 y(i)=1 ,则应该有 θTx>0 ,而在SVM中改成了 θTx>1 ;若 y(i)=0 ,则应该有 θTx<0 ,而在SVM中改成了 θTx<−1 。在SVM中多出来的这个1保证了其训练出来的参数\theta应该可以更好的拟合数据。
首先假设损失函数中的参数C是一个很大的值,我们来观察SVM是如何工作的。在对损失函数最小化的过程中,我们需要让 ∑mi=1[y(i)cost1(θTx(i))+(1−y(i))cost0(θTx(i))] 尽可能的趋近于0,此时我们的目标求解下面的最优化问题:
我们来看下图中的例子,图中的数据点是线性可分的,也就是说可以找到无数条直线(无数个超平面)来将两个类别完全分开。在下图中画出的三条decision boundary中,黑色直线所表示的那条要优于另外两条,因为它更robust地将两个类别分开了。图中两条蓝色直线分别表示两个类别中数据点与黑色decision boundary的最小距离,这一距离称作SVM中分类超平面关于training set的函数间隔。多个超平面也就对应多个函数间隔,我们将其中最大的函数间隔称作最大函数间隔。因此我们要做的就是找到最大间隔及其对应的最大间隔分离超平面,这个最大间隔分离超平面就是我们最终得到的hypothesis。
Mathematics Behind Large Margin Classification
这一小节我们来介绍SVM涉及到的一些数学,着有助于理解SVM中的最优化目标,帮助我们更快的找到最大间隔分离超平面。我们来回顾一下内积的概念。下图给出了两个二维向量并在坐标系中画出了他们。图中红色线段p表示向量v在向量u上的投影,两个向量的内积可以表示为
其中 ∥u∥=u21+u22−−−−−−√2 。而在第二个坐标系中,p是负的。
回到SVM,下图给出了要求解的优化问题,给出了 θTx(i) 的向量内积表示(这里我们取 x(i) 和、theta都是二维的):
所以原来的优化问题就转换成了下图所示的优化问题。,给定一个training set,下图给出了两个decision boundary。在图像中选择两个数据点( x(1) , y(1) )和( x(2) , y(2) ),画出分别对应的 p(1) 和 p(2) 。可以看到,左下侧中 p(1) 和 p(2) 的绝对值都很小,为了满足优化函数中的条件函数,会使得 ∥θ2∥ 的值变得很大,这恰好和我们的目标矛盾。而右下侧中 p(1) 和 p(2) 的绝对值都比较大,所以我们就可以选择一个更小的 ∥θ2∥ 来满足我们的目标。这就在数学上解释了右下侧的decision boundary为什么会优于左下侧的decison boundary。
Kernels
Kernel Ⅰ
这一小节我们来介绍处理线性不可分的数据集时经常用到的核技巧(kernel trick)。
在没有学习核技巧的情况下,我们需要引入一个多项式来表示decision boundary。
现在我们在坐标系中选定三个点 l(1) , l(2) , l(3) 作为landmark,由此出发去产生新的特征。至于选定landmark的标准我们后面再给出。具体的方法是对于给定的x有新的特征 f1=similarity(x,l(1)) , f2=similarity(x,l(2)) 和 f3=similarity(x,l(3)) ,下图给出了由gaussian kernel给出的 fi 。当然我们也可以选择其他的kernel来定义。当x很接近 l(1) 时(即有 x≈l(1) ),有 f1≈1 ;当x距离 l(1) 很远时,有 f1≈0 。对于另外两个特征也是一样,对于training set中任何一个数据都可以通过这种方式来获得新的特征值。
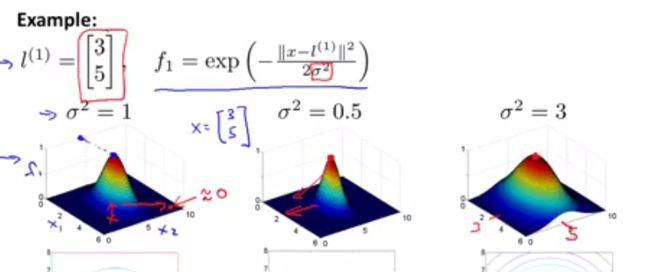
我们给出一个例子,如下图所示。给出了 l(1) , f1 的定义,图像中的横纵坐标为x的两个维度,第三个维度代表新的特征值。只有当 x=l(1) 时,其对应的新特征值 f1 达到1,随着x越来越远离 l(1) ,x对应的新特征值逐渐趋向于0。比较 σ2 的不同取值下的三维图像可知,随着 σ2 的增大, f1 的取值在 l(1) 的周围变化得快,图像变得尖锐;随着 σ2 的减小, f1 的取值在 l(1) 的周围变化得慢,图像变得平缓。
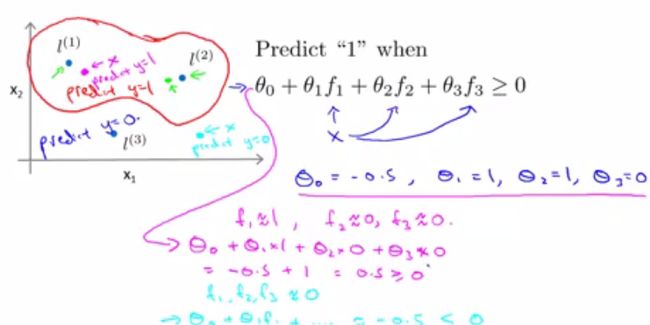
现在我们将前面的东西应用到分类上,假设现在我们的hypothesis如下图所给公式,其中 θ=(−0.5,1,1,0)T 。我们在图像中选出3个数据点,分别计算它们和3个landmarks的相似度,带入hypothesis得到对数据点的分类。利用这种方法,我们可以把坐标系中的数据点分成两类:红色曲线包围的是一类,其余的是一类。
Kernel Ⅱ
现在我们介绍如何选取landmark。下图给出了具体过程:给定training set,其中包含m个数据点。选择m个landmark,其中 l(i)=x(i) 。
下图给出了使用了kernel的SVM:
上面的方法不适用于很大的training set,例如数据量m为5000,那就会有5000个landmark,相应的参数 θ 的维度也是5000,求解参数则需要特别大的计算量。现在我们来讨论一下参数C(=\frac{1}{\lambda})和Gaussian kernel中 σ2 的选取:
SVMs in Practice
Using An SVM
这一小节我们介绍如何实际应用SVM。现在在不同的语言环境下已经有很多求解SVM参数的包供我们使用,现在我们来讨论一下C和kernel的选取。(linear kernel是指我们在使用SVM时没用引入kernel)当我们选取Gaussian kernel时,我们考虑 σ2 的选取,以做到对bias-variance的权衡:当 σ2 取值比较大时,hypothesis偏向于high bias;当 σ2 取值较小时,hypothesis倾向于high variance。当特征值不多,training set较大时,Gaussian kernel可能是个较好的选择。当模型含有的特征数量很大时,核函数的计算量变得很大,这时就不适合用Gaussian kernel了。
并不是所有的similarity function都能构造有效的kernel,kernel需要满足Mercer’s Theorem以保证SVM中的优化问题有解。这里给出了使用率较高的几种kernel:polynomial kernel/string kernel/chi-square kernel/histogram,但最常用的还是linear kernel和Gaussian kernel。
Andrew Ng是从逻辑回归出发去介绍的SVM,所以这里的SVM看起来更像是逻辑回归的一个变形,我会在以后的文章中给出对SVM的介绍。