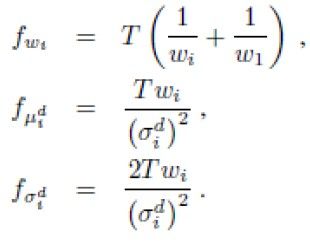机器学习笔记——Fisher vector coding
Fisher Kernels原理
模式分类的技术主要可以划分为生成式和判别式两大类。生成式模型关注类条件概率的建模,判别式模型则直接关注问题的本身——分类。这也解释了判别式模型相对于生成式模型理论上的优越性。尽管如此,生成式模型也具有判别式模型不具备的许多特性,使生成式模型被广泛使用。如生成式模型可以处理长度不一的数据。
其中,Fisher kernels的引入结合了生成式模型和判别式模型的优点。首先我们假定![]() 是概率密度函数(pdf),其参数为
是概率密度函数(pdf),其参数为![]() 。于是一个含
。于是一个含![]() 个描述子的样本可以用如下似然函数的梯度向量表示(在此
个描述子的样本可以用如下似然函数的梯度向量表示(在此![]() 可以理解为提取了20个SIFT角点的图像,注意,不同的图像
可以理解为提取了20个SIFT角点的图像,注意,不同的图像![]() 通常提取到的SIFT的数量
通常提取到的SIFT的数量![]() 可以不一样):
可以不一样):
(1)
令![]() ,公式(1)又可以表示为
,公式(1)又可以表示为
(2)
直觉上我们可以发现,对数似然函数的梯度描述了模型参数为更好地拟合当前样本参数应当改变的方向。也就是说,我们将一个长度不定的样本![]() 转换成了一个具有固定长度的梯度向量。其中,梯度特征向量的维度等于模型参数的个数。
转换成了一个具有固定长度的梯度向量。其中,梯度特征向量的维度等于模型参数的个数。
上述梯度向量可以作为样本的特征,用于任何的判别式分类器中。可是,不少采用了内积的判别式分类器要求我们输入的必须是归一化的特征向量。为实现梯度特征向量的归一化,我们可以利用Fisher信息矩阵:
![]() (3)
(3)
归一化后的梯度向量可以表示为:
![]() (4)
(4)
自然而然地,我们可以想到,用以下的Fisher kernel 来衡量样本X和样本Y之间的距离,即表示两样本间的相似度:
![]() 。 (5)
。 (5)
Fisher Vector(FV)在图像上的应用
假设是从一张图像上提取到的 (6)
即FV是图像上各个的局部描述子的归一化梯度统计量 ![]() 之和。
之和。
混合高斯模型(GMM)的情形
假设以上的分布服从混合高斯模型,模型的参数为![]() ,则有
,则有
(7)
其中,
在此,我们假定协方差矩阵为对角矩阵。由贝叶斯公式可知,描述子![]() 属于第
属于第![]() 个高斯模型的概率为:
个高斯模型的概率为:
,如图1所示。
图1 公式(8)图示
公式(1)关于GMM各梯度分量为
由文献[1]可得Fisher信息矩阵的近似解为
又由公式(6)可得归一化的FV
即
FV和BoW以及VLAD的关系
假如混合高斯模型的数量为K(即码本大小为K),局部特征描述子的长度为D。BoW得到K维直方图向量。公式1关于每个高斯模型的参数求导可得2D+1维向量,总共K个高斯模型,因此可得(2D+1)K维特征向量,又因为GMM模型权值之和为1带来一维冗余,因此FV得到(2D+1)K-1维直方图向量。
由以上分析可知,给定同样大小的码本,FV得到的直方图向量维数一般远高于BoW。亦即,若要生成类似大小的直方图向量,FV需要更小的码本,即更小的计算成本。
从局部描述子到FV算法流程
参考论文
[1] F. Perronnin and C. Dance. Fisher kenrels on visual vocabularies for image categorizaton. In Proc. CVPR, 2006.
[2] Florent Perronnin, Jorge Sánchez, and Thomas Mensink. Improving the fisher kernel for large-scale image classification. In Proc. ECCV, 2010.
参考ppt
[1] http://people.rennes.inria.fr/Herve.Jegou/courses/2012_cpvr_tutorial/4-new-patch-agggregation.pptx.pdf
[2] http://www.cs.ucf.edu/courses/cap6412/spr2014/papers/Fisher-Vector-Encoding.pdf
fisher information matrix
http://en.wikipedia.org/wiki/Fisher_information
http://www.ii.pwr.wroc.pl/~tomczak/PDF/[JMT]Fisher_inf.pdf
代码:
http://www.vlfeat.org/api/fisher.html