字典树-字符串处理

Trie树概念

别称：单词查找树、字典树
结构：树形结构，哈希树的变种
应用：统计、排序、保存大量字符串
优点：利用公共前缀，减少查询时间和比较次数

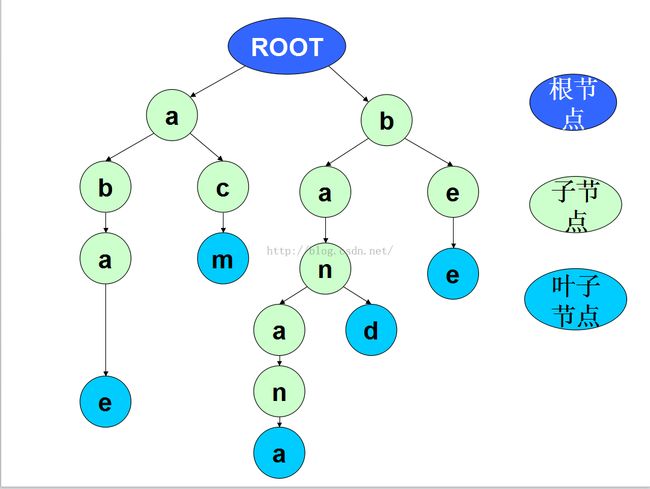
树的概念

节点：根节点、父节点、子节点、叶子节点
关系：父子（前驱后继）、兄弟（相同父节点）

Trie树特点

空间换时间
每一个节点都有至少26个子节点（对于单词）
插入、查询时间复杂度都为O(len)
排序按照Trie树先序遍历

节约空间
保存大量单词时候，相同前缀的空间共用

Trie树性质

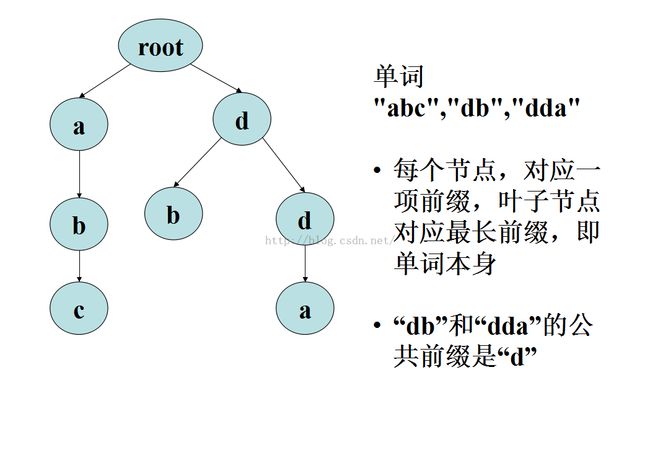
除根节点外，每个节点包含一个字符
从根节点到某一结点的路径，为对应节点的字符串
每个节点的所有子节点包含的字符均不同

Trie树的实现

1 Trie树定义

指向子节点的指针
当前节点的值

struct Trie                                // 定义Trie树节点结构体
{
    int value;                             // 节点的值
    Trie *child[26];                  // 指向的子节点的指针
    Trie()                                    // 构造函数初始化
    {
        value = 0;
        memset(child, NULL, sizeof(child));
    }
} *root;                                   // 根节点指针

2 插入过程

从根节点开始，按照字母对应节点不断向下
直到单词结束，在该节点上记录单词信息

void Insert(char str[])                // 插入字符串str
{
    Trie *x = root;                        // 从根节点开始
    for(int i = 0; str[i]; i++)         // 逐个插入
    {
        int d = str[i] - 'a';
        // 若子节点不存在，则new出对应节点
        if(x->child[d] == NULL) 
            x->child[d] = new Trie;
        x = x->child[d];                 // 转成对应子树
    }
    x->vlaue ++;                         // 表示该单词出现次数
}

3 查找过程

从根节点开始搜索
得到第一个字母节点后，转到对应子树
在相应子树继续搜索下一个字母
重复上述操作，直到单词结束，读取节点信息

int Search(char str[])                 // 查找字符串str
{
    Trie *x = root;                        // 从根节点开始
    for(int i = 0; str[i]; i++)   
    {
        int d = str[i] - 'a';
        if(x->child[d] == NULL)   // 查找失败，直接退出
            return 0;
        x = x->child[d];                  // 转成对应子树
    }
    return x->vlaue;                    // 查找成功，返回节点的值
}

释放空间

void Deal(Trie*x)                    // 释放x为根的子树
{ 
    if(x == NULL)
        return ;
    for(int i = 0; i<26; i++)        // 释放x的所有子节点
    {
        if(x->child[i] != NULL)
            Deal(x->child[i]);
    }
    delete x;                               // 释放x节点空间
}

补充：

动态创建新节点（new）
释放空间(delete)，否则会后组数据影响而WA
动态申请新节点耗时太多，数据量大容易TLE
采用静态方式
注意作为“内存”的数组大小，否则容易RE