素数测试(2)
4.wilson检测(威尔逊检测)
读过数论的朋友一定看过wilson算法,在数论中,威尔逊定理给出了判定一个自然是否为素数的充分必要条件,即:当且仅当p为素数时:( p -1 )! ≡ -1 ( mod p )
如果您没接触过数论,帮您解释下这个式子是啥意思,(mod p)叫同余 意思就是除以p后余数相等,可以把上述式子理解为当且仅当p为素数时,[(p-1)!+1]%p == 0
显然这个算法时间复杂度和需要数据类型的表示范围之大都是无法回避的,实际操作不可行,理论价值非常高。
代码清单:
public class SuXingCeShi {
public static void main(String[] args) {
int n = 100;
SuXingCeShi robot = new SuXingCeShi();
robot.wilson(n);
}
public void wilson(int n){
for(int i = 2; i <= n; i++)
if(isPrimeFromWilson(i))
System.out.print(i + " ");
System.out.println();
}
private boolean isPrimeFromWilson(int m) {
long temp = 1;
int i = m-1;
while(i >= 1){
temp *= i;
i--;
}
return (temp+1) % m == 0;
}
}
5.费马查表法
首先介绍一个数论中非常非常重要的一个定理-----费马小定理
假如a是一个整数,p是一个素数,那么![]() (0 < a < p)
(0 < a < p)
换句话说也就是:如果p是一个素数,且0<a<p,则a^(p-1)%p=1 但是费马小定理是判断素数的必要条件,当a=2时候,有一类伪素数数,它们满足费马小定理,但其本身却不是素数。它们有无穷个,最小的伪素数是341,统计表明前10亿个数中有50847534个素数,满足2^(p-1)%p = 1的伪素数一共有5597,出错概率非常之低,所以我们可以根据我们的需求建一表伪素数表,算出素数看是否存在这张表里(可以二分,hash,trie)
好了,具备了以上知识我们想想费马小定理的函数该怎么写?
如果直接算2^(p-1)数的表示范围很头疼,于是我们可以利用这个迭代公式来计算
代码清单:
int runFermatPower(int a, int b, int n) {//返回a^b mod n
int result = 1;
for (int i = 0; i < b; i++) {
result *= a;
result %= n;
}
return result;
}
int runFermatPower(int a, int b, int n)// d≡a^b mod n
{
int result = 1;
while (b > 0) {
if ((b & 1) == 1)
result = (result * a) % n;
b >>= 1;
a = (a * a) % n;
}
return result;
}
首先我们先把问题简化一下,看看如何快速求a^b.
先看看我们熟知的两个数学公式:
a^(2c) = (a^c)^2;
a^(2c+1) = a*((a^c)^2);
我们就利用这两个数学公式来解决这个问题,比如a=3,b=13时,我们把b写成二进制的形式13(10)=1101(2),我们从低位到高位运算,每运算一位可以将b右移一位,上面的例子可以转化成3^13 = 3^1 * 3^4 * 3^8,结合上面的两个数学公式我们可以写出如下的代码:
代码清单:
public class MyPow {
public static void main(String[] args){
int a = 3;
int b = 13;
int m = pow(a,b);
System.out.println(m);
}
private static int pow(int a, int b) {
int result = 1;
while(b > 0){
if((b & 1) == 1)//b的某位上为1时才累乘
result *= a;
a *= a;//数学公式所得
b >>= 1;//右移1位
}
return result;
}
}
如上面的叙述叙述中可以看出快速pow算法的时间复杂度 取决于b的二进制位数 ,而传统的一位一位累乘的pow算法的时间复杂度 取决于b的大小 ,例如上述例子中,两种算法的运算次数分别为4次,和13次。随着b的增大,效率上的差距是显然的。
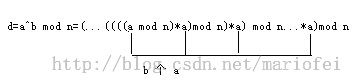
下面进入我们的主题---大数模幂运算快速算法(a^b % m)
要计算这个,我们首先还要知道一个数学公式:
a^b % m = (...((a % m) * a) % m) ......* a) % m其中a%m有b个
下面我还用上面b=13的例子,利用这个公式来证明下
a^13 % m = ((a^8) % m) * ((a^4) % m) * ((a^1) % m)
证明:
由a^b % m = (...((a % m) * a) % m) ......* a) % m其中a%m有b个得
a^8 % m = (...((a % m) * a) % m) ......* a) % m其中a%m有8个
a^4 % m = (...((a % m) * a) % m) ......* a) % m其中a%m有4个
a^1 % m = (...((a % m) * a) % m) ......* a) % m 其中a%m有1个
所以((a^8) % m) * ((a^4) % m) * ((a^1) % m) = (...((a % m) * a) % m) ......* a) % m 其中a%m有13个 = a^13 % m ;
证毕。
由上面我们证明的公式和第一个pow的例子,容易写出代码如下:
int runFermatPow(int a, int b, int m){
int result = 1;
while (b > 0) {
if ((b & 1) == 1)
result = (result * a);
a = (a * a) % m;
b >>= 1;
}
return result % m;
}
解释:当b=1101(2)时,从第1位开始result累乘,a = (a*a)%m加上循环可以看成表达式(a%m)^2 % m....因为(a%m)^2 % m = a^2 % m ,所以我们可以把a^13%m看成((a^1) % m) ,((a^4) % m) ,((a^8) % m)的累乘,最后对m取模。
但累乘很容易造成溢出,所以我们可以把代码改成如下形式:
int runFermatPow(int a, int b, int m){
int result = 1;
while (b > 0) {
if ((b & 1) == 1)
result = (result * a) % m;
a = (a * a) % m;
b >>= 1;
}
return result;
}
public void femat(int n){
for(int i = 2; i <= n; i++){
if(runFermatPower(2, n-1, n) != 1){
if(i不在伪素数表中)
输出i;
}
}
}