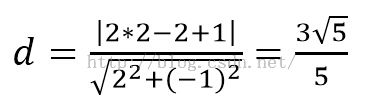SVM初学
一、 一点基础数学知识
现在硕士都快毕业了，反而将自己的许多数学知识忘的差不多了，所以，现在决心再捡起来，以补齐自己的数学短板，为以后的研究做好铺垫吧。现在结合自己学习SVM、MLC、ANN等机器学习方法来回顾以前的数学知识以及补充新的数学知识。
在SVM中，首先面临的问题是计算样本点到分类超平面的距离，现在就从最简单的点到直线的距离、点到平面的距离等内容开始回顾。
1） 点到直线的距离计算公式
假设直线L的方程为：
那么，点（x0,y0）到直线L的距离为d
如点（2,2）到直线2x-y+1=0的距离为：
几何示意图如下：
2)点到平面的距离
假设平面P的方程为
,则点（X0,Y0,Z0）到平面P的距离d为：
几何示意图如下。
对于高维空间，假设存在超平面f(x)=W*X+b，那么样本点到超平面的相对距离距离可以用
来表示。但是，这并不是严格的定义。在确切的描述高维空间中，点到超平面的距离之前，首先要引入向量、范数等数学知识加以描述。
3）向量内积（点积或者数量积）
假设有a=[a0,a1,a2,a3,…,an],和向量b=[b0,b1,b2,b3,…,bn]，则向量a与向量b之间的内积为：a.b=a0b0+a1b1+a2b2+a3b3+…+anbn=|a||b|cosθ=a*bT, θ为向量a与向量b之间的夹角,T表示矩阵转置运算.
4）向量叉积（向量叉乘）
a×b=|a||b|sinθ,θ为向量a与向量b之间的夹角。其运算结果是一个向量而不是标量。假设a=(ax,ay,az),b=(bx,by,bz)
为了便于记忆，利用三阶行列式，写成
则:
a×b=（aybz-azby）i+(azbx-axbz)j+(axby-aybx)k=( aybz-azby, azbx-axbz,axby-aybx)
5）范数
定义：范数(norm)是数学中的一种基本概念，在泛函分析中，范数是一种定义在赋范线性空间中函数，满足相应条件后的函数都可以被称为范数。是具有“长度”概念的函数。在线性代数、泛函分析及相关的数学领域，范函是一个函数，其为矢量空间内的所有矢量赋予非零的正长度或大小。半范数反而可以为非零的矢量赋予零长度。
对于向量v,向量的长度（范数）为非负数
假设v是 实数域中的向量，
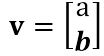
,如果v与二维平面上的点（a，b）对应，那么范数
的几何意义为二维平面上原点到点（a,b）的直线距离。
有了范数的概念，我们便能推导点到超平面的距离（SVM中的几何间隔）。
上图所示，对于一个点x ，令其垂直投影到超平面上的对应的为x0 ，由于w是垂直于超平面的一个向量（即超平面的一个法向量）， 为样本x到分类间隔的距离，我们有：
其中，
即为范数。
即为超平面的单位法向量。我们在此将上式代入超平面方程进行推导：
因为，x0为超平面上的点，满足f(x0)=0
因此：
又因为 
，因此：
至此，我们推导了点到超平面的几何距离。但是，回到SVM中，由于SVM中超平面存在方向性，即在超平面的左侧或者右侧，其函数值存在正负。因此，我们还需要对上述的几何距离的定义加以约束。通俗点说，就是f(x)的取值有正有负，但距离必须是正的，所以，在SVM中，由于采用类别标签（+1，-1）来表示分类的类别属性，因此定义
因此，在SVM中，其几何间距（Geometrical Margin）
从这也可以看出，对于二分类问题，SVM为什么习惯将类别标签默认为（+1，-1）。