HDU 5666 Segment——BestCoder Round #80
Segment
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Others)
Total Submission(s): 0 Accepted Submission(s): 0
Problem Description
Silen August does not like to talk with others.She like to find some interesting problems.
Today she finds an interesting problem.She finds a segment x+y=q .The segment intersect the axis and produce a delta.She links some line between (0,0) and the node on the segment whose coordinate are integers.
Please calculate how many nodes are in the delta and not on the segments,output answer mod P.
Today she finds an interesting problem.She finds a segment x+y=q .The segment intersect the axis and produce a delta.She links some line between (0,0) and the node on the segment whose coordinate are integers.
Please calculate how many nodes are in the delta and not on the segments,output answer mod P.
Input
First line has a number,T,means testcase number.
Then,each line has two integers q,P.
q is a prime number,and 2≤q≤1018,1≤P≤1018,1≤T≤10.
Then,each line has two integers q,P.
q is a prime number,and 2≤q≤1018,1≤P≤1018,1≤T≤10.
Output
Output 1 number to each testcase,answer mod P.
Sample Input
1 2 107
Sample Output
0
Source
BestCoder Round #80
/************************************************************************/
附上该题对应的中文题
Segment
Time Limit: 2000/1000 MS (Java/Others)
Memory Limit: 65536/65536 K (Java/Others)
问题描述
Rivendell非常神,喜欢研究奇怪的问题. 今天他发现了一个有趣的问题.找到一条线段x+y=q,令它和坐标轴在第一象限围成了一个三角形,然后画线连接了坐标原点和线段上坐标为整数的格点. 请你找一找有多少点在三角形的内部且不是线段上的点,并将这个个数对P取模后告诉他.
输入描述
第一行一个数T,为测试数据组数. 接下来每一行两个数q,P,意义如题目中所示. q是质数且q≤1018,1≤P≤1018,1≤T≤10.
输出描述
对每组数据,输出点的个数模P后的值.
输入样例
1 2 107
输出样例
0
/****************************************************/
出题人的解题思路:
1002
考虑一条以(0,0)为起点,(x,y)为终点的线段上格点的个数(不包含端点时),一定是gcd(x,y)−1,这个很显然吧.
然后整个网格图范围内的格点数目是2q∗(q−1).
所以答案就是2q∗(q−1)− 所有线段上的格点的个数.
因为gcd(a,b)=gcd(a,b−a) (b>a),所以gcd(x,y)=gcd(x,p−x)=gcd(x,p),p是质数,所以gcd(x,y)=1,所以线段上都没有格点,所以答案就是2q∗(q−1).
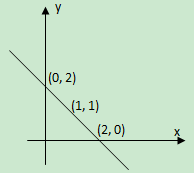
首先,题目描述的三角形是由x轴,y轴与直线x+y=q围成的,故点(0,q)与点(q,0)即为三角形的两个顶点
现要求有多少个整数格点落在三角形内(不包括边),很容易想到要满足条件q>2(即q<=2时三角形内不存在整数格点),如图就是三角形内不存在整数格点的一个例子
而当q>2之后,三角形内的整数格点数count为:
/*Sherlock and Watson and Adler*/
/*
+,-,*,/,% 可直接使用.
CIN读入
bignum数据类型
*/
#include<iostream>
#include<string.h>
#include<stdio.h>
#include<iostream>
using namespace std;
#define DIGIT 4
#define DEPTH 10000
#define MAX 100
typedef int bignum_t[MAX+1];
int read(bignum_t a,istream& is=cin){
char buf[MAX*DIGIT+1],ch;
int i,j;
memset((void*)a,0,sizeof(bignum_t));
if (!(is>>buf)) return 0;
for (a[0]=strlen(buf),i=a[0]/2-1;i>=0;i--)
ch=buf[i],buf[i]=buf[a[0]-1-i],buf[a[0]-1-i]=ch;
for (a[0]=(a[0]+DIGIT-1)/DIGIT,j=strlen(buf);j<a[0]*DIGIT;buf[j++]='0');
for (i=1;i<=a[0];i++)
for (a[i]=0,j=0;j<DIGIT;j++)
a[i]=a[i]*10+buf[i*DIGIT-1-j]-'0';
for (;!a[a[0]]&&a[0]>1;a[0]--);
return 1;
}
void write(const bignum_t a,ostream& os=cout){
int i,j;
for (os<<a[i=a[0]],i--;i;i--)
for (j=DEPTH/10;j;j/=10)
os<<a[i]/j%10;
}
int comp(const bignum_t a,const bignum_t b){
int i;
if (a[0]!=b[0])
return a[0]-b[0];
for (i=a[0];i;i--)
if (a[i]!=b[i])
return a[i]-b[i];
return 0;
}
int comp(const bignum_t a,const int b){
int c[12]={1};
for (c[1]=b;c[c[0]]>=DEPTH;c[c[0]+1]=c[c[0]]/DEPTH,c[c[0]]%=DEPTH,c[0]++);
return comp(a,c);
}
int comp(const bignum_t a,const int c,const int d,const bignum_t b){
int i,t=0,O=-DEPTH*2;
if (b[0]-a[0]<d&&c)
return 1;
for (i=b[0];i>d;i--){
t=t*DEPTH+a[i-d]*c-b[i];
if (t>0) return 1;
if (t<O) return 0;
}
for (i=d;i;i--){
t=t*DEPTH-b[i];
if (t>0) return 1;
if (t<O) return 0;
}
return t>0;
}
void add(bignum_t a,const bignum_t b){
int i;
for (i=1;i<=b[0];i++)
if ((a[i]+=b[i])>=DEPTH)
a[i]-=DEPTH,a[i+1]++;
if (b[0]>=a[0])
a[0]=b[0];
else
for (;a[i]>=DEPTH&&i<a[0];a[i]-=DEPTH,i++,a[i]++);
a[0]+=(a[a[0]+1]>0);
}
void add(bignum_t a,const int b){
int i=1;
for (a[1]+=b;a[i]>=DEPTH&&i<a[0];a[i+1]+=a[i]/DEPTH,a[i]%=DEPTH,i++);
for (;a[a[0]]>=DEPTH;a[a[0]+1]=a[a[0]]/DEPTH,a[a[0]]%=DEPTH,a[0]++);
}
void sub(bignum_t a,const bignum_t b){
int i;
for (i=1;i<=b[0];i++)
if ((a[i]-=b[i])<0)
a[i+1]--,a[i]+=DEPTH;
for (;a[i]<0;a[i]+=DEPTH,i++,a[i]--);
for (;!a[a[0]]&&a[0]>1;a[0]--);
}
void sub(bignum_t a,const int b){
int i=1;
for (a[1]-=b;a[i]<0;a[i+1]+=(a[i]-DEPTH+1)/DEPTH,a[i]-=(a[i]-DEPTH+1)/DEPTH*DEPTH,i++);
for (;!a[a[0]]&&a[0]>1;a[0]--);
}
void sub(bignum_t a,const bignum_t b,const int c,const int d){
int i,O=b[0]+d;
for (i=1+d;i<=O;i++)
if ((a[i]-=b[i-d]*c)<0)
a[i+1]+=(a[i]-DEPTH+1)/DEPTH,a[i]-=(a[i]-DEPTH+1)/DEPTH*DEPTH;
for (;a[i]<0;a[i+1]+=(a[i]-DEPTH+1)/DEPTH,a[i]-=(a[i]-DEPTH+1)/DEPTH*DEPTH,i++);
for (;!a[a[0]]&&a[0]>1;a[0]--);
}
void mul(bignum_t c,const bignum_t a,const bignum_t b){
int i,j;
memset((void*)c,0,sizeof(bignum_t));
for (c[0]=a[0]+b[0]-1,i=1;i<=a[0];i++)
for (j=1;j<=b[0];j++)
if ((c[i+j-1]+=a[i]*b[j])>=DEPTH)
c[i+j]+=c[i+j-1]/DEPTH,c[i+j-1]%=DEPTH;
for (c[0]+=(c[c[0]+1]>0);!c[c[0]]&&c[0]>1;c[0]--);
}
void mul(bignum_t a,const int b){
int i;
for (a[1]*=b,i=2;i<=a[0];i++){
a[i]*=b;
if (a[i-1]>=DEPTH)
a[i]+=a[i-1]/DEPTH,a[i-1]%=DEPTH;
}
for (;a[a[0]]>=DEPTH;a[a[0]+1]=a[a[0]]/DEPTH,a[a[0]]%=DEPTH,a[0]++);
for (;!a[a[0]]&&a[0]>1;a[0]--);
}
void mul(bignum_t b,const bignum_t a,const int c,const int d){
int i;
memset((void*)b,0,sizeof(bignum_t));
for (b[0]=a[0]+d,i=d+1;i<=b[0];i++)
if ((b[i]+=a[i-d]*c)>=DEPTH)
b[i+1]+=b[i]/DEPTH,b[i]%=DEPTH;
for (;b[b[0]+1];b[0]++,b[b[0]+1]=b[b[0]]/DEPTH,b[b[0]]%=DEPTH);
for (;!b[b[0]]&&b[0]>1;b[0]--);
}
void div(bignum_t c,bignum_t a,const bignum_t b){
int h,l,m,i;
memset((void*)c,0,sizeof(bignum_t));
c[0]=(b[0]<a[0]+1)?(a[0]-b[0]+2):1;
for (i=c[0];i;sub(a,b,c[i]=m,i-1),i--)
for (h=DEPTH-1,l=0,m=(h+l+1)>>1;h>l;m=(h+l+1)>>1)
if (comp(b,m,i-1,a)) h=m-1;
else l=m;
for (;!c[c[0]]&&c[0]>1;c[0]--);
c[0]=c[0]>1?c[0]:1;
}
void div(bignum_t a,const int b,int& c){
int i;
for (c=0,i=a[0];i;c=c*DEPTH+a[i],a[i]=c/b,c%=b,i--);
for (;!a[a[0]]&&a[0]>1;a[0]--);
}
void sqrt(bignum_t b,bignum_t a){
int h,l,m,i;
memset((void*)b,0,sizeof(bignum_t));
for (i=b[0]=(a[0]+1)>>1;i;sub(a,b,m,i-1),b[i]+=m,i--)
for (h=DEPTH-1,l=0,b[i]=m=(h+l+1)>>1;h>l;b[i]=m=(h+l+1)>>1)
if (comp(b,m,i-1,a)) h=m-1;
else l=m;
for (;!b[b[0]]&&b[0]>1;b[0]--);
for (i=1;i<=b[0];b[i++]>>=1);
}
int length(const bignum_t a){
int t,ret;
for (ret=(a[0]-1)*DIGIT,t=a[a[0]];t;t/=10,ret++);
return ret>0?ret:1;
}
int digit(const bignum_t a,const int b){
int i,ret;
for (ret=a[(b-1)/DIGIT+1],i=(b-1)%DIGIT;i;ret/=10,i--);
return ret%10;
}
int zeronum(const bignum_t a){
int ret,t;
for (ret=0;!a[ret+1];ret++);
for (t=a[ret+1],ret*=DIGIT;!(t%10);t/=10,ret++);
return ret;
}
void comp(int* a,const int l,const int h,const int d){
int i,j,t;
for (i=l;i<=h;i++)
for (t=i,j=2;t>1;j++)
while (!(t%j))
a[j]+=d,t/=j;
}
void convert(int* a,const int h,bignum_t b){
int i,j,t=1;
memset(b,0,sizeof(bignum_t));
for (b[0]=b[1]=1,i=2;i<=h;i++)
if (a[i])
for (j=a[i];j;t*=i,j--)
if (t*i>DEPTH)
mul(b,t),t=1;
mul(b,t);
}
void combination(bignum_t a,int m,int n){
int* t=new int[m+1];
memset((void*)t,0,sizeof(int)*(m+1));
comp(t,n+1,m,1);
comp(t,2,m-n,-1);
convert(t,m,a);
delete []t;
}
void permutation(bignum_t a,int m,int n){
int i,t=1;
memset(a,0,sizeof(bignum_t));
a[0]=a[1]=1;
for (i=m-n+1;i<=m;t*=i++)
if (t*i>DEPTH)
mul(a,t),t=1;
mul(a,t);
}
#define SGN(x) ((x)>0?1:((x)<0?-1:0))
#define ABS(x) ((x)>0?(x):-(x))
int read(bignum_t a,int &sgn,istream& is=cin){
char str[MAX*DIGIT+2],ch,*buf;
int i,j;
memset((void*)a,0,sizeof(bignum_t));
if (!(is>>str)) return 0;
buf=str,sgn=1;
if (*buf=='-') sgn=-1,buf++;
for (a[0]=strlen(buf),i=a[0]/2-1;i>=0;i--)
ch=buf[i],buf[i]=buf[a[0]-1-i],buf[a[0]-1-i]=ch;
for (a[0]=(a[0]+DIGIT-1)/DIGIT,j=strlen(buf);j<a[0]*DIGIT;buf[j++]='0');
for (i=1;i<=a[0];i++)
for (a[i]=0,j=0;j<DIGIT;j++)
a[i]=a[i]*10+buf[i*DIGIT-1-j]-'0';
for (;!a[a[0]]&&a[0]>1;a[0]--);
if (a[0]==1&&!a[1]) sgn=0;
return 1;
}
struct bignum{
bignum_t num;
int sgn;
public:
inline bignum(){memset(num,0,sizeof(bignum_t));num[0]=1;sgn=0;}
//inline int operator!(){return num[0]==1&&!num[1];}
inline bignum& operator=(const bignum& a){memcpy(num,a.num,sizeof(bignum_t));sgn=a.sgn;return *this;}
inline bignum& operator=(const int a){memset(num,0,sizeof(bignum_t));num[0]=1;sgn=SGN(a);add(num,sgn*a);return *this;};
inline bignum& operator+=(const bignum& a){if(sgn==a.sgn)add(num,a.num);else if(sgn&&a.sgn){int ret=comp(num,a.num);if(ret>0)sub(num,a.num);else if(ret<0){bignum_t t;
memcpy(t,num,sizeof(bignum_t));memcpy(num,a.num,sizeof(bignum_t));sub(num,t);sgn=a.sgn;}else memset(num,0,sizeof(bignum_t)),num[0]=1,sgn=0;}else if(!sgn)memcpy(num,a.num,sizeof(bignum_t)),sgn=a.sgn;return *this;}
inline bignum& operator+=(const int a){if(sgn*a>0)add(num,ABS(a));else if(sgn&&a){int ret=comp(num,ABS(a));if(ret>0)sub(num,ABS(a));else if(ret<0){bignum_t t;
memcpy(t,num,sizeof(bignum_t));memset(num,0,sizeof(bignum_t));num[0]=1;add(num,ABS(a));sgn=-sgn;sub(num,t);}else memset(num,0,sizeof(bignum_t)),num[0]=1,sgn=0;}else if(!sgn)sgn=SGN(a),add(num,ABS(a));return *this;}
inline bignum operator+(const bignum& a){bignum ret;memcpy(ret.num,num,sizeof(bignum_t));ret.sgn=sgn;ret+=a;return ret;}
inline bignum operator+(const int a){bignum ret;memcpy(ret.num,num,sizeof(bignum_t));ret.sgn=sgn;ret+=a;return ret;}
inline bignum& operator-=(const bignum& a){if(sgn*a.sgn<0)add(num,a.num);else if(sgn&&a.sgn){int ret=comp(num,a.num);if(ret>0)sub(num,a.num);else if(ret<0){bignum_t t;
memcpy(t,num,sizeof(bignum_t));memcpy(num,a.num,sizeof(bignum_t));sub(num,t);sgn=-sgn;}else memset(num,0,sizeof(bignum_t)),num[0]=1,sgn=0;}else if(!sgn)add(num,a.num),sgn=-a.sgn;return *this;}
inline bignum& operator-=(const int a){if(sgn*a<0)add(num,ABS(a));else if(sgn&&a){int ret=comp(num,ABS(a));if(ret>0)sub(num,ABS(a));else if(ret<0){bignum_t t;
memcpy(t,num,sizeof(bignum_t));memset(num,0,sizeof(bignum_t));num[0]=1;add(num,ABS(a));sub(num,t);sgn=-sgn;}else memset(num,0,sizeof(bignum_t)),num[0]=1,sgn=0;}else if(!sgn)sgn=-SGN(a),add(num,ABS(a));return *this;}
inline bignum operator-(const bignum& a){bignum ret;memcpy(ret.num,num,sizeof(bignum_t));ret.sgn=sgn;ret-=a;return ret;}
inline bignum operator-(const int a){bignum ret;memcpy(ret.num,num,sizeof(bignum_t));ret.sgn=sgn;ret-=a;return ret;}
inline bignum& operator*=(const bignum& a){bignum_t t;mul(t,num,a.num);memcpy(num,t,sizeof(bignum_t));sgn*=a.sgn;return *this;}
inline bignum& operator*=(const int a){mul(num,ABS(a));sgn*=SGN(a);return *this;}
inline bignum operator*(const bignum& a){bignum ret;mul(ret.num,num,a.num);ret.sgn=sgn*a.sgn;return ret;}
inline bignum operator*(const int a){bignum ret;memcpy(ret.num,num,sizeof(bignum_t));mul(ret.num,ABS(a));ret.sgn=sgn*SGN(a);return ret;}
inline bignum& operator/=(const bignum& a){bignum_t t;div(t,num,a.num);memcpy(num,t,sizeof(bignum_t));sgn=(num[0]==1&&!num[1])?0:sgn*a.sgn;return *this;}
inline bignum& operator/=(const int a){int t;div(num,ABS(a),t);sgn=(num[0]==1&&!num[1])?0:sgn*SGN(a);return *this;}
inline bignum operator/(const bignum& a){bignum ret;bignum_t t;memcpy(t,num,sizeof(bignum_t));div(ret.num,t,a.num);ret.sgn=(ret.num[0]==1&&!ret.num[1])?0:sgn*a.sgn;return ret;}
inline bignum operator/(const int a){bignum ret;int t;memcpy(ret.num,num,sizeof(bignum_t));div(ret.num,ABS(a),t);ret.sgn=(ret.num[0]==1&&!ret.num[1])?0:sgn*SGN(a);return ret;}
inline bignum& operator%=(const bignum& a){bignum_t t;div(t,num,a.num);if (num[0]==1&&!num[1])sgn=0;return *this;}
inline int operator%=(const int a){int t;div(num,ABS(a),t);memset(num,0,sizeof(bignum_t));num[0]=1;add(num,t);return t;}
inline bignum operator%(const bignum& a){bignum ret;bignum_t t;memcpy(ret.num,num,sizeof(bignum_t));div(t,ret.num,a.num);ret.sgn=(ret.num[0]==1&&!ret.num[1])?0:sgn;return ret;}
inline int operator%(const int a){bignum ret;int t;memcpy(ret.num,num,sizeof(bignum_t));div(ret.num,ABS(a),t);memset(ret.num,0,sizeof(bignum_t));ret.num[0]=1;add(ret.num,t);return t;}
inline bignum& operator++(){*this+=1;return *this;}
inline bignum& operator--(){*this-=1;return *this;};
inline int operator>(const bignum& a){return sgn>0?(a.sgn>0?comp(num,a.num)>0:1):(sgn<0?(a.sgn<0?comp(num,a.num)<0:0):a.sgn<0);}
inline int operator>(const int a){return sgn>0?(a>0?comp(num,a)>0:1):(sgn<0?(a<0?comp(num,-a)<0:0):a<0);}
inline int operator>=(const bignum& a){return sgn>0?(a.sgn>0?comp(num,a.num)>=0:1):(sgn<0?(a.sgn<0?comp(num,a.num)<=0:0):a.sgn<=0);}
inline int operator>=(const int a){return sgn>0?(a>0?comp(num,a)>=0:1):(sgn<0?(a<0?comp(num,-a)<=0:0):a<=0);}
inline int operator<(const bignum& a){return sgn<0?(a.sgn<0?comp(num,a.num)>0:1):(sgn>0?(a.sgn>0?comp(num,a.num)<0:0):a.sgn>0);}
inline int operator<(const int a){return sgn<0?(a<0?comp(num,-a)>0:1):(sgn>0?(a>0?comp(num,a)<0:0):a>0);}
inline int operator<=(const bignum& a){return sgn<0?(a.sgn<0?comp(num,a.num)>=0:1):(sgn>0?(a.sgn>0?comp(num,a.num)<=0:0):a.sgn>=0);}
inline int operator<=(const int a){return sgn<0?(a<0?comp(num,-a)>=0:1):(sgn>0?(a>0?comp(num,a)<=0:0):a>=0);}
inline int operator==(const bignum& a){return (sgn==a.sgn)?!comp(num,a.num):0;}
inline int operator==(const int a){return (sgn*a>=0)?!comp(num,ABS(a)):0;}
inline int operator!=(const bignum& a){return (sgn==a.sgn)?comp(num,a.num):1;}
inline int operator!=(const int a){return (sgn*a>=0)?comp(num,ABS(a)):1;}
inline int operator[](const int a){return digit(num,a);}
friend inline istream& operator>>(istream& is,bignum& a){read(a.num,a.sgn,is);return is;}
friend inline ostream& operator<<(ostream& os,const bignum& a){if(a.sgn<0)os<<'-';write(a.num,os);return os;}
friend inline bignum sqrt(const bignum& a){bignum ret;bignum_t t;memcpy(t,a.num,sizeof(bignum_t));sqrt(ret.num,t);ret.sgn=ret.num[0]!=1||ret.num[1];return ret;}
friend inline bignum sqrt(const bignum& a,bignum& b){bignum ret;memcpy(b.num,a.num,sizeof(bignum_t));sqrt(ret.num,b.num);ret.sgn=ret.num[0]!=1||ret.num[1];b.sgn=b.num[0]!=1||ret.num[1];return ret;}
inline int length(){return ::length(num);}
inline int zeronum(){return ::zeronum(num);}
inline bignum C(const int m,const int n){combination(num,m,n);sgn=1;return *this;}
inline bignum P(const int m,const int n){permutation(num,m,n);sgn=1;return *this;}
};
bignum q,P;
int main()
{
int t;
scanf("%d",&t);
while(t--)
{
cin>>q>>P;
if(q<3)
puts("0");
else
cout<<((q-1)*(q-2)/2)%P<<endl;
}
return 0;
}
当然,会Java大数类的小伙伴们也可以用Java来写,这样的话在现场赛遇到大数题目倒是有一些优势
import java.math.BigInteger;
import java.util.Scanner;
public class Main{
public static void main(String[] args)
{
Scanner sc = new Scanner(System.in);
int t = sc.nextInt();
for(int i=1;i<=t;i++){
BigInteger q,p;
q = sc.nextBigInteger();
p = sc.nextBigInteger();
BigInteger ans = (q.subtract(new BigInteger("1")).multiply(q.subtract(new BigInteger("2")))).divide(new BigInteger("2"));
ans = ans.mod(p);
System.out.println(ans);
}
}
}
菜鸟成长记