数据结构与算法之----图
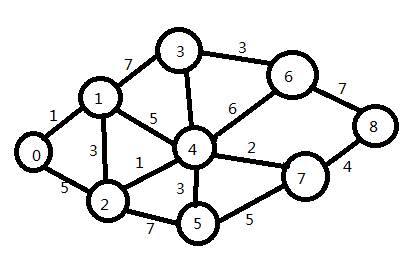
1、图的初始化
#include "stdafx.h"
#include<iostream>
using namespace std;
const int INF=65535;
struct Graph
{
int *vex;
int **arc;
int numEdges,numVexes;
};
void CreateGraph(Graph &G)
{
cout<<"请输入定点数和边数"<<endl;
cin>>G.numVexes>>G.numEdges;
G.vex=new int[G.numVexes];//为指向数组的指针
G.arc=new int*[G.numVexes];//为指针数组
for(int i=0;i<G.numVexes;i++)
G.arc[i]=new int[G.numVexes];
cout<<"请输入顶点值"<<endl;
for(int i=0;i<G.numVexes;i++)//初始化顶点
cin>>G.vex[i];
cout<<'\n';
for(int i=0;i<(G.numVexes);i++)//初始化边集数组
{ for(int j=0;j<(G.numVexes);j++)
{
if(i==j)
G.arc[i][j]=0;
else
G.arc[i][j]=INF;
}
}
cout<<"请输入边的下标v1,v2权值w"<<endl;;
int m=0,n=0,w=0;
for(int a=0;a<(G.numEdges);a++)//注意这里的G.numEdges必须()起来,否则会出问题
{
cin>>m>>n>>w;
G.arc[m][n]=w;
G.arc[n][m]=w;
}
}
int _tmain(int argc, _TCHAR* argv[])
{
Graph G;
CreateGraph(G);
for(int i=0;i<G.numVexes;i++)
cout<<G.vex[i];
cout<<'\n';
for(int i=0;i<G.numVexes;i++)
{
for(int j=0;j<G.numVexes;j++)
cout<<G.arc[i][j]<<' ';
cout<<'\n';
}
delete G.vex;
delete G.arc;
return 0;
}
注意两点:
(1)这里的顶点数组和邻接矩阵均为指针,而邻接矩阵为指向数组的指针,一定要注意其初始化方式
(2)a<G.numVexes可能会出问题,所以记得打上()
2、图的遍历
2.1 深度优先遍历
void DFS(Graph &G,int i)
{
cout<<G.vex[i]<<endl;
G.visited[i]=true;
for(int j=0;j<G.numVexes;j++)
{
if(G.arc[i][j]!=INF && (!G.visited[j]))
DFS(G,j);
}
}
void DFSTraverse(Graph &G)
{
G.visited=new int[G.numVexes];
for(int i=0;i<G.numVexes;i++)
G.visited[i]=false;
for(int i=0;i<G.numVexes;i++)
{
if(!G.visited[i])
DFS(G,i);
}
}
思想:
(1)对于每一个点,都要打印它,以及和它有连接的,且没有访问过的点。
(2)这样就用到递归,函数由两部分组成,一个是打印本节点,另外的任务是访问和它有关的节点
(3)递归主体,如果满足条件,那么就让它去执行下一个相连节点
(3)函数部分,一定要做的是先打印。
2.2 广度优先遍历
void BFSTraverse(Graph &G)
{
G.visited=new int[G.numVexes];
for(int i=0;i<(G.numVexes);i++)
G.visited[i]=false;
queue<int> Q;//这才是默认使用queue的方式,和vector的使用是一样的
for(int i=0;i<G.numVexes;i++)
{
if(!G.visited[i])
{
cout<<G.vex[i]<<endl;//此处保证就算没有连接 也可以打印出来
G.visited[i]=true;
Q.push(i);
while(Q.size())//递归都可以拆解成while循环来搞定,这个方法好,利用队列
{
i=Q.front();
Q.pop();
for(int j=0;j<G.numVexes;j++)
{
if(G.arc[i][j]<INF && (!G.visited[j]))
{
cout<<G.vex[j]<<endl;
G.visited[j]=true;
Q.push(j);
}
}
}
}
}
}
思想:
(1)将堆栈转化成队列来实现
(2)从理论上来讲,递归形成了堆栈,队列就可以不用做递归,真是太巧妙了。
(3)果然是这样的,以后要尝试用队列+while循环来解决所有递归的问题。
3、最小生成树
3.1 Prim算法
<pre name="code" class="cpp">void MiniSpan_Prim(Graph &G)
{
int k=0;
int *lowcost=new int[G.numVexes];
int *adjvex=new int[G.numVexes];
for(int i=0;i<G.numVexes;i++)
lowcost[i]=INF;//lowcost初始化
for(int i=1;i<G.numVexes;i++)//找出与顶点0相邻的顶点,并置lowcost
{
if(G.arc[0][i]<INF)
lowcost[i]=G.arc[0][i];
}
lowcost[0]=0;
for(int a=1;a<G.numVexes;a++)//找的次数
{
int min=INF;
for(int j=1;j<G.numVexes;j++)//找locost中最小的,标记下标
{
if(lowcost[j]!=0 && lowcost[j]<min)
{
min=lowcost[j];
k=j;
}
}
lowcost[k]=0;//说明该点已经找过
cout<<adjvex[k]<<" "<<k<<endl;
for(int i=1;i<G.numVexes;i++)//从这一点触发,增加有权值的新点,需要和原来locost比较
{
if(lowcost[i]!=0 && G.arc[k][i]<locost[i])//此处为修改
{
lowcost[i]=G.arc[k][i];
adjvex[i]=k;//说明前一个点为k,这样就组成了一条边
}
}
}
//打印操作
delete []lowcost;
}
思想:
(1)找到和0相邻的点,有一批lowcost值
(2)找出这批lowcost值中最小值对应的点。标记为已经找过,并打印
(3)找这个点相邻的点,加入到lowcost中,回到步骤2
(4)特点就是不断刷lowcost的值,省去了queue
4.1 克鲁斯卡尔算法(kruskal算法)
<pre name="code" class="cpp">#include "stdafx.h"
#include<iostream>
using namespace std;
const int INF=65535;
struct Edge
{
int begin;
int end;
int weight;
};
struct Graph
{
int *vex;
Edge *edges;
int numEdges,numVexes;
};
void CreateGraph(Graph &G)
{
cout<<"请输入顶点数和边数"<<endl;
cin>>G.numVexes>>G.numEdges;
G.vex=new int[G.numVexes];//为指向数组的指针
G.edges=new Edge[G.numEdges];
cout<<"请从小到大输入边"<<endl;
for(int i=0;i<G.numEdges;i++)
{
cin>>G.edges[i].begin>>G.edges[i].end>>G.edges[i].weight;
}
}
int find(int *parent,int f)
{
while(parent[f]>0)
f=parent[f];
return f;
}
void MiniSpaceTree_Kruskal(Graph &G)
{
int m,n;
int *parent=new int[G.numEdges]();
for(int i=0;i<G.numEdges;i++)
{
n=find(parent,G.edges[i].begin);
m=find(parent,G.edges[i].end);
if(m!=n)
{
parent[n]=m;//此处为修改后的
cout<<G.edges[i].begin<<" "<<G.edges[i].end<<" "<<G.edges[i].weight<<'\n';
}
}
delete []parent;//注意数组的释放
}
int _tmain(int argc, _TCHAR* argv[])
{
Graph G;
CreateGraph(G);
MiniSpaceTree_Kruskal(G);
delete []G.vex;
delete []G.edges;
return 0;
}
输出:
请输入定点数和边数
4 5
请从小到大输入边
0 1 1
2 3 1
1 2 2
1 3 2
0 2 3
4 5
请从小到大输入边
0 1 1
2 3 1
1 2 2
1 3 2
0 2 3
0 1 1
2 3 1
1 2 2
Press any key to continue
思想:
(1)顶点输入序号必须是要按照从小到大输入,小的在前面
(2)边必须按照由小到大输入,这样才能是最小生成树
(3)不断加入稍微长的,由小端标记可以达到的大端。 如果已经标记,那么大端标记为小端,这样就能够从联通的一点找到另外一点。
(4)若加入的边,不构成回路,那么记下这条边。
(5)其中find函数这种找法很不错。
5、最短路径算法
5.1 Dijkstra算法
<pre name="code" class="cpp"><pre name="code" class="cpp">#include<iostream>
using namespace std;
const int INF=65535;
struct Graph
{
int *vex;
int **arc;
int numEdges,numVexes;
};
void CreateGraph(Graph &G)
{
}
void ShortestPath_Dijkstra(Graph G,int v0,int *shortvalue,int *adjvex)
{
bool *visited=new bool[G.numVexes];
for(int i=0;i<G.numVexes;i++)
visited[i]=false;
visited[v0]=true;
shortvalue[v0]=0;
for(int i=0;i<G.numVexes;i++)
{
if(G.arc[v0][i]!=INF)
{
shortvalue[i]=G.arc[v0][i];
adjvex[i]=v0;
}
}
for(int i=1;i<G.numVexes;i++)//找当前最近的点
{
int min=INF;
int k=0;
for(int j=0;j<G.numVexes;j++)
{
if(!visited[j]&&shortvalue[j]<min)
{
min=shortvalue[j];
k=j;
}
}
for(int j=0;j<G.numVexes;j++)//对相邻的点最短距离,进行更新
{
if(!visited[j]&&min+G.arc[k][j]<shortvalue[j])
{
shortvalue[j]=min+G.arc[k][j];
adjvex[j]=k;//标记其前一个点为k
}
}
}
delete []visited;
}
思想:
(1)对刚开始的点置为访问过,更新和它相邻的点的距离。
(2)每一次都要找出一个最近且没有找过的点,标记它并更新和它相连点的距离
(3)重复2
(4)找完之后shortvalue为各个点到它的距离,adjvex为要到这个点其前一个点的下标
5.2 弗洛伊德算法(Floyd)
其思想是:从v0,到v8可以通过不同的点来进行中转,比如说v0到v8可以通过1中转更近,而1到8则通过2更近,就这样迭代下去
有两个矩阵,一个是距离D,初始化为邻接矩阵。一个位中转矩阵P,初始化为目标的下标,如0到8刚开始只能通过8中转。
对于每一个中转点,都尝试通过它进行中转,若更近,则更新距离,且更新中转点。
第一层为k,通过每一个点进行中转
第二层为v,
第三层为w
if(D[v][w]>D[v][k]+D[k][w])
{
D[v][w]=D[v][k]+D[k][w];
P[v][w]=P[v][k];
}
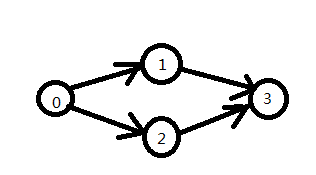
6、拓扑排序
#include<iostream>
#include<stack>
using namespace std;
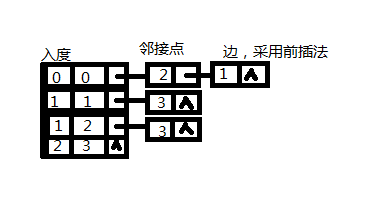
struct EdgeNode //邻接表结构
{
int adjvex;
//int weight;
EdgeNode *next;
};
struct VexNode
{
int in;
int data;
EdgeNode *fistedge;
};
struct GraphList
{
VexNode *adjlist;
int numVexes,numEdges;
};
void CreateGraphList(GraphList &G)
{
cout<<"请输入顶点和边的数目"<<endl;
cin>>G.numVexes>>G.numEdges;
G.adjlist=new VexNode[G.numVexes]();//直接初始化
cout<<"请输入顶点的的data值"<<endl;
for(int i=0;i<G.numVexes;i++)
{
cin>>G.adjlist[i].data;
}
cout<<"请输入边的出顶点,入顶点"<<endl;
for(int i=0;i<G.numEdges;i++)
{
int in,out;
cin>>in>>out;
EdgeNode *edge=new EdgeNode();
edge->adjvex=out;
edge->next=G.adjlist[in].fistedge;//利用前插法,这样就不需要遍历链表,而后插法需要先遍历到最后面才可以
G.adjlist[in].fistedge=edge;
//修改入度
G.adjlist[out].in++;
}
cout<<"显示输出效果"<<endl;
for(int i=0;i<G.numVexes;i++)
{
cout<<G.adjlist[i].in<<" ";//输出入度
EdgeNode *p=G.adjlist[i].fistedge;
while(p)
{
cout<<p->adjvex;
p=p->next;
}
cout<<'\n';
}
}
void TopLogicalSort(GraphList &G)
{
cout<<"输出拓扑排序"<<endl;
stack<int> S;
int count=0;
for(int i=0;i<G.numVexes;i++)
{
if(G.adjlist[i].in==0)
S.push(i);
}
while(S.size())
{
int a=S.top();
S.pop();
count++;
cout<<"v"<<a<<" ";
EdgeNode *p=G.adjlist[a].fistedge;
while(p)
{
if(!(--G.adjlist[p->adjvex].in))//注意是先-再使用
S.push(p->adjvex);
p=p->next;
}
}
if(count==G.numVexes)
cout<<"TopLogicalSort ok"<<endl;
else
cout<<"TopLogicalSort error"<<endl;
}
void DeleteOper(EdgeNode *edge)
{
if(!edge) return;//注意当没有出度的情况
else if(edge->next)
DeleteOper(edge->next);
else
delete edge;
}
void DeleteGraphList(GraphList &G)
{
for(int i=0;i<G.numVexes;i++)
{
DeleteOper(G.adjlist[i].fistedge);
}
}
int main()
{
GraphList G;
CreateGraphList(G);
TopLogicalSort(G);
DeleteGraphList(G);
system("pause");
}
int main()
{
cout<<"hello"<<endl;
system("pause");
}
输出:
请输入顶点和边的数目4 4请输入顶点的的data值0 1 2 3请输入边的出顶点,入顶点0 10 21 32 3显示输出效果0 211 31 32Press any key to continue
结构思想:
(1)创建邻接表需要建立3个结构,边结构,顶点结构,以及图的结构。
(2)先建立顶点数组,读入顶点值,后读入边,按照入度出度,修改顶点入度值,以及用前插法插入边,这里比后插方便太多了。
(3)删除表操作,这里还是用到递归,当然利用一个for函数对递归函数进行调用,因为这是不定次数的调用
(4)注意在递归体中注意当指针本身就为空的情况,这种情况下,需要直接返回。
(5)前插与后插的区别,前插用于链表,邻接表,而后插用于队列。
拓扑排序的作用:
拓扑排序对于一个工程的执行具有很好的指导意义,当然也可以应用于游戏开发中,一个项目中有很多个环节,一个环节需要在另外一个环节完成它才能完成,当有拓扑排序之后,就能够告诉你,先该做哪一步,再完成哪一步,按照拓扑排序出来,这样整个工程就能够执行完毕。
拓扑排序思想:
(1)压入入度为0的点
(2)不断出栈,打印顶点,并删掉出来的弧,将弧尾顶点入度减一,若入度变为0,则该顶点入栈(3)直到栈空
(4)遍历的时候一定要定义一个指针去遍历,否则会出问题,只能用while(p)或者while(p-next),当然这里用while(p)
(5)注意--在前面和在后面的问题
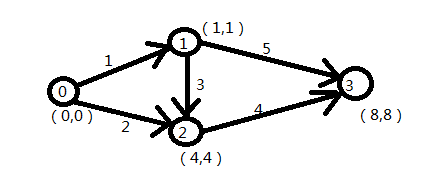
7、关键路径
解决的是工程完成需要的最短时间问题,也就是关键路径。
如果只需要求关键路径,其实在拓扑排序里面讲其标出,找出最长的路径即可。这就相当于将dikstra算法做一下小小的修改即可。
但是这里如果那样的话,对于一个项目是没有什么帮助的,另外还需要知道,每一个活动的最早开始时间和最晚开始时间。
这样就能够安排,对每一个活动进行规划和了解。
其中点为事件,()里面的为事件的最早发生时间和最晚发生时间。
要想判断每一个活动是否为关键路径,只需要用后一个事件的最晚发生时间-前一个时间的最早发生时间,判断是否相等即可。
事件的最早发生时间=前面所有活动的结束时间中的最大值,即(从前面不同事件出发+活动)中的最大值
事件的最晚发生时间=后面所有活动开始时间中的最小值,即(从后面不同事件出发-活动)中的最小值
活动的最早开始时间=事件最早发生时间
活动的最晚开始时间=活动结束后对应事件的最晚发生时间-工期
而
若两者相等,则该活动为关键路径。
另外:
一个活动的最早结束时间=最早开始时间+工期
一个活动的最晚结束时间=最晚开始时间+工期
void TopLogicalSortIn(GraphList &G,int *etv,stack<int> &S_I)
{
cout<<"输出拓扑排序"<<endl;
stack<int> S;
int count=0;
for(int i=0;i<G.numVexes;i++)
{
if(G.adjlist[i].in==0)
S.push(i);
}
while(S.size())
{
int a=S.top();
S.pop();
S_I.push(a);//事件入栈
count++;
cout<<"v"<<a<<" ";
EdgeNode *p=G.adjlist[a].fistedge;
while(p)
{
if(!(--G.adjlist[p->adjvex].in))//
S.push(p->adjvex);
if((etv[a]+p->weight)>etv[p->adjvex])
etv[p->adjvex]=etv[a]+p->weight;
p=p->next;
}
}
if(count==G.numVexes)
cout<<"TopLogicalSort ok"<<endl;
else
cout<<"TopLogicalSort error"<<endl;
}
void CriticalPath(GraphList &G)
{
int *etv=new int[G.numVexes]();
stack<int> S_I;
TopLogicalSortIn(G,etv,S_I);
cout<<endl;
for(int i=0;i<G.numVexes;i++)
cout<<etv[i]<<" ";
//求ltv
int *ltv=new int[G.numVexes];
for(int i=0;i<G.numVexes;i++)//初始化
{
ltv[i]=etv[G.numVexes-1];
}
while(S_I.size())
{
int a=S_I.top();
S_I.pop();
EdgeNode *p;
p=G.adjlist[a].fistedge;
while(p)
{
int b=p->adjvex;
int weight=p->weight;
if(ltv[b]-weight < ltv[a])
ltv[a]=ltv[b]-weight;
p=p->next;
}
}
cout<<endl;
for(int i=0;i<G.numVexes;i++)
cout<<ltv[i]<<" ";
cout<<"关键路径是"<<endl;
for(int i=0;i<G.numVexes;i++)//直接可以从开始去遍历了,不用从后面开始遍历
{
EdgeNode *p=G.adjlist[i].fistedge;
while(p)
{
int b=p->adjvex;
int weight=p->weight;
if(etv[i]==(ltv[b]-weight))
cout<<"("<<i<<","<<b<<")"<<weight<<" ";
p=p->next;
}
}
delete etv;
delete ltv;
}
思想:
(1)利用拓扑排序将可行的顺序排好S_I(堆栈),并求出事件最早发生时间etv(求最大值)
(2)将所有事件的最晚发生时间初始化为整个项目发成的最早时间(etv(v-1))。
(2)利用排好的反向顺序来读取事件,刚好从最后一个事件开始
(3)利用事件活动指向的下一个事件来确定当前事件的ltv(求最小值)
(4)遍历每一条边判断是否为关键路径(终点ltv-weight ==起点etv??)