剑指Offer面试题25(Java版):二叉树中和为某一值的路径
题目:输入一颗二叉树和一个整数,打印出二叉树中结点值的和为输入整数的所有路径。从树的根节点开始往下一直到叶结点所经过的所有的结点形成一条路径。
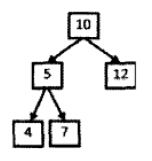
如下图,输入二叉树和整数22,则打印出两条路径,第一条路径包含结点10,12,第二条路径包含的结点为10,5,7.
一般的数据结构和算法的教材都没有介绍树的路径,因此对大多数应聘者而言,这是一个新概念,也就很难一下子想出完整的解题思路。这个时候我们可以试着从一两个具体的例子入手,找到规律。
以图中的二叉树为例分析,由于路径是从根节点出发到叶结点,也就是说路径是以根节点为起始点,因此i我们首先需要遍历根节点。在树的前序、中序、后序三种遍历方式中,只有前序遍历是首先访问根节点的。
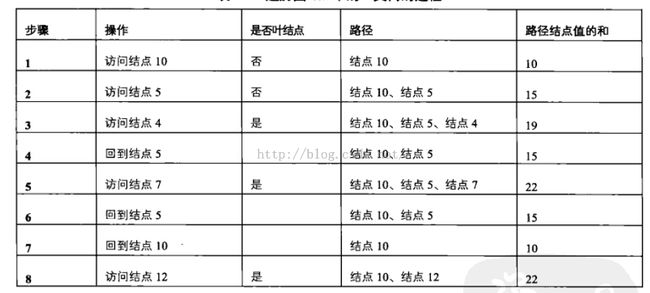
按照前序遍历的顺序遍历途中的二叉树,在访问结点10之后,就会访问结点5.从二叉树结点的定义可以看出,在本题的二叉树结点中没有指向父节点的指针,访问到结点5的时候,我们是不知道前面经过了哪些结点的,除非我们把经过的路径上的结点都保存起来。每访问到一个结点的时候,我们都把当前的结点添加到路径中去。到达结点5时,路径中包含两个结点,他们的值分别是10和5.接下来遍历到结点4,我们把这个结点也添加到路径中,这个时候已经到达了叶结点,但路径上三个结点的值之和为19.这个和不等于输入的值22,因此不符合要求的路径。
我们接着要遍历其他的结点。在遍历下一个节点之前,先要从结点4回到结点5,再去遍历结点5的右子节点7.值得注意的是,回到结点5的时候,由于结点4已经不在前往结点7的路径上了,我们需要把结点4从路径中删除。接下来访问到结点7的时候,再把结点添加到路径中。此时路径中三个结点10,5,7之和刚好是22,是一条符合要求的路径。
我们最后要遍历的结点是12.在遍历这个结点之前,需要先经过结点5回到结点10.同样,每一次当从子节点回到父节点的时候,我们都需要在路径上删除子节点。最后从结点10到达结点12的时候,路径上的两个结点的值之和也是22,因此这也是一条符合条件的路径。
总结过程如下:
分析完前面的具体的例子之后,我们就找到了一些规律。当用前序遍历的方式访问到某一节点时,我们把该结点添加到路径上,并累加该结点的值。如果该结点为叶结点并且路径中结点值的和刚好为输入的整数,则当前的路径符合要求,我们把它打印出来。如果当前的结点不是叶结点,则继续访问它的子节点。当前结点访问结束后,递归函数将自动回到它的父节点。因此我们在函数退出之前要在路径上删除当前结点并减去当前结点的值,以确保返回父节点时路径刚好是从根节点到父节点的路径。我们不难看出保存路径的数据结构实际上是一个栈,因此路径要与递归调用状态一致,而递归调用的本质上是一个压栈和出栈的过程。
用Java代码实现:
/**
* 输入一颗二叉树和一个整数,打印出二叉树中结点值的和为输入整数的所有路径。从树的根节点开始往下一直到叶结点所经过的结点形成一条路径。
*/
package swordForOffer;
import java.util.Stack;
import utils.BinaryTreeNode;
/**
* @author JInShuangQi
*
* 2015年8月5日
*/
public class E25PathInTree {
public void findPath(BinaryTreeNode root,int k){
if(root == null)
return;
Stack<Integer> stack = new Stack<Integer>();
findPath(root,k,stack);
}
public void findPath(BinaryTreeNode root,int k,Stack<Integer> path){
if(root == null)
return;
if(root.leftNode == null && root.rightNode == null){
if(root.value == k){
System.out.println("路径开始");
for(int i :path)
System.out.print(i+",");
System.out.print(root.value);
}
}
else{
path.push(root.value);
findPath(root.leftNode,k-root.value,path);
findPath(root.rightNode,k-root.value,path);
path.pop();
}
}
public static void main(String[] args){
BinaryTreeNode root1 = new BinaryTreeNode();
BinaryTreeNode node1 = new BinaryTreeNode();
BinaryTreeNode node2 = new BinaryTreeNode();
BinaryTreeNode node3 = new BinaryTreeNode();
BinaryTreeNode node4 = new BinaryTreeNode();
BinaryTreeNode node5 = new BinaryTreeNode();
BinaryTreeNode node6 = new BinaryTreeNode();
root1.leftNode = node1;
root1.rightNode = node2;
node1.leftNode = node3;
node1.rightNode = node4;
node4.leftNode = node5;
node4.rightNode = node6;
root1.value = 8;
node1.value = 8;
node2.value = 7;
node3.value = 9;
node4.value = 2;
node5.value = 4;
node6.value = 7;
E25PathInTree test = new E25PathInTree();
test.findPath(root1, 25);
}
}