Android防360水波进度
今天使用自定义view实现类似于360的水波进度提示的功能,效果如下:

实现原理
实现该效果主要用到了使用path绘制正弦波,以及xfermode知识点。可以首先绘制一个实心圆,然后设置xfermode为SRC_ATOP。
path快速学习
我们先来简单看一下path的基本用法,path可以绘制任何我们想要的图形。
mPath = new Path();
mPath.lineTo(100,100);
canvas.drawPath(mPath, mPaint);
上面通过lineTo方法画了一条线,注意这里我没有设置起始点,默认为该view的左上角,注意,是该view的左上角,而不是屏幕的左上角,这里是因为我们的view宽和高都是match_parent。
mPath = new Path();
mPath.moveTo(50,50);
mPath.lineTo(100,100);
canvas.drawPath(mPath, mPaint);
可以看到此时通过moveTo方法将起始点设置到(50,50)。
mPath = new Path();
mPath.moveTo(50,50);
mPath.arcTo(new RectF(50, 50, 300, 450), 0, 180,false);
canvas.drawPath(mPath, mPaint);
这里使用arcTo方法在矩形内切一个圆弧,当然如果该矩形是一个正方形,那就是圆了,这里我的其实角度是0度,终止角度是180,第四个参数表示是否强制将起始点移动到绘制圆弧的起始点,这么说可能不是很好理解,我们将第四个参数更改为true,效果如下:

可以看到此时绘制椭圆时候的起始点就是其起始点。
mPath = new Path();
mPath.moveTo(200,200);
mPath.lineTo(300,300);
mPath.lineTo(300,100);
mPath.lineTo(200,200);
canvas.drawPath(mPath, mPaint);
这里根据给定的三个点,绘制了一个三角形,最后的mPath.lineTo(200,200);主要是首位相接,保证最后一个点和第一个点连接,其实不必这么麻烦,可以使用Path提供的close()方法,保证线条闭合。
mPath = new Path();
mPath.moveTo(200,200);
mPath.lineTo(300,300);
mPath.lineTo(300,100);
mPath.close();
canvas.drawPath(mPath, mPaint);此时效果和上面是相同的。
另外path还提供了一系列addXX方法,用来在一个path中绘制多个图形。如下:
int width = getWidth();
int height = getHeight();
mPath = new Path();
int radius = Math.min(width, height) / 3;
mPath.addCircle(width / 2, height / 2,radius , Direction.CCW);
mPath.addRoundRect(new RectF(width / 2 - radius / 2 , height / 2 - radius / 2, width / 2 + radius / 2,height / 2 + radius / 2 ),
20.0f,20.0f,Path.Direction.CCW);
mPath.addOval(new RectF(width / 2 - radius / 3, height / 2 - radius / 3, width / 2 + radius / 3,height / 2 + radius / 3),Path.Direction.CCW);
canvas.drawPath(mPath, mPaint);
可以看到,这里我连续给path中add了三个图形,当然也可以通过”mPath.addPath(src)”方法,将另一个path描绘的图形,添加到当前的path中。
绘制贝塞尔曲线:
我们可以使用path提供的quadTo(x1, y1, x2, y2)方法来绘制任何形状的曲线。
x1, y1表示控制点的坐标
x2, y2表示终点的坐标
mPath = new Path();
mPath.moveTo(100,300);
mPath.quadTo(150, 200, 200,300);
canvas.drawPath(mPath, mPaint);
canvas.drawPoint(100,300,mPointPaint);
canvas.drawPoint(150, 200,mPointPaint);
canvas.drawPoint(200,300,mPointPaint);此时效果如下:

可以看到这样就绘制了我们半个周期的正弦曲线,使用两个quadTo方法绘制一个完整的正弦曲线:
mPath = new Path();
mPath.moveTo(100,300);
mPath.quadTo(150, 200, 200,300);
mPath.quadTo(250, 400, 300, 300);
canvas.drawPath(mPath, mPaint);
canvas.drawPoint(100,300,mPointPaint);
canvas.drawPoint(150, 200,mPointPaint);
canvas.drawPoint(200,300,mPointPaint);
canvas.drawPoint(250, 400,mPointPaint);
canvas.drawPoint(300, 300,mPointPaint);
一个完整的正弦已经绘制完成,但是这样绘制正弦曲线还不把人累死?什么时候调用quadTo方法才是个头呢??还好android为我们提供了另外一个方法,cubicTo(x1, y1, x2, y2, x3, y3),用来绘制三阶贝塞尔曲线,这个方法就可以绘制一个完整的正弦声明周期啦。
x1, y1 表示第一个控制点的坐标
x2, y2 表示第二个控制点的坐标
x3, y3 表示终点的坐标
因此,上面的代码就可以简化如下:
mPath.cubicTo(150, 200, 250, 400,300, 300);
canvas.drawPath(mPath, mPaint);其实到这里还有一个问题,那就是如果需要绘制很多个正弦连在一起cubicTo方法也是相当的不方便,因为我们需要不断的计算控制点的坐标,不怕,android中的Path还为我们提供了一些列rxxx的方法,比如rLineTo(dx, dy)方法,其实该方法和lineTo(dx, dy)的作用是一样的,唯一不同的地方在于,rLineTo(dx, dy)方法会将上一个点的坐标当成起始坐标而已,看下面的栗子:
mPath = new Path();
mPath.moveTo(100,100);
mPath.lineTo(200,200);
canvas.drawPath(mPath, mPaint);
这里起始点坐标(100,100),划线的终点坐标(200,200)。
mPath = new Path();
mPath.moveTo(100,100);
mPath.rLineTo(200,200);
canvas.drawPath(mPath, mPaint);
可以看到这里rLineTo方法将上一个点的坐标当成其实坐标(0,0)点来计算
水波进度实现
有了上面Path绘制曲线的基础以后,下面带大家一步一步实现水波进度的效果。
绘制连续的正弦曲线
由于rQuadTo方法是会将上一个坐标点当成起始坐标(0,0)点,也就是说其使用的是相对坐标,那么我们可以多次调用rQuadTo方法来绘制连续的正弦曲线,而不用计算那些烦人的控制点坐标。
mPath.reset();
mPath.moveTo(100,100);
for (int i = 0; i < 3; i++) {
mPath.rQuadTo(30, 40, 60, 0);
mPath.rQuadTo(30, -40, 60, 0);
}
canvas.drawPath(mPath, mPaint);这里我绘制了三条正弦曲线,原理如下图:
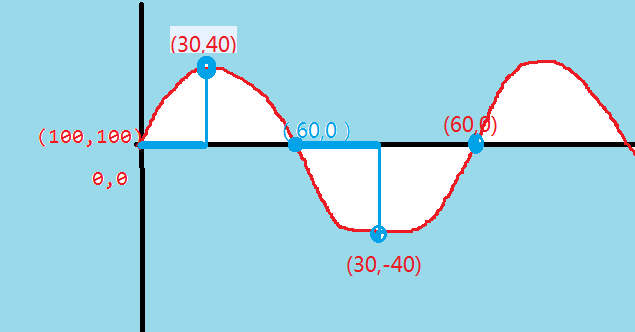
可以看到,这里的rQuadTo使用的是相对坐标,即将上一个点的坐标作为起始点(0,0),所以我们才不用计算控制点的坐标。
让曲线动起来
下面我们每次更改正弦曲线起始点的x坐标,并且不断重绘,来使当前正弦曲线动起来。
new Thread(new Runnable() {
@Override
public void run() {
while (true) {
//移动绘制正弦曲线的起始点
if (mStartX < 80) {
mStartX += 5;
} else {
mStartX = 0;
}
//改变当前震动的幅度
mSinMax += 5;
if (mShouldUp) {
if (mSinMax > 20) {
mShouldUp = false;
}
} else {
mSinMax -= 5;
if (mSinMax < -20) {
mShouldUp = true;
}
}
try {
Thread.sleep(200);
} catch (InterruptedException e) {
e.printStackTrace();
}
postInvalidate();
}
}
}).start();
@Override
protected void onDraw(Canvas canvas) {
super.onDraw(canvas);
mPath.reset();
mPath.moveTo(mStartX,100);
for (int i = 0; i < 4; i++) {
mPath.rQuadTo(20, mSinMax, 40, 0);
mPath.rQuadTo(20, -mSinMax, 40, 0);
}
canvas.drawPath(mPath, mPaint);
}在这里,我通过线程不断改变当前曲线的其实绘制坐标,以及当前震动的幅度。此时效果如下:
一张图看懂原理
请看下面的图:

是不是有点恍然大悟的赶脚,对,只要在中间绘制一个圆,在加之以xfermode的使用,就完成了我们最开始的效果。
这里整个图形的绘制代码如下:
mPath.moveTo(450,100); //矩形右上角
mPath.lineTo(450, 300); //矩形右下角
mPath.lineTo(mStartX,300); //矩形左下角
mPath.lineTo(mStartX, 100); //矩形左上角
for (int i = 0; i < 5; i++) {
mPath.rQuadTo(20, mSinMax, 40, 0);
mPath.rQuadTo(20, -mSinMax, 40, 0);
}
canvas.drawPath(mPath, mPaint);可以看到这里实际上就是绘制了一个矩形,并且让该矩形的x轴随着当前正弦曲线需要的起始点移动,并且绘制5个正弦曲线。
可以看到这里我们需要使用SRC_ATOP或者DST_ATOP这两种模式中的一个。
具体实现
使用到的属性
private Paint mPaint; //绘制波形
private Paint mCirclePaint; //绘制圆形
private Path mPath; //记录波形的路径
private int width; //自定义view的宽度
private int height; //自定义view的高度
private int mCirclePaintRadius; //绘制圆形的半径
private int mStepSize; //绘制波形的完整周期的宽度
private int mMoveStartX; //绘制波形的初始位置,相当于震动的频率
private int mSinMax; //绘制波形的振幅
private int count = 3; //需要绘制完整波形的个数,个数越多,波形的周期越小
private Canvas mCircleCanvas;
private Bitmap mDest;
private int mCurrentProgress; //当前的进度
private boolean shouldChange; //用于控制正弦线的上升和下降
private Paint mTextPaint;
private Rect mBound;初始化方法
private void init() {
//设置绘制水波画笔的属性
mPaint=new Paint(Paint.ANTI_ALIAS_FLAG);
mPaint.setColor(Color.parseColor("#99FF99"));
mPaint.setAntiAlias(true);
mPaint.setStrokeWidth(5);
mPaint.setStyle(Paint.Style.FILL);
PorterDuffXfermode mode = new PorterDuffXfermode(PorterDuff.Mode.SRC_ATOP);
mPaint.setXfermode(mode);
mPath = new Path();
//设置绘制背景圆的画笔属性
mCirclePaint = new Paint(Paint.ANTI_ALIAS_FLAG);
mCirclePaint.setStyle(Paint.Style.FILL);
mCirclePaint.setColor(Color.parseColor("#CCCCFF"));
mCirclePaint.setStrokeWidth(5);
//绘制文字的画笔
mTextPaint = new Paint(Paint.ANTI_ALIAS_FLAG);
mTextPaint.setTextSize(30);
mTextPaint.setColor(Color.parseColor("#3399FF"));
mBound = new Rect();
}可以看到我在初始化方法中,初始化了三个画笔,以及path,rect等。
计算初始值
在onMeasure方法中根据当前view的大小计算圆形,以及正弦曲线的周期等。
@Override
protected void onMeasure(int widthMeasureSpec, int heightMeasureSpec) {
super.onMeasure(widthMeasureSpec, heightMeasureSpec);
width = getMeasuredWidth();
height = getMeasuredHeight();
mCirclePaintRadius = Math.min(width,height) / 3;
//计算mStepSize(1/4周期)的大小
mStepSize = (int) (Math.min(width,height) / 3.0f * 2) / (count * 4);
mDest = Bitmap.createBitmap(width, height, Config.ARGB_8888);
mCircleCanvas = new Canvas(mDest);
}重写onDraw方法
下面重写onDraw方法来绘制当前的进度图形。
@Override
protected void onDraw(Canvas canvas) {
super.onDraw(canvas);
//线绘制一个实心圆
mCircleCanvas.drawCircle(width / 2, height / 2, mCirclePaintRadius, mCirclePaint);
//每次绘制记得调用reset()方法,否则当前绘制会和上次的绘制重叠
mPath.reset();
//下面的moveTo,lineTo,lineTo,lineTo主要是让当前正弦线的首位相接
mPath.moveTo(width / 2 + mCirclePaintRadius, height / 2
+ mCirclePaintRadius
- (mCurrentProgress * (mCirclePaintRadius * 2 / 100.f)));
mPath.lineTo(width / 2 + mCirclePaintRadius, height / 2
+ mCirclePaintRadius);
mPath.lineTo(mMoveStartX, height / 2 + mCirclePaintRadius);
mPath.lineTo(mMoveStartX, height / 2 + mCirclePaintRadius
- (mCurrentProgress * (mCirclePaintRadius * 2 / 100.f)));
for (int i = 0; i < (count + 1); i++) {
mPath.rQuadTo(mStepSize,mSinMax, mStepSize * 2, 0);
mPath.rQuadTo(mStepSize,-mSinMax,mStepSize * 2,0);
}
mCircleCanvas.drawPath(mPath, mPaint);
canvas.drawBitmap(mDest,0,0,null);
//准备绘制当前进度
String text = mCurrentProgress+"%";
mTextPaint.getTextBounds(text, 0, text.length(), mBound);
canvas.drawText(text, width / 2 - mBound.width() / 2 , height / 2 + mBound.height() / 2 , mTextPaint);
}改变初始位置和当前振幅
new Thread(new Runnable() {
@Override
public void run() {
while (mCurrentProgress < 100) {
mMoveStartX += Math.random() * 15; //正弦线的初始位置
//当当前初始位置 > 半个周期的时候,重新从头开始绘制
if (mMoveStartX >= mStepSize) {
mMoveStartX = 0;
}
if (shouldChange) { //正弦线上升部分,mSinMax是振幅
mSinMax++;
if (mSinMax == 0) {
mSinMax = 5;
}
if (mSinMax > 18) {
shouldChange = false;
}
} else { //正弦线下降部分
mSinMax--;
if (mSinMax == 0) {
mSinMax = -5;
}
if (mSinMax <= -18) {
shouldChange = true;
mSinMax = 3;
// mSinMax = 0;
}
}
//改变当前进度
mCurrentProgress += Math.round(Math.random() * 4);
if (mCurrentProgress >= 100) {
mCurrentProgress = 100;
mSinMax = 0; //当进度是100%的时候将振幅重置为0,这样就会填充整个圆形
}
try {
Thread.sleep(300);
} catch (InterruptedException e) {
e.printStackTrace();
}
//重新绘制当前view
postInvalidate();
}
}
}).start();这里开启一个线程,不断的重新改变当前正弦曲线绘制的起始点坐标,并且不断重绘。上面的说明比较详细,这里我就不啰嗦了。
虽然看起来实现了一点效果,不过我个人觉得这样还是很不科学,比如由于该view还有很大的一部分我们是看不到的,但是仍然很占位置,这样就很不好,哪位大神有更好的思路也可以给予指导。
今天就到这儿啦。源码下载

