计算机图形学（二）输出图元_4_并行画线算法

并行画线算法

本来在word中是有右下数的，一编辑在csdn中编辑就没有了。

                          

       上面讨论过的线段生成算法顺序地确定像素位置。而利用并行计算机，则可通过将计算分割到可用的多个处理器中来得到线段的像素位置。分割问题的一种解决方法是将现有的顺序算法放到多个处理器上。我们也可以寻找其他处理办法，从而使像素位置能以并行方式有效地计算。在设计并行算法中，重要的是要考虑平衡可用处理器间的处理负载。
       给定np个处理器，我们可以通过把线段分割成np个子段，并在每个子段中同时生成线段而建立起并行的Bresenham画线算法。对于斜率为0 < m < 1.0且左端点坐标位置为(xo,yo)的线段，我们沿正x方向对线段进行分割。相邻分段的起始x位置间的距离可计算为

其中，△x是线段的水平宽度，分段水平宽度△xp的值利用整数除法来计算。将分段和处理器从0,1, 2直到np- 1编号，可以计算出第k分段的起始的、坐标为

        例如△x = 15，并且具有np = 4个处理器，那么分段的水平宽度是4，各分段的初始x值为xo 、xo +4、xo +8 , xo + 12。对于这种分段策略，有些情况下最后(最右边)的子段会比其他段小。此外，假如线段的端点不是整数，舍入误差将导致沿线的长度产生宽度不同的分段。为了将Bresenham算法用于各分段，需要有每个分段的y坐标初始值和决策参数的初始值。分段y方向的变化△y，可从线段斜率m和分段宽度△xp计算得出:

那么，第k分段的起始y坐标为

第k分段起始处Bresenham算法的初始决策参数可从等式(3.14)中得到

       然后，各处理器利用该分段的初始决策参数值和起始坐标(xk,yk)，计算指定的分段上的像素位置。我们也可以通过替换m = △y/△x和重新安排有关项，将yk和pk起始值计算中的浮点运算简化为整数运算。在y方向对线段进行分段并计算分段的起始x值，可以将并行Bresenham算法拓展到斜率大于1.0的线段。对于负斜率，则可以在一个方向递增坐标值，而在另一方向上递减。
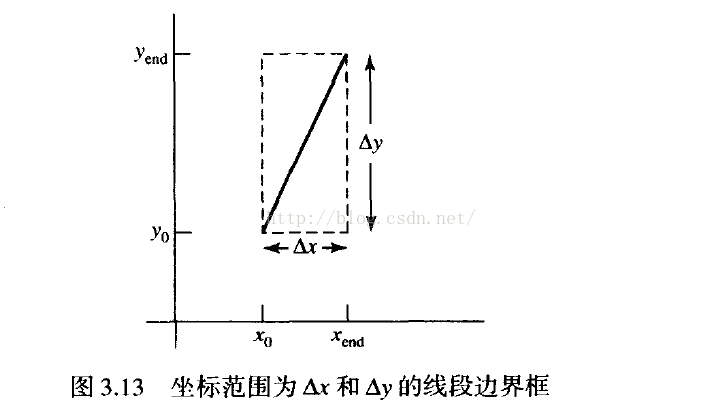
       建立光栅系统并行算法的另一种方法是，为每个处理器分配一组屏幕像素。只要具有足够数量的处理器，就可以将每个处理器分配给某个屏幕区域内的一个像素。这种方法可以通过为一个处理器分配线段坐标范围之内的一个像素并计算像素距线段的距离而移植成线段显示的方法。在线段的包围盒中的像素数目为△x.△y, (参见图3.13 )。在图3.13中，从线段到坐标(x, y)处像素的垂直距离d，可以利用下列算式得到:

其中

并且

一旦估算出线段的常量A, B和C，那么每个处理器只需完成两次乘法和两次加法来计算像素距离d。如果d小于指定的线段粗细参数，那么就绘制一个像素。

    除了把屏幕分割成单个像素，我们也可以按线段的斜率为每个处理器分配一条扫描线或一列像素。然后，每个处理器计算线段与分配给该处理器的水平行或垂直列的交点。对于斜率|m| < 1.0的线段，每个处理器将简单地按给定的x值从直线方程中求解y。对于斜率值大于1.0的线段，处理器则根据给定的扫描线y值，从直线方程中求解x。尽管这种直接方法在顺序算法机器中的计算速很慢，但通过使用多处理器能十分有效地完成这一算法。