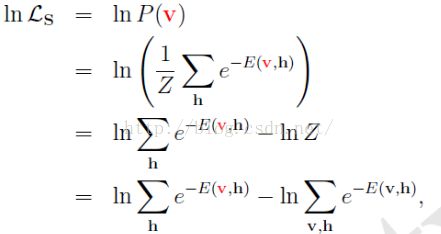deep learning tutorial(四)Restricted Boltzmann Machines (RBM)

只是看了很多东西自己的一些整理，方便复习

本文部分公式内容摘自http://blog.csdn.net/itplus/article/details/19169027 作者: peghoty 

产生式模型：用来估计联合概率P(x,y), 因此可以根据联合概率来生成样本，如HMM
判别式模型：用来估计条件概率P(y|x),因为没有x的知识，无法生成样本，只能判断分类，如SVM,CRF,MEM(最大熵)

关于生成模型和判别模型的详细解释http://blog.csdn.net/zouxy09/article/details/8195017

1.基于能量的模型（EBM）

其中规范化因子Z被称为配分函数：

关于能量函数和能量模型的一点解释:

       能量函数：受统计力学中能量泛函的启发，是描述整个系统状态的一种测度，系统越有序或者概率分布越集中，系统的能量越小；反之，系统越无须或者概率分布越趋于均匀分布，则系统能量越大。能量函数的最小值，对于系统的最稳定状态。

       能量模型：能量模型把系统的每个状态与一个能量（由能量函数给出）对应，能量模型定义p(x)为处于该状态下的概率分布

定义其损失函数为负的对数似然函数

（1）

很多情况下，样本x的分布是未知的，因此需要引人一些隐含的参数在增加模型的表达能力

（2）

对参数求导得

（3）

     其中前面一项叫做positive phase,后面一项叫做negtive phase.positive项增加了训练样本(training data)的概率，negtive项增加了由模型产生的样本的概率

     进一步求导得（v代表vk）:

（4）

上式中。

       但是我们现在还不知道它符合哪个分布

受限玻尔兹曼机 (RBM)

玻尔兹曼机是一种特殊的对数线性形式的马尔可夫随机场，即能量方程是线性的

（5）

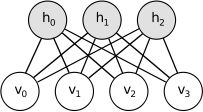
如图，RBM是一个二分图，由可视节点和个隐藏节点构成，层间相连接（可视节点和隐藏节点链接），层内无连接（层内的节点是相互独立的），就是这个可视节点的状态只受隐藏节点的影响，由能量函数的定义我们可以看出，每个状态是由独立的可视层节点，独立的隐藏节点，以及可视节点和隐藏节点之间的连接构成的

由于，层内相互独立，我们可以给出这样连乘的形式

RBMs with binary 

当节点的值为{0,1}时，有

具体推到过程http://blog.csdn.net/itplus/article/details/19168989

回到公式（4），由于

（6）

故只需要讨论的分布

最终得到

（7）

详细推导过程请看这里http://blog.csdn.net/itplus/article/details/19207371

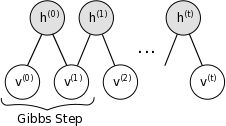
可是v是未知的，我们并不知道v的概率分布函数，h是我们加入的隐含参数，因此我们需要估计v

Sampling in an RBM

p(x)的样本可以通过马氏链收敛定理获得，利用gibbs采样在马氏链上做状态转移上作状态转移。

Gibbs采样：得到一个指定的分布，我们首先在N个随机变量上进行N次采样，采样的过程不断模拟马尔可夫过程，不断进行状态转移。设系统为,我们每次从条件分布中进行采样，Si={S1,S2,...

S(i-1),S(i+1),...Sn}

具体推导看这里

http://www.52nlp.cn/lda-math-mcmc-%E5%92%8C-gibbs-sampling1

http://www.52nlp.cn/lda-math-mcmc-%E5%92%8C-gibbs-sampling2

对RBMs来说，S由可视节点和隐藏节点组成。由于可视节点之间，隐藏节点之间分别是条件独立的，因此我们可以在给定隐藏节点的值后，一次性算出所有可视节点的值，反之亦然：

其中代表第n步所有的隐藏节点，然后计算出，代表以这个概率被随机赋值为0或者1

下图可以表述这个转移过程

当时，就会趋近于真实的，gibbs采样算法如下

对比散度算法 (CD-k)

       对比散度算法 使用了两个技巧来加速采样的过程

        1.因为我们的目标是让RBM拟合训练样本的分布，所以可以考虑让MCMC的状态以训练样本为起点，那么只需要很少次数的状态转移就可以快速收敛

         2.不需要等到状态收敛，只执行k步Gibbs采样，在实际应用中，k取1就可以得到比较好的学习效果

RBM算法还有许多变形和改进，用到了再更