POJ 2528 Mayor's posters（离散化+线段树）

Mayor's posters

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 55517		Accepted: 16098

Description

The citizens of Bytetown, AB, could not stand that the candidates in the mayoral election campaign have been placing their electoral posters at all places at their whim. The city council has finally decided to build an electoral wall for placing the posters and introduce the following rules: 

• Every candidate can place exactly one poster on the wall. 
  
• All posters are of the same height equal to the height of the wall; the width of a poster can be any integer number of bytes (byte is the unit of length in Bytetown). 
  
• The wall is divided into segments and the width of each segment is one byte. 
  
• Each poster must completely cover a contiguous number of wall segments.

They have built a wall 10000000 bytes long (such that there is enough place for all candidates). When the electoral campaign was restarted, the candidates were placing their posters on the wall and their posters differed widely in width. Moreover, the candidates started placing their posters on wall segments already occupied by other posters. Everyone in Bytetown was curious whose posters will be visible (entirely or in part) on the last day before elections. 
Your task is to find the number of visible posters when all the posters are placed given the information about posters' size, their place and order of placement on the electoral wall. 

Input

The first line of input contains a number c giving the number of cases that follow. The first line of data for a single case contains number 1 <= n <= 10000. The subsequent n lines describe the posters in the order in which they were placed. The i-th line among the n lines contains two integer numbers l _i and ri which are the number of the wall segment occupied by the left end and the right end of the i-th poster, respectively. We know that for each 1 <= i <= n, 1 <= l _i <= ri <= 10000000. After the i-th poster is placed, it entirely covers all wall segments numbered l _i, l _i+1 ,... , ri.

Output

For each input data set print the number of visible posters after all the posters are placed. 

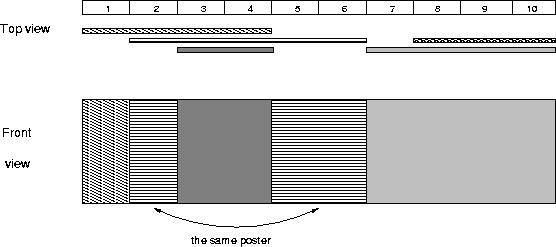
The picture below illustrates the case of the sample input. 

Sample Input

1
5
1 4
2 6
8 10
3 4
7 10

Sample Output

4

 用到线段树，因为最多有10^6，建那么大的树肯定会爆空间和时间，所以想到要离散化，将每条线段的两端，就是海报的两头分开考虑，所有的端点放在一起非递减排序，

去掉相同的，计算出有n个不同的点，编号从1到n，——这是离散化过程。然后建二叉树。更新的时候先二分查找那条线段两端的点

的编号，然后在那棵建好的树上更新，遇到一样的节点就覆盖，如果线段在那个节点的子节点上，而且这个节点又被其他线段覆盖

过，那么就要更新它的子节点，他自己改成不被覆盖的。最后计算结果那里要用个辅助数组，从根节点开始找被覆盖的节点，分别

将不同的值放在数组里，最后看有几个结果就是几个。

#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>

using namespace std;
const int maxn = 10010;
struct node
{
    int l, r;
} Poster[maxn];
int Section[maxn*2];
int Hash[maxn*1000];
struct Tree
{
    int l, r;
    bool flag;
} ans[maxn*10];

void Build(int l, int r, int rt)
{
    ans[rt].l = l, ans[rt].r = r;
    ans[rt].flag = false;
    if(l == r)  return;
    int mid = (l + r) >> 1;
    Build(l, mid, rt<<1);
    Build(mid+1, r, rt<<1|1);
}

bool Judge(int l, int r, int rt)
{
    if(ans[rt].flag) return false;
    if(l == ans[rt].l && r == ans[rt].r){
        ans[rt].flag = true;
        return true;
    }
    bool Flag;
    int mid = (ans[rt].l + ans[rt].r) >> 1;
    if(r <= mid) Flag = Judge(l, r, rt<<1);
    else if(l > mid) Flag = Judge(l, r, rt<<1|1);
    else{
        bool flag1 = Judge(l, mid, rt<<1);
        bool flag2 = Judge(mid+1, r, rt<<1|1);
        Flag = (flag1 || flag2);
    }
    if(ans[rt<<1].flag && ans[rt<<1|1].flag) ans[rt].flag = true;
    return Flag;
}

int main()
{
    int T, n;
    scanf("%d",&T);
    while(T-- && scanf("%d",&n)){
        int Count = 0;
        for(int i=0; i<n; i++){
            scanf("%d%d",&Poster[i].l, &Poster[i].r);
            Section[Count++] = Poster[i].l, Section[Count++] = Poster[i].r;
        }
        sort(Section, Section+Count);
        Count = unique(Section, Section+Count) - Section;
        for(int i=0; i<Count; i++)
            Hash[Section[i]] = i;
        Build(0, Count-1, 1);
        int ant = 0;
        for(int i=n-1; i>=0; i--)
            if(Judge(Hash[Poster[i].l], Hash[Poster[i].r], 1))
                ant++;
        printf("%d\n",ant);
    }
    return 0;
}