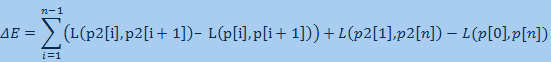AI中的几种搜索算法---SA搜索算法

AI中的几种搜索算法---SA搜索算法

引言

SA （Simulated Annealing）搜索算法,就如它的名字，是模仿了退火的处理过程。在提到TSP问题的时候,经常会使用该算法进行解决。

一、SA搜索算法的基本介绍

1.SA算法流程

该算法的流程如下

1.     首先便是初始化工作，设置初始温度（temperature）,获得一个随机的解决方案，并将其设置为当前解决方案（cur_sol）。

2.     如果温度大于0，处理cur_sol（perturb处理，比如随机调换方案中步骤执行顺序等），得到新方案（new_sol）；如果温度小于0，结束算法。

3.     比较当前方案和新方案的消耗（deltaE = cost(new_sol) – cost(cur_sol)）。

4.     如果deltaE小于0则表明新方案比当前方案优秀，将新方案设置为当前方案，降温，则继续执行步骤2。

5.     根据公式p = exp(-detaE/T)。计算p将其与以小于1的正随机数比较。如果p大于随机数，正将新方案设置为当前方案，降温继续执行步骤2；如果p小于随机数，则降温直接执行步骤2。

这个流程可以简单的理解：不断获取新方案，和当前比较，如果优于当前方案，取新方案为当前方案；如果劣于当前方案，则给予它一个机会成为当前方案，这个机会的概率取决于当前的温度和它与当前方案之间的差距。

二、TSP问题

这里举TSP问题，这个在SA搜索中最常用的例子。

1.   TSP问题介绍

TSP问题即旅行商问题：一个旅行商A被分配到一个任务，公司要求A去几个城市进行公司业务拓展，所以A就会拿出地图制定一个合理的路线。其中路线的要求便是消耗最小，并且能够从某一个城市出发，并且最后返回该城市时，已经访问过了所有城市。

2.   TSP问题分析

首先我们需要联系一下SA算法，将几个TSP中的概念对应到SA中。路线便是我们要搜索的解决方案（solution），路线所经历的长度便是SA中的消耗，这样问题就简单了。

至于perturb处理，便是调换路线中两个城市的顺序比如

Cur_sol: A->B->C->D->E->A

经过perturb处理后得到new_sol

New_sol:A->B->D->C->E->A

我们可以随机调换两个城市的访问顺序。

接下来便是p = exp(-detaE/T)。联系TSP问题这个公式中

p和p2都为路线，p为当前路线，p2为新路线。p[i]表示路线中的第i个城市，L(x,y)表示城市x和城市y之间的距离。

3.   TSP问题核心代码

我写了一个程序演示TSP问题的解决，感兴趣的读者可以去 TSP问题项目下载

 int tsp_sa(City * cities,intnCities,int ** path)
 {
     if(nCities< 2)
         return-1;
     doubletemperature = 100.0;
     *path = new int[nCities];
     int *newpath = new int[nCities];
     GetRandomPath(nCities,*path);

     longcurdistance = CaculateDistance(cities,nCities,*path);
     while(temperature> 1.0)
     {
         memcpy(newpath,*path,nCities*sizeof(int));
         PerturbPath(nCities,newpath);
         longnewdistance = CaculateDistance(cities,nCities,newpath);
         longdeltE = newdistance - curdistance;
         if(deltE< 0)
         {
             memcpy(*path,newpath,sizeof(int) *nCities);
             curdistance = newdistance;
         }
         else
         {
             doublep = exp(-1 * deltE / temperature) ;
             doublerandp = ((double)rand()/(double)RAND_MAX);
             if(p> randp)//给新方案一个机会成为当前方案
             {
                 memcpy(*path,newpath,sizeof(int) *nCities);
                 curdistance = newdistance;
             }
         }
         temperature -= 0.01;
     }
     delete[]newpath;
     return 1;
 }

说明其中City是一个自定义的结构体，保存了城市的位置。PerturbPath函数则是随机调换路线中两个城市的访问顺序。

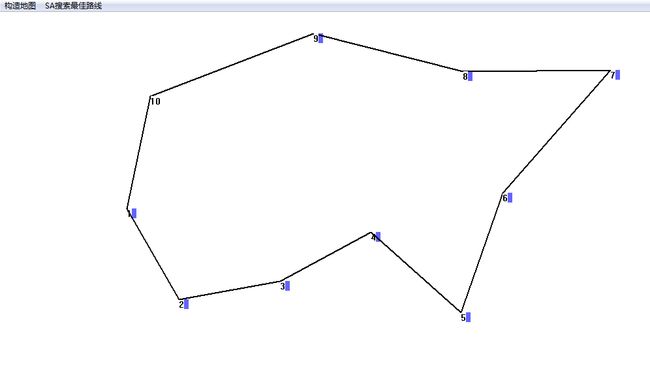
4.   TSP程序截图

三、总结

SA算法，随着温度越来越低，获得的方案也是越来越稳定，因为温度的降低，是的采纳非优方案的概率越来越低。至于为什么还要给非优方案一个机会，是因为要避免局部最优（Local Optimum）。