排序算法系列之八大排序算法性能比较-从实验结果分析

shu*于2015/8/25修改:

关于各大排序算法的基本思想以及具体分析请参考作者前面几篇文章，这篇主要对各大排序算法进行一下总结和对比。

依据串行（list）的大小（n）。一般而言，好的表现是O(n log n)，且坏的行为是O(n2)。对于一个排序理想的表现是O(n)。仅使用一个抽象关键比较运算的排序算法总平均上总是至少需要O(n log n)。

	平均情况	最好情况	最坏情况
归并排序	O(nlogn)	O(nlogn)	O(nlogn)
基数排序	O(n)	O(n)	O(n)
快速排序	O(nlogn)	O(nlogn)	O(n2)
希尔排序	O(n1.5)	O(n)	O(n1.5)
插入排序	O(n2)	O(n)	O(n2)
选择排序	O(n2)	O(n2)	O(n2)
堆排序	O(nlogn)	O(nlogn)	O(nlogn)
冒泡排序	O(n2)	O(n)	O(n2)

回顾各大排序算法的实现代码：

// SORT.cpp : 定义控制台应用程序的入口点。
//

#include "stdafx.h"
#include <iostream>
#include <time.h>
#include <vector>
using namespace std;

template<class T>
void BubbleSort(T *x, const int N)
{
	for(int k= N-1; k>0 ;k--)
	{
		for(int i=0; i<k; i++)
		{
			if(x[i] > x[i+1])
			{
				T temp = x[i];
				x[i] = x[i+1];
				x[i+1] = temp;
			}
		}
	}
}

</pre><pre name="code" class="cpp"><pre name="code" class="cpp">//改进版BubbleSort
template<class T>
void BubbleSort(T *x, const int N)
{
	bool flag = false;
	for(int k= N-1; k>0 ;k--)
	{
		for(int i=0; i<k; i++)
		{
			if(x[i] > x[i+1])
			{
				T temp = x[i];
				x[i] = x[i+1];
				x[i+1] = temp;
				flag = true;
			}
		}
		if(!flag)
			return;
	}
}

<pre name="code" class="cpp">template<class T>
void SelectSort(T *x, const int N)//不稳定
{
	for(int i =0; i < N; i++)
	{
		int minindex = i;
		for(int j = i; j < N; j++ )
		{
			if(x[minindex] > x[j])
			{
				minindex = j;
			}
		}
		if(minindex != i)
		{
			T temp = x[i];
			x[i] = x[minindex];
			x[minindex] = temp;
		}
	}
}


template<class T>
void InsertSort(T *x,const int N)
{
	for(int i = 1; i<N; i++)
	{
		T temp = x[i];
		int j;
		for(j = i-1; j>=0 && temp<x[j] ;j--)
		{
			x[j+1] = x[j];
		}
		x[j+1] = temp;
	}
}


template<class T>
void QuickSort(T *x, int low, int high)
{
	if(high-low<=0)
		return;

	T split = x[low];
	int	splitIndex = low;
	int i = low, j = high;
	while(i < j)
	{
		while(i < j && split <=x[j])
		{
			j--;	
		}

		if(i < j)
		{
			x[i] = x[j];
			x[j] = split;
			splitIndex = j;
			i++;
		}

		while(i < j && x[i]<=split)
		{
			i++;
		}

		if(i < j)
		{
			x[j] = x[i];
			x[i] = split;
			splitIndex = i;
		}
	}

	QuickSort(x,low,splitIndex-1);
	QuickSort(x,splitIndex+1,high);
}


template<class T>
void ShellSort(T *x, const int N)
{
	int d = N/2;//增量步长
	for(d;d >=1;d/=2)
	{
	//	cout<<d<<endl;
		for(int i = 0;i<d; i++)
		{
			for(int j = i; j <N-d ; j+=d)//部分插入排序
			{
				for(int m = j+d; m-d>=0 && x[m]< x[m-d]; m-=d)
				{
					T temp = x[m];
					x[m] = x[m-d];
					x[m-d] = temp;
				}
			}
		}
	}
}

template<class T>
void  HeapAdjust(T *H, int start ,int end)//已知H[start~end]中除了start之外均满足堆的定义
//本函数进行调整，使H[start~end]成为一个大顶堆
{

	T temp = H[start];
    for(int i = 2*start + 1; i<=end; i*=2)
    {
        //因为假设根结点的序号为0而不是1，所以i结点左孩子和右孩子分别为2i+1和2i+2
        if(i<end && H[i]<H[i+1])//左右孩子的比较
        {
            ++i;//i为较大的记录的下标
        }

        if(temp > H[i])//左右孩子中获胜者与父亲的比较
        {
            break;
        }
        //将孩子结点上位，则以孩子结点的位置进行下一轮的筛选
        H[start]= H[i];
        start = i;
    }

    H[start]= temp; //插入最开始不和谐的元素
}


template<class T>
void HeapSort(T *H, const int n)
{
	int N = n-1;
	//建立最大堆
	for(int i = N/2; i>=0; --i)//认为叶子节点是有序的，则只需从叶子节点的父节点开始调整
	{
		HeapAdjust(H,i,N);
	}
	for(int i = N; i>=1;--i)
	{
		T temp = H[0];
		H[0] = H[i] ;
		H[i] = temp;
		HeapAdjust(H,0,i-1);
	}
}

template<class T>
void MergeArray(T *x,int left, int mid, int right)
{
	T *temp = new int[right - left + 1];
	int i = left;
	int j = mid+1;
	int m =mid;
	int n = right;
	int k = 0;
	while( i <= m && j <= n)
	{
		if(x[i] < x[j])
			temp[k++] = x[i++];
		else
			temp[k++] = x[j++];
	}
	while(i <= m)
		temp[k++] = x[i++];
	while(j <= n)
		temp[k++] = x[j++];

	for(int i = 0; i < right - left + 1; i++)
	 x[i + left] = temp[i];
}


template<class T>
void MergeSort(T *x, int left , int right)
{
	if(left < right)
	{
		int mid = (left + right)/2;
		MergeSort(x, left, mid);
		MergeSort(x, mid+1, right);
		MergeArray(x, left, mid, right);//再将二个有序数列合并  
	}
}

#define MAXBIT 3
template<class T>
void RadixSort(T *x, const int N)
{
	vector<T>Bucket[10];
	for(int b = 1; b <= MAXBIT; b++)
	{
		int basicbit = pow(10 , b);
		for(int i = 0; i < N; i++)
		{
			int index = (x[i] % basicbit) / (basicbit/10) ;
			Bucket[index].push_back(x[i]);
		}

		int n = 0;
		for(int j =0 ; j <= 9 ; j++)
		{
			for(int m = 0;  m < Bucket[j].size(); m++)
			{
				x[n++] = Bucket[j][m]; 
			}
			Bucket[j].clear();
		}
	}
}

定义了两个产生随机整数和随机浮点数的函数

void randomInt(int *x,const int N)
{
	srand((unsigned)time(NULL));
	for(int i = 0; i < N; i++)
	{
		x[i] = rand()%500; 
	}
}

void randomFloat(float *x,const int N)
{
	srand((unsigned)time(NULL));
	for(int i = 0; i < N; i++)
	{
		x[i] = float(rand()%500)/499.0*500.0; 
	}
}

以及一个打印函数

template<class T>
void print(T *x, const int N)
{
	int i;
	for(i=0; i<N; i++)
	{
		cout<<x[i]<<" ";
		if((i+1)%10==0)
			cout<<endl;
	}
	cout<<endl;
}

主函数中对各种排序函数进行调用，并输出排序时间与排序结果，当N较大时省略排序结果

int main(int argc,char **argv)
{
	int N = 1000;
	int *intA = new int[N];
	randomInt(intA , N);
	print(intA , N);
	
	int *A1 = new int[N],*A2 = new int[N],*A3 = new int[N],*A4= new int[N],*A5= new int[N],*A6= new int[N],*A7= new int[N],*A8= new int[N];
	for(int i = 0; i< N;i++)
	{
		A1[i] = A2[i] = A3[i] = A4[i] = A5[i] = A6[i] = A7[i] = A8[i] = intA[i];
	}

	clock_t s1,f1,s2,f2,s3,f3,s4,f4,s5,f5,s6,f6,s7,f7,s8,f8;

	s1 = clock();
	BubbleSort(A1 , N);
	f1 = clock();
	float t1 = (float)((f1 - s1)*1000.0/CLOCKS_PER_SEC);
	cout<<"BubbleSort: "<<t1<<" ms"<<endl;
	print(A1 , N);

	s2 = clock();
	SelectSort(A2 , N);
	f2 = clock();
	float t2 = (float)((f2 - s2)*1000.0/CLOCKS_PER_SEC);
	cout<<"SelectSort: "<<t2<<" ms"<<endl;
	print(A2 , N);

	s3 = clock();
	InsertSort(A3 , N);
	f3 = clock();
	float t3 = (float)((f3 - s3)*1000.0/CLOCKS_PER_SEC);
	cout<<"InsertSort: "<<t3<<" ms"<<endl;
	print(A3 , N);

	s4 = clock();
	QuickSort(A4 ,0,N-1);
	f4 = clock();
	float t4 = (float)((f4 - s4)*1000.0/CLOCKS_PER_SEC);
	cout<<"QuickSort: "<<t4<<" ms"<<endl;
	print(A4 , N);

	s5 = clock();
	ShellSort(A5, N);
	f5 = clock();
	float t5 = (float)((f5 - s5)*1000.0/CLOCKS_PER_SEC);
	cout<<"ShellSort: "<<t5<<" ms"<<endl;
	print(A5 , N);

	s6 = clock();
	HeapSort(A6 , N);
	f6 = clock();
	float t6 = (float)((f6 - s6)*1000.0/CLOCKS_PER_SEC);
	cout<<"HeapSort: "<<t6<<" ms"<<endl;
	print(A6 , N);

	s7 = clock();
	MergeSort(A7 , 0 , N-1);
	f7 = clock();
	float t7 = (float)((f7 - s7)*1000.0/CLOCKS_PER_SEC);
	cout<<"MergeSort: "<<t7<<" ms"<<endl;
	print(A7 , N);

	s8 = clock();
	RadixSort(A8 , N);
	f8 = clock();
	float t8 = (float)((f8 - s8)*1000.0/CLOCKS_PER_SEC);
	cout<<"RadixSort: "<<t8<<" ms"<<endl;
	print(A8 , N);

	//float *floatA = new float[N];
	//randomFloat(floatA , N);
	//print(floatA , N);
	//BubbleSort(floatA , N);
	//SelectSort(floatA , N);
	//InsertSort(floatA , N);
	//QuickSort(floatA ,0,N-1);
	//ShellSort(floatA , N);
	//print(floatA , N);

	return 0;
}

（1）验证结果正确性：

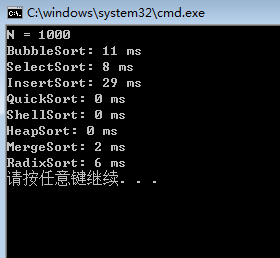
（2）N=1000时，时间比较：

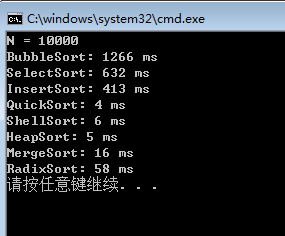
（3）N =10000时，时间比较：

（4）N = 50000,

发现一个很好的排序归纳网页：http://blog.chinaunix.net/uid-25324849-id-2182899.html