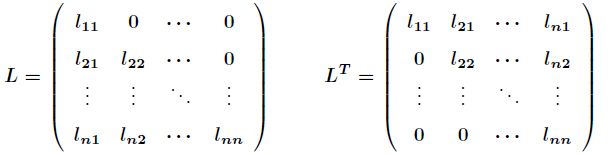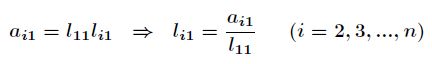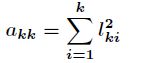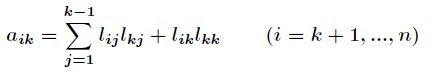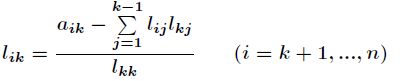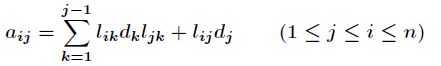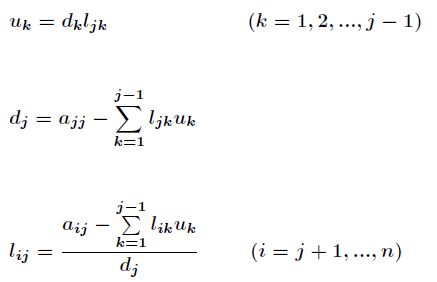Cholesky分解法

Cholesky分解法又叫平方根法，是求解对称正定线性方程组最常用的方法之一。对于一般矩阵，为了消除LU分

解的局限性和误差的过分积累，采用了选主元的方法，但对于对称正定矩阵而言，选主元是不必要的。

 

定理：若对称正定，则存在一个对角元为正数的下三角矩阵，使得成立。

 

假设现在要求解线性方程组，其中为对称正定矩阵，那么可通过下面步骤求解

 

（1）求的Cholesky分解，得到

（2）求解，得到

（3）求解，得到

 

现在的关键问题是对进行Cholesky分解。假设

 

       

 

通过比较两边的关系，首先由，再由

 

       

 

这样便得到了矩阵的第一列元素，假定已经算出了的前列元素，通过

 

       

 

可以得到

 

       

 

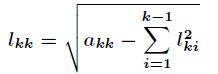
进一步再由

 

                 

 

最终得到

 

       

 

这样便通过的前列求出了第列，一直递推下去即可求出，这种方法称为平方根法。

 

代码：

#include <iostream>
#include <string.h>
#include <stdio.h>
#include <vector>
#include <math.h>

using namespace std;
const int N = 1005;
typedef double Type;

Type A[N][N], L[N][N];

/** 分解A得到A = L * L^T */
void Cholesky(Type A[][N], Type L[][N], int n)
{
    for(int k = 0; k < n; k++)
    {
        Type sum = 0;
        for(int i = 0; i < k; i++)
            sum += L[k][i] * L[k][i];
        sum = A[k][k] - sum;
        L[k][k] = sqrt(sum > 0 ? sum : 0);
        for(int i = k + 1; i < n; i++)
        {
            sum = 0;
            for(int j = 0; j < k; j++)
                sum += L[i][j] * L[k][j];
            L[i][k] = (A[i][k] - sum) / L[k][k];
        }
        for(int j = 0; j < k; j++)
            L[j][k] = 0;
    }
}

/** 回带过程 */
vector<Type> Solve(Type L[][N], vector<Type> X, int n)
{
    /** LY = B  => Y */
    for(int k = 0; k < n; k++)
    {
        for(int i = 0; i < k; i++)
            X[k] -= X[i] * L[k][i];
        X[k] /= L[k][k];
    }
    /** L^TX = Y => X */
    for(int k = n - 1; k >= 0; k--)
    {
        for(int i = k + 1; i < n; i++)
            X[k] -= X[i] * L[i][k];
        X[k] /= L[k][k];
    }
    return X;
}

void Print(Type L[][N], const vector<Type> B, int n)
{
    for(int i = 0; i < n; i++)
    {
        for(int j = 0; j < n; j++)
            cout<<L[i][j]<<" ";
        cout<<endl;
    }
    cout<<endl;
    vector<Type> X = Solve(L, B, n);
    vector<Type>::iterator it;
    for(it = X.begin(); it != X.end(); it++)
        cout<<*it<<" ";
    cout<<endl;
}

int main()
{
    int n;
    cin>>n;
    memset(L, 0, sizeof(L));
    for(int i = 0; i < n; i++)
    {
        for(int j = 0; j < n; j++)
            cin>>A[i][j];
    }
    vector<Type> B;
    for(int i = 0; i < n; i++)
    {
        Type y;
        cin>>y;
        B.push_back(y);
    }
    Cholesky(A, L, n);
    Print(L, B, n);
    return 0;
}

/**data**
4
4 -2 4 2
-2 10 -2 -7
4 -2 8 4
2 -7 4 7
8 2 16 6
*/

用上述的方法需要进行开方，这有可能损失精度和增加运算量，为了避免开方，Cholesky分解有个改进的版本。

 

将对称正定矩阵通过分解成，其中是单位下三角矩阵，是对角均为正数的对角矩阵。把这

一分解叫做分解，是Cholesky分解的变形。对应两边的元素，很容易得到

 

          

 

由此可以确定计算和的公式如下

 

          

 

在实际计算时，是将的严格下三角元素存储在的对应位置上，而将的对角元存储在的对应的对角位置上。

类似地求解线性方程组的解步骤如下

 

（1）对矩阵进行分解得到

（2）求解，得到

（3）求解，得到

 

代码：

#include <iostream>
#include <string.h>
#include <stdio.h>
#include <vector>
#include <math.h>

using namespace std;
const int N = 1005;
typedef double Type;

Type A[N][N], L[N][N], D[N][N];

/** 分解A得到A = LDL^T */
void Cholesky(Type A[][N], Type L[][N], Type D[][N], int n)
{
    for(int k = 0; k < n; k++)
    {
        for(int i = 0; i < k; i++)
            A[k][k] -= A[i][i] * A[k][i] * A[k][i];
        for(int j = k + 1; j < n; j++)
        {
            for(int i = 0; i < k; i++)
                A[j][k] -= A[j][i] * A[i][i] * A[k][i];
            A[j][k] /= A[k][k];
        }
    }
    memset(L, 0, sizeof(L));
    memset(D, 0, sizeof(D));
    for(int i = 0; i < n; i++)
    {
        D[i][i] = A[i][i];
        L[i][i] = 1;
    }
    for(int i = 0; i < n; i++)
    {
        for(int j = 0; j < i; j++)
            L[i][j] = A[i][j];
    }
}

void Transposition(Type L[][N], int n)
{
    for(int i = 0; i < n; i++)
    {
        for(int j = 0; j < i; j++)
            swap(L[i][j], L[j][i]);
    }
}

void Multi(Type A[][N], Type B[][N], int n)
{
    Type **C = new Type*[n];
    for(int i = 0; i < n; i++)
        C[i] = new Type[n];
    for(int i = 0; i < n; i++)
    {
        for(int j = 0; j < n; j++)
        {
            C[i][j] = 0;
            for(int k = 0; k < n; k++)
                C[i][j] += A[i][k] * B[k][j];
        }
    }
    for(int i = 0; i < n; i++)
    {
        for(int j = 0; j < n; j++)
            B[i][j] = C[i][j];
    }
    for(int i = 0; i < n; i++)
    {
        delete[] C[i];
        C[i] = NULL;
    }
    delete C;
    C = NULL;
}

/** 回带过程 */
vector<Type> Solve(Type L[][N], Type D[][N], vector<Type> X, int n)
{
    /** LY = B  => Y */
    for(int k = 0; k < n; k++)
    {
        for(int i = 0; i < k; i++)
            X[k] -= X[i] * L[k][i];
        X[k] /= L[k][k];
    }
    /** DL^TX = Y => X */
    Transposition(L, n);
    Multi(D, L, n);
    for(int k = n - 1; k >= 0; k--)
    {
        for(int i = k + 1; i < n; i++)
            X[k] -= X[i] * L[k][i];
        X[k] /= L[k][k];
    }
    return X;
}

void Print(Type L[][N], Type D[][N], const vector<Type> B, int n)
{
    for(int i = 0; i < n; i++)
    {
        for(int j = 0; j < n; j++)
            cout<<L[i][j]<<" ";
        cout<<endl;
    }
    cout<<endl;
    vector<Type> X = Solve(L, D, B, n);
    vector<Type>::iterator it;
    for(it = X.begin(); it != X.end(); it++)
        cout<<*it<<" ";
    cout<<endl;
}

int main()
{
    int n;
    cin>>n;
    memset(L, 0, sizeof(L));
    for(int i = 0; i < n; i++)
    {
        for(int j = 0; j < n; j++)
            cin>>A[i][j];
    }
    vector<Type> B;
    for(int i = 0; i < n; i++)
    {
        Type y;
        cin>>y;
        B.push_back(y);
    }
    Cholesky(A, L, D, n);
    Print(L, D, B, n);
    return 0;
}

/**data**
4
4 -2 4 2
-2 10 -2 -7
4 -2 8 4
2 -7 4 7
8 2 16 6
*/

 

参考资料：http://class.htu.cn/nla/cha1/sect3.htm