I do. 【附：C++用不多于一条推博字符数的代码能作出怎样的图像？】

以上为原创主贴

以下为转帖及少量翻译。

很多C++程序员在进行的一场比赛：

用不多于一条微博的字符数的代码能作出怎样的数学图像？

http://codegolf.stackexchange.com/questions/35569/tweetable-mathematical-art

比赛用的基础代码及其来源：http://pastebin.com/uQkCQGhz

// NOTE: compile with g++ filename.cpp -std=c++11
//    also, if this doesn't work for you, try the alternate char-based version

#include <iostream>

// NOTE: compile with g++ filename.cpp -std=c++11
//    also, if this doesn't work for you, try the alternate char-based version
 
#include <iostream>
#include <cmath>
#define DIM 1024
#define DM1 (DIM-1)
#define _sq(x) ((x)*(x))                           // square
#define _cb(x) abs((x)*(x)*(x))                    // absolute value of cube
#define _cr(x) (unsigned short)(pow((x),1.0/3.0))  // cube root
 
unsigned short GR(int,int);
unsigned short BL(int,int);
 
unsigned short RD(int i,int j){
    // YOUR CODE HERE
}
unsigned short GR(int i,int j){
    // YOUR CODE HERE
}
unsigned short BL(int i,int j){
    // YOUR CODE HERE
}
 
void pixel_write(int,int);
FILE *fp;
int main(){
    fp = fopen("MathPic","wb");
    fprintf(fp, "P6\n%d %d\n1023\n", DIM, DIM);
    for(int j=0;j<DIM;j++)
        for(int i=0;i<DIM;i++)
            pixel_write(i,j);
    fclose(fp);
    return 0;
}
void pixel_write(int i, int j){
    static unsigned short color[3];
    color[0] = RD(i,j)&DM1;
    color[1] = GR(i,j)&DM1;
    color[2] = BL(i,j)&DM1;
    fwrite(color, 2, 3, fp);
}

悄悄问一声：看到有人画美国国旗，但那个难度似乎高些，画的不够完整；

我国国旗简单明快，谁能把我国的国旗给插上去？即使不参赛过去围观学习也不错

以前用LaTeX-pstricks做过一个，关键点坐标都计算好了：

http://blog.csdn.net/stereohomology/article/details/42736953

\documentclass[10pt]{article}
\usepackage{pstricks-add}
\pagestyle{empty}
\begin{document}
\psset{xunit=1.0cm,yunit=1.0cm,algebraic=true,dimen=middle,dotstyle=o,dotsize=3pt 0,linewidth=0.8pt,arrowsize=3pt 2,arrowinset=0.25}
\begin{pspicture*}(-0.46457050781696785,-0.37965822469965455)(30.294541312811983,20.492596225012818)
\pspolygon[linecolor=red,fillcolor=red,fillstyle=solid,opacity=1.0](0.,0.)(30.,0.)(30.,20.)(0.,20.)
\pspolygon[linecolor=yellow,fillcolor=yellow,fillstyle=solid,opacity=1.0](5.,17.)(4.550972023420415,15.618033988749897)(3.0978869674096927,15.618033988749895)(4.2734574719946385,14.76393202250021)(3.8244294954150537,13.381966011250105)(5.,14.236067977499788)(6.175570504584947,13.381966011250105)(5.726542528005363,14.76393202250021)(6.902113032590307,15.618033988749895)(5.449027976579585,15.618033988749897)
\pspolygon[linecolor=yellow,fillcolor=yellow,fillstyle=solid,opacity=1.0](9.21913119055697,11.624695047554425)(9.618445490913444,11.017725415257024)(9.164577971830825,10.450391016403751)(9.865235300727628,10.642597552358211)(10.264549601084108,10.03562792006081)(10.29826534445257,10.761387724437943)(10.99892267334938,10.953594260392398)(10.31910281981025,11.209931951211484)(10.352818563178719,11.935691755588616)(9.898951044096098,11.36835735673534)
\pspolygon[linecolor=yellow,fillcolor=yellow,fillstyle=solid,opacity=1.0](11.038476052359176,13.274721127897376)(11.641194023588783,12.86901792091315)(11.441597440829744,12.170429881256497)(12.013694215439054,12.618279549652073)(12.616412186668681,12.212576342667852)(12.36726946700181,12.89506586657091)(12.939366241611147,13.342915534966485)(12.213290798198107,13.31686758930872)(11.964148078531252,13.99935711321179)(11.7645514957722,13.300769073555118)
\pspolygon[linecolor=yellow,fillcolor=yellow,fillstyle=solid,opacity=1.0](11.010050506338834,15.85857864376269)(11.725839855604015,15.734040888527788)(11.828588485278617,15.014800480805578)(12.168222002235074,15.657072322910002)(12.884011351500249,15.532534567675102)(12.378127059432817,16.05401815134753)(12.717760576389267,16.69628999345197)(12.065473372560458,16.376312730632204)(11.559589080493035,16.897796314304657)(11.662337710167638,16.178555906582442)
\pspolygon[linecolor=yellow,fillcolor=yellow,fillstyle=solid,opacity=1.0](9.142507074287456,17.485504244572475)(9.850531607407726,17.648492911357117)(10.224334654204075,17.025487833363208)(10.28811483374484,17.749225447211057)(10.996139366865116,17.912214113995685)(10.327533152509602,18.196519891505766)(10.39131333205037,18.9202575053536)(9.914311786948504,18.372230525204948)(9.245705572592987,18.65653630271503)(9.619508619389325,18.033531224721116)
\end{pspicture*}
\end{document}

它的草图设计是这样的，如果直接从设计图出发也可以：

发现这个帖子的过程是这样的：

1. 先从知乎上看到一个用C++代码例子的问答，代码是转帖，但是结果相当漂亮。

http://www.zhihu.com/question/30262900/answer/48741026

2 然后根据链接找到了顾森的博客：

http://www.matrix67.com/blog/archives/6039

3. 最终发现是stackexchange上的。

http://codegolf.stackexchange.com/questions/35569/tweetable-mathematical-art

我比较喜欢的是这种：

<span style="font-size:12px;">unsigned char RD(int i,int j){
    float s=3./(j+99);
    float y=(j+sin((i*i+_sq(j-700)*5)/100./DIM)*35)*s;
    return (int((i+DIM)*s+y)%2+int((DIM*2-i)*s+y)%2)*127;
}
unsigned char GR(int i,int j){
    float s=3./(j+99);
    float y=(j+sin((i*i+_sq(j-700)*5)/100./DIM)*35)*s;
    return (int(5*((i+DIM)*s+y))%2+int(5*((DIM*2-i)*s+y))%2)*127;
}
unsigned char BL(int i,int j){
    float s=3./(j+99);
    float y=(j+sin((i*i+_sq(j-700)*5)/100./DIM)*35)*s;
    return (int(29*((i+DIM)*s+y))%2+int(29*((DIM*2-i)*s+y))%2)*127;
}</span>

unsigned char RD(int i,int j){
#define P 6.03
float s=3./(j+250),y=(j+sin((i*i+_sq(j-700)*5)/100./DIM+P)*15)*s;return (int((i+DIM)*s+y)%2+int((DIM*2-i)*s+y)%2)*127;}

unsigned char GR(int i,int j){
float s=3./(j+250);
float y=(j+sin((i*i+_sq(j-700)*5)/100./DIM+P)*15)*s;
return (int(5*((i+DIM)*s+y))%2+int(5*((DIM*2-i)*s+y))%2)*127;}

unsigned char BL(int i,int j){
float s=3./(j+250);
float y=(j+sin((i*i+_sq(j-700)*5)/100./DIM+P)*15)*s;
return (int(29*((i+DIM)*s+y))%2+int(29*((DIM*2-i)*s+y))%2)*127;}

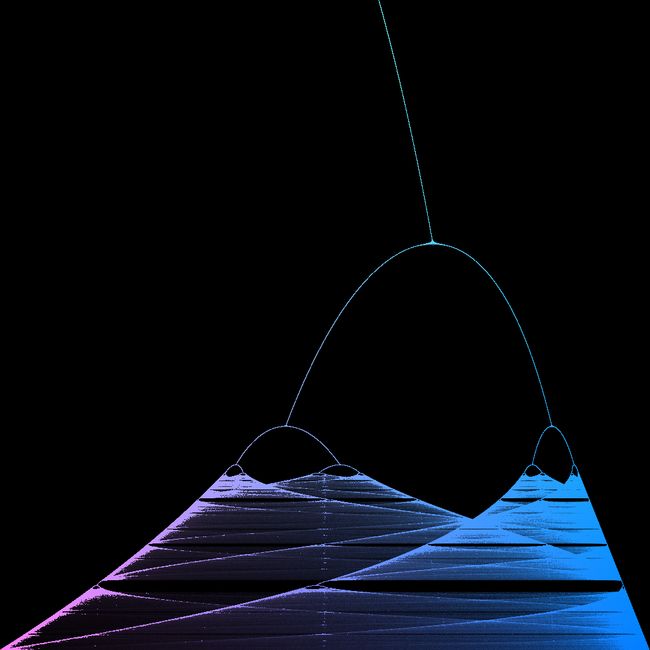
以及这种：

unsigned char RD(int i,int j){    
    #define A float a=0,b,k,r,x
    #define B int e,o
    #define C(x) x>255?255:x
    #define R return
    #define D DIM
    R BL(i,j)*(D-i)/D;
}
unsigned char GR(int i,int j){      
    #define E DM1
    #define F static float
    #define G for(
    #define H r=a*1.6/D+2.4;x=1.0001*b/D
    R BL(i,j)*(D-j/2)/D;
}
unsigned char BL(int i,int j){
    F c[D][D];if(i+j<1){A;B;G;a<D;a+=0.1){G b=0;b<D;b++){H;G k=0;k<D;k++){x=r*x*(1-x);if(k>D/2){e=a;o=(E*x);c[e][o]+=0.01;}}}}}R C(c[j][i])*i/D;
}

<span style="font-size:12px;">for(double a=0;a<DIM;a+=0.1){       // Incrementing a by 1 will miss points
    for(int b=0;b<DIM;b++){         // 1024 here is arbitrary, but convenient
        double r = a*(1.6/DIM)+2.4; // This is the r in the logistic bifurcation diagram (x axis)
        double x = 1.0001*b/DIM;    // This is x in the logistic bifurcation diagram (y axis). The 1.0001 is because nice fractions can lead to pathological behavior.
        for(int k=0;k<DIM;k++){
            x = r*x*(1-x);          // Apply the logistic map to x
            // We do this DIM/2 times without recording anything, just to get x out of unstable values
            if(k>DIM/2){
                if(c[(int)a][(int)(DM1*x)]<255){
                    c[(int)a][(int)(DM1*x)]+=0.01; // x makes a mark in c[][]
                } // In the golfed code, I just always add 0.01 here, and clip c to 255
            }
        }            
    }    
}</span>

因为绝大多数代码答案并没有特殊的针对某种平台的独特的函数或命令，

初步测试，Visual C++、GCC都可编译。

只不过有库的限制和字符数的约定，build的时候可能会出现很多warning

那些为了节约代码而定义了很多宏的，显然不是经济的风格，相当低效。不过反正只是一种代码填字游戏。