贪心算法_哈夫曼编码问题(Huffman Coding)

       哈夫曼编码问题，可以用贪心算法来解还是比较爽的啊(上一篇博客我还在想贪心算法能解的问题不多)。下面来详细讨论一下哈夫曼编码问题。

      问题描述:现有一个文本文件，其中包含的字符数据出现的次数各不相同，先要求对该文本中包含的字符进行编码，使文本占用的位数更小。

      问题分析：我们知道文件的存储都是以二进制数表示的，如：字符c可以表示为010101...之类的。因为不同的操作系统对于不同的数据类型会分配给相同的数据容器长度，如java中int型数据固定占用4个字节的存储空间。现在问题时因为各个字符出现的概率不同，那么我们就可以给出现概率高的字符分配以"短"的二进制表示数，给出现概率低的字符分配以"长"的二进制表示数。从而达到降低平均每字符占用的空间数，进而实现无损的空间压缩。

      OK，我们来论证哈夫曼编码问题的贪心选择性质。这里必须介绍一下的是，我们会使用二叉树这种数据结构来解哈夫曼问题。从根节点到叶节点经过的路径就是某个叶节点对象(这里就是字符)的编码值。那么从直觉(恩，直觉，我觉的解贪心算法的话，直觉很重要)上将讲，应该将概率低的元素放置到树的底部，将概率高的元素放置到树的顶部。代码如下:

package com.wly.algorithmbase.greedy;

import java.util.ArrayList;

/**
 * 贪心算法解哈夫曼编码问题
 * 
 * @author wly
 * 
 */
public class HuffmanCode {

	public static void main(String[] args) {

		ArrayList<HuffmanNode> list = new ArrayList<HuffmanNode>();

		list.add(new HuffmanNode(null, null, "A", 0.3f));
		list.add(new HuffmanNode(null, null, "B", 0.1f));
		list.add(new HuffmanNode(null, null, "C", 0.35f));
		list.add(new HuffmanNode(null, null, "D", 0.05f));
		list.add(new HuffmanNode(null, null, "E", 0.2f));

		print(getHuffmanCodeNode(list));
	}

	/**
	 * 得到表示当前输入节点的树结构
	 * @param list
	 * @return
	 */
	public static HuffmanNode getHuffmanCodeNode(ArrayList<HuffmanNode> list) {

		while (list.size() >= 2) {
			//1.排序元素
			srotNodeListByKey(list);

			//2.合并key值最小的两个节点(因为已经排序过了，此处就是列表的前两项)
			HuffmanNode newNode = combine2SmallestNode(list.get(0), list.get(1));
			list.remove(0);
			list.remove(0); //注意ArrayList中remove元素时的索引移动s
			list.add(0, newNode);
		}
		
		return list.get(0);
	}
	
	/**
	 * 打印某个节点的树结构，即以该节点为根节点的子树结构s
	 * @param node
	 */
	public static void print(HuffmanNode node) {
		System.out.print("| " + node.getData() + "," + node.getPercent() + " |");
		if(node.getLeftN() != null) {
			print(node.getLeftN());
		} 
		
		if(node.getRightN() != null) {
			print(node.getRightN());
		} 
	}	
	
	/**
	 * 使用冒泡排序，按key值单调递增排序
	 * 
	 * @param list
	 */
	public static void srotNodeListByKey(ArrayList<HuffmanNode> list) {
		for (int i = 0; i < list.size(); i++) {
			for (int j = i+1; j < list.size(); j++) {
				if (list.get(i).getPercent() > list.get(j).getPercent()) {
					// 交换位置
					list.add(i, list.get(j));
					list.remove(j+1);
					
					list.add(j, list.get(i + 1));
					list.remove(i + 1);
				}
			}
		}
	}


	/**
	 * 将两个子节点合成为一个父节点
	 * 
	 * @param leftNode
	 * @param rightNode
	 * @return
	 */
	private static HuffmanNode combine2SmallestNode(HuffmanNode leftNode,
			HuffmanNode rightNode) {
		HuffmanNode parentNode = new HuffmanNode(leftNode, rightNode,
				leftNode.getData() + rightNode.getData(), leftNode.getPercent()
						+ rightNode.getPercent());
		return parentNode;
	}
}

/**
 * 用于表示哈夫曼编码的二叉树的节类
 * 
 * @author wly
 * 
 */
class HuffmanNode {

	private HuffmanNode leftN; //左子节点
	private HuffmanNode rightN; //右子节点
	private String data; // 包含的数据，本程序中指的是字符
	private float percent; // 检索key值

	public HuffmanNode(HuffmanNode leftN, HuffmanNode rightN, String data,
			float key) {
		super();
		this.leftN = leftN;
		this.rightN = rightN;
		this.data = data;
		this.percent = key;
	}

	public float getPercent() {
		return percent;
	}

	public void setPercent(float percent) {
		this.percent = percent;
	}

	public HuffmanNode getLeftN() {
		return leftN;
	}

	public void setLeftN(HuffmanNode leftN) {
		this.leftN = leftN;
	}

	public HuffmanNode getRightN() {
		return rightN;
	}

	public void setRightN(HuffmanNode rightN) {
		this.rightN = rightN;
	}

	public String getData() {
		return data;
	}

	public void setData(String data) {
		this.data = data;
	}

}

      运行结果：

| DBEAC,1.0 || DBE,0.35000002 || DB,0.15 || D,0.05 || B,0.1 || E,0.2 || AC,0.65 || A,0.3 || C,0.35 |

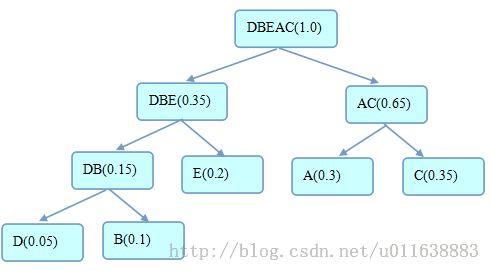
      从运行结果可以得到二叉树如下:

      即各个字符的编码分别是:D:000、D:001、E:01、A:10、C:11

      若不进行编码按相同字长编码，则至少需要3位，那么需要存储ABCDE的尺寸为:3*1=3

      编码后，存储ABCDE的尺寸为:3*0.05+3*0.1+2*0.2+2*0.3+2*0.2=1.85

      可见使用哈夫曼编码能够在一定程度上实现数据的无损压缩。

      O啦~~~

      转载请保留出处:http://blog.csdn.net/u011638883/article/details/16857309

      谢谢!!