问题描述:
The n-queens puzzle is the problem of placing n queens on an n×n chessboard such that no two queens attack each other.
Given an integer n, return all distinct solutions to the n-queens puzzle.
Each solution contains a distinct board configuration of the n-queens' placement, where 'Q' and '.' both indicate a queen and an empty space respectively.
For example,
There exist two distinct solutions to the 4-queens puzzle:
[ [".Q..", // Solution 1 "...Q", "Q...", "..Q."], ["..Q.", // Solution 2 "Q...", "...Q", ".Q.."] ]
原问题链接:https://leetcode.com/problems/n-queens/
问题分析
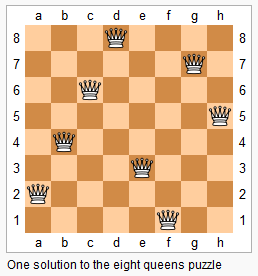
这是经典的8皇后问题的一个衍生。对于这个问题的要求来说,我们需要在给定的n行n列的 矩阵里找到n个元素,它们每个元素即不在同一行,也不在同一列,同时也不在对角线上。以下图为例:
在图中a点上,它所在的行与列,以及两个方向的对角线上的位置都不能放其他的元素。这样才算是一个合格的位置。这样,由于我们需要在每一行放置一个元素,所以这些所有n个元素必须都满足上面这个条件。
那么,现在该怎么来实现它呢?因为我们要找到所有符合条件的布局,所以一种思路就是我们从第一行起遍历这一行的每一个位置,然后递归的去下一行设置下一个元素,直到最后一行。每次我们选择可以在当前行放置的元素才能递归到下一步。
从实现的细节来看,我们可以定义一个递归的函数nQueens(List<List<String>> result, int[] positions, int cur, int n)。这里result用来保存最终的结果,在每次递归调用到最后一行的时候表示找到了一个符合条件的结果,要把结果加入到result中间,所以需要把它作为一个参数传递进来。positions这个数组用来保存在当前行之前每一步所放置元素的位置。比如说第一行元素放置的是第一列,那么positions[0] = 0,0即是这个位置的索引。每次当前位置找到合格的元素之后就将该元素的索引设置到positions[cur]这个位置。这个递归函数的一个返回条件是当cur == n的时候。n表示矩阵的行数。
另外一个,对于任意两个点所在行i, j,我们要判断它们是否构成合法的布局,可以通过判断它们两个是否在同一行(i == j), 同一列(positions[i] == positions[j])以及同一对角线(Math.abs(j - i) == Math.abs(positions[j] - positions[i]))来确定。所以经过上述的讨论,可以得到如下的代码:
public class Solution {
public List<List<String>> solveNQueens(int n) {
List<List<String>> result = new ArrayList<>();
if(n < 1) return result;
int[] positions = new int[n];
nQueens(result, positions, 0, n);
return result;
}
public void nQueens(List<List<String>> result, int[] positions, int cur, int n) {
if(cur == n) {
result.add(generatePosition(positions, n));
return;
}
for(int i = 0; i < n; i++) {
if(validPosition(i, cur, positions)) {
positions[cur] = i;
nQueens(result, positions, cur + 1, n);
}
}
}
public boolean validPosition(int i, int cur, int[] positions) {
for(int j = 0; j < cur; j++) {
if(positions[j] == i || Math.abs(j - cur) == Math.abs(i - positions[j])) return false;
}
return true;
}
public List<String> generatePosition(int[] positions, int n) {
List<String> list = new ArrayList<>();
for(int i = 0; i < positions.length; i++) {
StringBuilder sb = new StringBuilder();
for(int j = 0; j < n; j++) {
if(j == positions[i]) sb.append('Q');
else sb.append('.');
}
list.add(sb.toString());
}
return list;
}
}