福州大学第十三届程序设计竞赛_重现总结
Accept: 82 Submit: 425
Time Limit: 2000 mSec Memory Limit : 32768 KB
 Problem Description
Problem Description
在一个平面内给定n个点,任意三个点不在同一条直线上,用这些点可以构成多少个平行四边形?一个点可以同时属于多个平行四边形。
 Input
Input
多组数据(<=10),处理到EOF。
每组数据第一行一个整数n(4<=n<=500)。接下来n行每行两个整数xi,yi(0<=xi,yi<=1e9),表示每个点的坐标。
 Output
Output
每组数据输出一个整数,表示用这些点能构成多少个平行四边形。
 Sample Input
Sample Input
 Sample Output
Sample Output
思路:
因为三个点不在同一条直线上,所以我们只需要处理出任意两个点之间的x,y之差,
对x,y以x为第一关键字,y为第二关键字排序,然后判断相同的x,y总共有多少对。
Accept: 54 Submit: 268
Time Limit: 1000 mSec Memory Limit : 32768 KB
 Problem Description
Problem Description
GG学长虽然并不打炉石传说,但是由于题面需要他便学会了打炉石传说。但是传统的炉石传说对于刚入门的GG学长来说有点复杂,所以他决定自己开发一个简化版的炉石传说。
在简化版的炉石传说中:
每个随从只有生命值和攻击力,并且在你的回合下,你的每只随从在本回合下只能选择一个敌方随从进行攻击。当两个随从a,b交战时,a的生命值将减去b的攻击力,b的生命值将减去a的攻击力,(两个伤害没有先后顺序,同时结算)。如果a或b的生命值不大于0,该随从将死亡。
某一次对局中,GG学长和对手场面上均有n个随从,并且是GG学长的回合。由于GG学长是个固执的boy,他一定要在本回合杀死对方所有随从,并且保证自己的随从全部存活。他想知道能否做到。
 Input
Input
第一行为T,表示有T组数据。T<=100。
每组数据第一行为n,表示随从数量(1 <= n <= 100)
接下来一行2 * n个数字a1, b1, a2, b2, ... , an, bn (1 <= ai, bi <= 100)
表示GG学长的n个随从,ai表示随从生命,bi表示随从攻击力
接下来一行2 * n个数字c1, d1, c2, d2, ... , cn, dn (1 <= ci, di <= 100)
表示对手的n个随从,ci表示随从生命,di表示随从攻击力。
 Output
Output
每组数据,根据GG是否能完成他的目标,输出一行”Yes”或”No”。
 Sample Input
Sample Input
 Sample Output
Sample Output
思路:
方法一:
对于GG的每个随从i如果他能杀死对方的哪些随从,那么在i与这些点之间进行建边,然后二分图匹配判断一下匹配数是不是n就好了。
时间复杂度:n^2
方法二:
对GG的随从按攻击力从小到大排序,将对方的随从按血量从小到大排序,然后每个随从攻击他所能杀死的随从中攻击力最大且不大于他的血量的随从(可以在线段树中进行操作)。
时间复杂度:nlogn
Accept: 10 Submit: 48
Time Limit: 1000 mSec Memory Limit : 32768 KB
 Problem Description
Problem Description
为了帮助柯南回到一米七四,阿笠博士夜以继日地研究APTX4869的解药。他得出了如下结果:
1.解药由n种原料构成;
2.对于两种不同的的原料a,b,它们之间有个影响值f(a,b);
3.需要把原料分成两个部分X,Y,每部分中至少有一种原料;
4.解药的效果由分别属于X,Y的原料之间,最小的影响值决定,即
效果=min{f(a,b)|a∈X,b∈Y)}
博士需要你帮忙求出:在所有的方案中,最大的效果值可以是多少?
 Input
Input
多组数据(<=10),处理到EOF。
每组数据输入第一行为一个正整数n。
接下去是一个n行n列的整数矩阵,同一行的数以空格隔开。矩阵第i行j列表示第i种和第j种材料的影响值f(i,j)。给出的矩阵是对称的,即f(i,j)=f(j,i)。当i=j时,f(i,i)没有意义,矩阵该处的值为-1。
2<=n<=800。当i!=j时,0<=f(i,j)<=1000000;当i=j时,f(i,j)=-1。
 Output
Output
每组数据输出一行,表示最大可能的效果值。
 Sample Input
Sample Input
 Sample Output
Sample Output
思路:
该题的另外一个题意便是将一个环分成两个环,这两个环之间边的最小值的最大值是多少
思路一:
二分答案,
二分过程思路:
用并查集把边长小于答案的点联合起来,判断这时候是不是只有一个环
思路二:
按边从小到大排序,处理出加入最后一个边使全部点连成一个环的那条边的长度便可以了
Accept: 7 Submit: 119
Time Limit: 1000 mSec Memory Limit : 32768 KB
 Problem Description
Problem Description
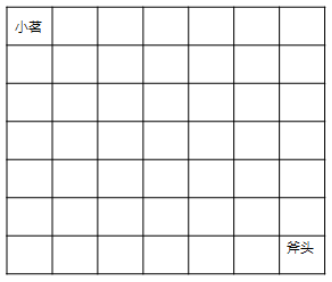
小茗同学正在玩牧场物语。该游戏的地图可看成一个边长为n的正方形。
小茗同学突然心血来潮要去砍树,然而,斧头在小茗的右下方。
小茗是个讲究效率的人,所以他会以最短路程走到右下角,然后再返回到左上角。并且在路上都会捡到/踩到一些物品,比如说花朵,钱和大便等。
物品只能被取最多一次。位于某个格子时,如果格子上还有物品,就一定要取走。起点和终点上也可能有物品。
每种物品我们将为其定义一个价值,当然往返之后我们取得的物品的价值和越大越好。但是小茗同学正在认真地玩游戏,请你计算出最大的价值和。
 Input
Input
多组数据(<=10),处理到EOF。
第一行输入正整数N(N≤100),表示正方形的大小。
接下来共N行,每行N个整数Ai,j(|Ai,j|≤10^9),表示相应对应位置上物品的价值。值为0表示没有物品。
 Output
Output
每组数据输出一个整数,表示最大价值和。
 Sample Input
Sample Input
 Sample Output
Sample Output
思路:
不难看出,可转化为从(1,1)到(n,n)走两次所经过的方格的和最多能有多少
经分析可知,每个方格的横坐标纵坐标之和就是所经过的时间,
dp[t][i][j]表示走了时间t,两个人的横纵坐标分别为i,j;那么他们的纵坐标便为t-i+1,t-j+1;
同时,如果两个人走到一个点,他们所经过的时间必定相同
所以转移方程为dp[t][i][j]=max1(dp[t-1][i][j],dp[t-1][i-1][j],dp[t-1][i][j-1],dp[t-1][i-1][j-1])+(i==j?a[i][t+1-i]:(a[i][t+1-i]+a[j][t+1-j])));
Accept: 7 Submit: 44
Time Limit: 1000 mSec Memory Limit : 32768 KB
 Problem Description
Problem Description
黑暗之王有一片棋盘般的疆土,这片疆土有2*10^9行,有2*10^9列。假设这块疆土的行从上到下编号1到2*10^9,它的列从左到右也编号1到2*10^9。我们可以把第i行第j列的方格记为坐标(i,j)。
但是这偌大棋盘只有被给的N个线状区域才是允许通行的。每个线状区域被三个参数描述,ri,ai,bi(ai<= bi)。ri代表给定线状区域的行编号,ai代表线状区域的起始列编号,bi代表末尾编号。
现在国王想要从一个给定坐标方格(x0,y0)通过最小移动步数到达终点坐标方格(x1,y1),而且只能通过上述给出的允许通行的线状区域。
国王移动一步只能发生在相邻的方格之间。此外,如果两个方格至少共享一个点我们便认为他们相邻。
 Input
Input
有多组数据(<=30),处理到文件尾(EOF)。
每组数据第一行包含四个整数,x0, y0, x1, y1(1 <= x0, y0, x1, y1 <= 2*10^9),分别代表国王的初始坐标和终点坐标。
第二行有一个整数N (1 <= N <= 10^5),代表有N条可通行的线状区域。
接下里会有N行,第i行包含三个整数,ri,ai, bi (1 <= ri, ai bi <= 2*10^9),含义看题面。
数据允许线状区域会有交叉或者嵌套。
数据保证国王的起点方格和终点方格都是可通行的,并且两个区域不相同。另外保证所有线状区域的的长度总和不超过10^5。
1 <= x0, y0, x1, y1, ri, ai, bi<= 2*10^9,1 <= N <= 10^5
 Output
Output
如果没有一条道路使得国王从起始区域到达终点区域,则输出 -1。
否则,则输出国王的从起始区域到达终点区域的最小步数。
 Sample Input
Sample Input
 Sample Output
Sample Output
思路:因为只有10^5个点,所以我们可以先处理出哪些点是可以走的,然后从终点到起点,一个简单的bfs便可以了。
Accept: 4 Submit: 8
Time Limit: 1500 mSec Memory Limit : 131072 KB
 Problem Description
Problem Description
有一颗n个节点的树,节点编号1-n。树上每条边都有一个权值,现在给出q个询问,每次询问给出两个点u,v,表示一条端点为u,v的路径,现在要询问这条路径上的边的权值的中位数是多少,如果路径长度为偶数,那么此时有两个中位数,取较小的那个进行输出。
 Input
Input
多组数据(<=5),处理到EOF。
第一行输入两个数n、q,接下来n-1行每行三个数u,v,w,表示u和v之间有一条边,并且其权值为w,接下来q行,每行两个数u、v,表示询问的路径。
1<=n,q<=5*10^4
1<=u、v<=n,u!=v
0<=w<=10^5
 Output
Output
每组数据输出q行,每行一个数,表示答案。
 Sample Input
Sample Input
 Sample Output
Sample Output
思路:
我们可以把边转化为点的值,然后利用树上第k大便可以简单的解决了