树状数组详解(图形学算法)
目录
一、从图形学算法说起
1、Median Filter 概述
2、r pixel-Median Filter 算法
3、一维模型
4、数据结构的设计
5、树状数组华丽登场
二、细说树状数组
1、树 or 数组?
2、结点的含义
3、求和操作
4、更新操作
5、lowbit函数O(1)实现
6、小结
三、树状数组的经典模型
1、PUIQ模型
2、IUPQ模型
3、逆序模型
4、二分模型
5、再说Median Filter
6、多维树状数组模型
四、树状数组题集整理
一、从图形学算法说起
1、Median Filter概述
Median Filter 在现代的图形处理中是非常基础并且广泛应用的算法 (翻译叫 中值滤波器,为了不让人一看到就觉得是高深的东西,还是选择了使用它的英文名,更加能让人明白是个什么东西) ,如图一-1-1,基本就能猜到这是一个什么样的算法了,可以简单的认为是PS中的"模糊"那个操作。
图一-1-1
2、r pixel-Median Filter算法
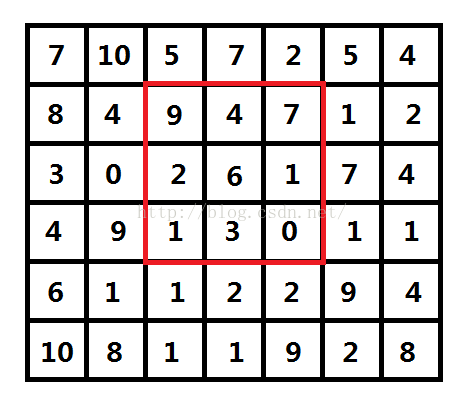
首先对于一张宽为W,高为H的图片,每个像素点存了一个颜色值,这里为了把问题简化,先讨论黑白图片,黑白图片的每个像素值可以认为是一个[0, 255]的整数(如图一-1-2,为了图片看起来不是那么的密密麻麻,像素值的范围取了[0, 10])。
r pixel-Median Filter
算法描述如下:
对于每个第i行第j列的像素点p(i, j),像四周扩展一个宽和高均为(2r + 1)的矩形区域,将矩形区域内的像素值按非降序排列后,用排在最中间的那个数字取代原来的像素点p(i, j)的值( 边界的那圈不作考虑 ),下文会将排在最中间的那个数字称为这个序列的
中位数
。
图一-1-2
如图一-1-2,r = 1,红框代表(2, 3) (下标从0计数,行优先)这个像素点所选取的2r + 1的矩形区域,将内中数字进行非降序排列后,得到
[0 1 1 2 3 4 6 7 9],所以(2, 3)这个像素点的值将从 6 变成 3。
这样就可以粗略得到一个时间复杂度为O(n^4
logn
)的算法(枚举每个像素点,对于每个像素点取矩形窗口元素排序后取中值)。n代表了图片的尺寸,也就是当图片越大,这个算法的执行效率就越低,而且增长迅速。那么如何将这个算法进行优化呢?如果对于二维的情况不是很容易下手的话,不妨先从一维的情况进行考虑。
3、一维模型
将问题转化成一维,可以描述成:给定
n
(n <= 100000)个范围在[0, 255]的数字序列a[i] (1 <= i < = n)和一个值
r
(2r+1 <= n),对于所有的a[k] (r+1 <= k <= n-r),将它变成 a[k-r ... k+r] 中的中位数。
a[1...7] = [1 7 6 4 3 2 1] r = 2
d[3] = median( [1 7 6 4 3] ) = 4
d[4] = median( [7 6 4 3 2] ) = 4
d[5] = median( [6 4 3 2 1] ) = 3
所以原数组就会变成a[1..7] = [1 7
4 4 3
2 1]
那么总共需要计算的元素为n-2r,取这些元素的左右r个元素的值需要2r+1次操作,(n-2r)*(2r+1) 当r = (n-1)/4 时取得最大值,为 (n+1)^2 / 4,再加上排序的时间复杂度,所以最坏情况的时间复杂度为O( n^2 logn )。n的范围不允许这么高复杂度的算法,尝试进行优化。
考虑第i个元素的2r+1区域
a[ i-r ... i+r ]
和第i+1个元素的2r+1区域
a[ i+1-r ... i+1+r ]
,后者比前者少了一个元素a[i-r],多了一个元素a[i+1+r],其它元素都是一样的,那么在计算第i+1个元素的情况时如何利用第i个元素的情况就成了问题的关键。
4、数据结构的设计
我们现在假设有这样一种数据结构,可以支持以下三种操作:
1、
插入(Insert),将一个数字插入到该数据结构中;
2、删除(Delete), 将某个数字从该数据结构中删除;
3、询问(Query), 询问该数据结构中存在数字的中位数;
如果这三个操作都能在O( log(n) )或者O(1)的时间内完成,那么这个问题就可以完美解决了。具体做法是:
首先将a[1...2r+1]这些元素都插入到该数据结构中,然后询问中位数替换掉a[r+1],再删除a[1],插入a[2r+2],询问中位数替换掉a[r+2],以此类推,直到计算完第n-r个元素。所有操作都在O( log(n) ) 时间内完成的话,总的时间复杂度就是O( nlogn )。
我们来看什么样的数据结构可以满足这三条操作都在O( log(n) )的时间内完成,考虑每个数字的范围是[0, 255],如果我们将这些数字映射到一个线性表中(即 HASH表),
插入和删除操作都可以做到O(1)。
具体得,用一个辅助数组d[256],插入a[i]执行的是d[ a[i] ] ++,删除a[i]执行的是 d[ a[i] ] --;询问操作是对d数组进行顺序统计,顺序枚举i,找到第一个满足
sum{d[j] | 1 <= j <= i} >= r+1的 i 就是所求中位数,这样就得到了一个时间复杂度为O(Kn)的算法,其中K是数字的值域(这里讨论的问题值域是256)。
相比之前的算法,这种方法已经前进了一大步,至少n的指数下降了大于一个数量级,但是也带来了一个问题,如果数字的值域很大,复杂度还是会很大,所以需要更好的算法支持。
5、树状数组华丽登场
这里引入一种数据结构 - 树状数组 ( Binary Indexed Tree,BIT,二分索引树 ),它只有两种基本操作,并且都是操作线性表的数据的:
1、
add( i, 1 ) (1<=i<=n) 对第i个元素的值自增1 O(logn)
2、sum( i ) (1<=i<=n) 统计[1...i]元素值的和 O(logn)
试想一下,如果用HASH来实现这两个函数,那么1的复杂度是O(1),而2的复杂度就是O(n)了,而树状数组实现的这两个函数可以让两者的复杂度都达到O(logn),具体的实现先卖个关子,留到第二节着重介绍。
有了这两种操作,我们需要将它们转化成之前设计的数据结构的那三种操作,首先:
1、插入(Insert),对应的是 add(i, 1),时间复杂度O( logn )
2、删除(Delete), 对应的是 add(i, -1), 时间复杂度O( logn )
3、询问(Query), 由于sum( i )能够统计[1...i]元素值的和,换言之,它能够得到我们之前插入的数据中小于等于i的数的个数,那么如果能够知道sum(i) >= r + 1的最小的i,那这个i就是所有插入数据的中位数了(因为根据上文的条件,插入的数据时刻保证有2r+1个)。因为sum(i)是关于 i 的递增函数,所以基于单调性我们可以二分枚举i (1 <= i <= n),得到最小的 i 满足sum(i) >= r + 1,每次的询问复杂度就是 O( logn * logn )。 一个logn是二分枚举的复杂度,另一个logn是sum函数的复杂度。
这样一来,一维的Median Filter模型的整体时间复杂度就降到了O(n * logn * logn),已经是比较高效的算法了。
接下来就是要来说说树状数组的具体实现了。
二、细说树状数组
1、树 or 数组 ?
名曰树状数组,那么究竟它是树还是数组呢?数组在物理空间上是连续的,而树是通过父子关系关联起来的,而树状数组正是这两种关系的结合,首先在存储空间上它是以数组的形式存储的,即下标连续;其次,对于两个数组下标x,y(x < y),如果x + 2^k = y (k等于x的二进制表示中末尾0的个数),那么定义(y, x)为一组树上的父子关系,其中y为父结点,x为子结点。
图二-1-1
如图二-1-1,其中A为普通数组,C为树状数组(C在物理空间上和A一样都是连续存储的)。树状数组的第4个元素C4的父结点为C8 (4的二进制表示为"100",所以k=2,那么4 + 2^2 = 8),C6和C7同理。C2和C3的父结点为C4,同样也是可以用上面的关系得出的,那么从定义出发,奇数下标一定是叶子结点。
2、结点的含义
然后我们来看树状数组上的结点Ci具体表示什么,这时候就需要利用树的递归性质了。我们定义Ci的值为它的所有子结点的值 和 Ai 的总和,之前提到当i为奇数时Ci一定为叶子结点,所以有Ci = Ai ( i为奇数 )。从图中可以得出:
C1 = A1
C2 = C1 + A2 = A1 + A2
C3 = A3
C4 = C2 + C3 + A4 = A1 + A2 + A3 + A4
C5 = A5
C6 = C5 + A6 = A5 + A6
C7 = A7
C8 = C4 + C6 + C7 + A8 = A1 + A2 + A3 + A4 + A5 + A6 + A7 + A8
建议直接看C8,因为它最具代表性。
我们从中可以发现,其实Ci还有一种更加普适的定义,它表示的其实是一段原数组A的连续区间和。根据定义,右区间是很明显的,一定是i,即Ci表示的区间的最后一个元素一定是Ai,那么接下来就是要求Ci表示的第一个元素是什么。从图上可以很容易的清楚,其实就是顺着Ci的最左儿子一直找直到找到叶子结点,那个叶子结点就是Ci表示区间的第一个元素。
更加具体的,如果i的二进制表示为 ABCDE1000,那么它最左边的儿子就是 ABCDE0100,这一步是通过结点父子关系的定义进行逆推得到,并且这条路径可以表示如下:
ABCDE1000 => ABCDE0100 => ABCDE0010 => ABCDE0001
这时候,ABCDE0001已经是叶子结点了,所以它就是Ci能够表示的第一个元素的下标,那么我们发现,如果用k来表示i的二进制末尾0的个数,Ci能够表示的A数组的区间的元素个数为2^k
,又
因为区间和的最后一个数一定是Ai,所以有如下公式:
Ci = sum{ A[j] | i - 2^k + 1 <= j <= i } (帮助理解:将j的两个端点相减+1 等于2^k)
3、求和操作
明白了Ci的含义后,我们需要通过它来求sum{ A[j] | 1 <= j <= i },也就是之前提到的sum(i)函数。为了简化问题,用一个函数lowbit(i)来表示2^k
(
k等于i的二进制表示中末尾0的个数)。那么:
sum(i) = sum{ A[j] | 1 <= j <= i }
= A[1] + A[2] + ... + A[i]
= A[1] + A[2] + A[i-2^k
] + A[i-
2^k
+1] + ... + A[i]
= A[1] + A[2] + A[i-2^k
] + C[i]
= sum(i - 2^k
) + C[i]
= sum( i - lowbit(i) ) + C[i]
由于C[i]已知,所以sum(i)可以通过递归求解,递归出口为当i = 0时,返回0。sum(i)函数的函数主体只需要一行代码:
int sum(int x){
return x ? C[x]+ sum( x - lowbit(x)):0;
}
观察 i - lowbit(i),其实就是将i的二进制表示的最后一个1去掉,最多只有log(i)个1,所以求sum(n)的最坏时间复杂度为O(logn)。由于递归的时候常数开销比较大,所以一般写成迭代的形式更好。写成迭代代码如下:
int sum(int x){
int s =0;
for(int i = x; i ; i -= lowbit(i)){
s += c[i][j];
}
return s;
}
4、更新操作
更新操作就是之前提到的add(i, 1) 和 add(i, -1),更加具体得,可以推广到add(i, v),表示的其实就是 A[i] = A[i] + v。但是我们不能在原数组A上操作,而是要像求和操作一样,在树状数组C上进行操作。
那么其实就是求在Ai改变的时候会影响哪些Ci,看图二-1-1的树形结构就一目了然了,Ai的改变只会影响Ci及其祖先结点,即A5的改变影响的是C5、C6、C8;而A1的改变影响的是C1、C2、C4、C8。
也就是每次add(i, v),我们只要更新Ci以及它的祖先结点,之前已经讨论过两个结点父子关系是如何建立的,所以给定一个x,一定能够在最多log(n) (这里的n是之前提到的值域) 次内更新完所有x的祖先结点,add(i, v)的主体代码(去除边界判断)也只有一行代码:
void add(int x,int v){
if(x <= n){
C[x]+= v, add( x + lowbit(i), v );
}
}
void
add
(
int
x
,
int
v
){
for
(int
i
=
x
;
i
<
=
n
;
i
+
=
lowbit
(
i
)
)
{
C
[i] += v;
}
}
5、lowbit函数O(1)实现
上文提到的两个函数sum(x)和add(x, v)都是用递归实现的,并且都用到了一个函数叫lowbit(x),表示的是2k,其中k为x的二进制表示末尾0的个数,那么最简单的实现办法就是通过位运算的右移,循环判断最后一位是0还是1,从而统计末尾0的个数,一旦发现1后统计完毕,计数器保存的值就是k,当然这样的做法总的复杂度为O( logn ),一个32位的整数最多可能进行31次判断(这里讨论整数的情况,所以符号位不算)。
这里介绍一种O(1)的方法计算2k的方法。
来看一段补码小知识:
清楚补码的表示的可以跳过这一段,计算机中的符号数有三种表示方法,即
原码
、
反码和补码。三种表示方法均有符号位和数值位两部分,符号位都是用0表示“正”,用1表示“负”,而数值位,三种表示方法各不相同。
这里只讨论整数补码的情况,
在计算机系统中,数值一律用补码来表示和存储。原因在于,使用补码,可以将符号位和数值域统一处理;同时,加法和减法也可以统一处理。整数补码的表示分两种:
正数:正数的补码即其二进制表示;
例如一个8位二进制的整数+5,它的补码就是 00000101 (标红的是符号位,0表示"正",1表示“负”)
负数:负数的补码即将其整数对应的二进制表示所有位取反(包括符号位)后+1;
例如一个8位二进制的整数-5,它的二进制表示是00000101,取反后为11111010,再+1就是1
1111011,这就是它的补码了。
下面的等式可以帮助理解补码在计算机中是如何工作的
+5 + (-5) = 00000101 + 11111011 = 1 00000000 (溢出了!!!) = 0
这里的加法没有将数值位和符号位分开,而是统一作为二进制位进行计算,由于表示的是8进制的整数,所以多出的那个最高位的1会直接舍去,使得结果变成了0,而实际的十进制计算结果也是0,正确。
补码复习完毕,那么来看下下面这个表达式的含义:
x & (-x) (其中 x >= 0)
首先进行&运算,我们需要将x和-x都转化成补码,然后再看&之后会发生什么,我们假设 x 的二进制表示的末尾是连续的 k 个 0,令x的二进制表示为
X0X1X2…Xn-2Xn-1, 则 {X
i
= 0 | n-k <= i < n}, 这里的X0表示符号位。
x 的补码就是由三部分组成:
(0)(
X1X2…Xn-k-1)(k个0)
其中
Xn-k-1为1,因为末尾是k个0,如果它为0,那就变成k+1个0了。
-x的补码也是由三部分组成: (1)(
Y1Y2…Yn-k-1)(k个0) 其中
Yn-k-1为1,其它的
Xi和
Yi相加为1,
想
想补码是怎么计算的就明白了。
那么
x & (-x)
也就显而易见了,由两部分组成
(1)(k个0)
,
表示成十进制为
2k
啦。
由于&的优先级低于-,所以代码可以这样写:
int lowbit(int x) {
return x & -x;
}
6、小结
至此,树状数组的基础内容就到此结束了,三个函数就诠释了树状数组的所有内容,并且都只需要一行代码实现,单次操作的时间复杂度为O( log(n) ),空间复杂度为O(n),所以它是一种性价比非常高的轻量级数据结构。
树状数组解决的基本问题是 单点更新,成端求和。上文中的sum(x)求的是[1, x]的和,如果需要求[x, y]的和,只需要求两次sum函数,然后相减得到,即sum(y) - sum(x-1)。
下面一节会通过一些例子来具体阐述树状数组的应用场景。
三、树状数组的经典模型
1、PUIQ模型
【例题1】一个长度为n(n <= 500000)的元素序列,一开始都为0,现给出三种操作:
1. add x v : 给第x个元素的值加上v; ( a[x] += v )
2. sub x v : 给第x个元素的值减去v; ( a[x] -= v )
3. sum x y: 询问第x到第y个元素的和; ( print sum{ a[i] | x <= i <= y } )
这是树状数组最基础的模型,1和2的操作就是对应的单点更新,3的操作就对应了成端求和。
具体得,1和2只要分别调用add(x, v)和add(x, -v), 而3则是输出sum(y) - sum(x-1)的值。
我把这类问题叫做PUIQ模型(Point Update Interval Query 点更新,段求和)。
2、IUPQ模型
【例题2】一个长度为n(n <= 500000)的元素序列,一开始都为0,现给出两种操作:
1. add x y v : 给第x个元素到第y个元素的值都加上v; ( a[i] += v, 其中 x <= i <= y )
2. get x: 询问第x个元素的值; ( print a[x] )
这类问题对树状数组稍微进行了一个转化,但是还是可以用add和sum这两个函数来解决,对于操作1我们只需要执行两个操作,即add(x, v)和add(y+1, -v);而操作2则是输出sum(x)的值。
这样就把区间更新转化成了单点更新,单点求值转化成了区间求和。
我把这类问题叫做IUPQ模型(Interval Update Point Query 段更新,点求值)。