不相交集生成随机迷宫

（一）数学概念

若对于每一对元素(a,b)，a,b ∈S,aRb或者为true或者为false,则称在集合S上定义关系R。如果aRb为true，则说明两者有关系。

等价关系是指满足以下三个性质的关系R

a） （自反性）对于所有属于S的a，aRa

b）（对称性） aRb 当且仅当 b R a

c） （传递性）若aRb 并且 b R a 意味着 aRc

对于集合S划分，取任意两个等价类，Si与Sj，如果Si∩Sj = ∅，则称这些集合不相交。

对于不相交集，有两种操作，Union/Find操作。

Find操作用来找包含给定元素的集合（等价类）名字。

Union操作用来把两个等价类合并成一个新的等价类。

（二）基本数据结构

采用树来表示每一个集合（等价类），因为树上的元素都有一个共同的根。

定义Union(X, Y)操作，将X,Y合并成一个新的等价类，且X做为根

union操作步骤如下所示

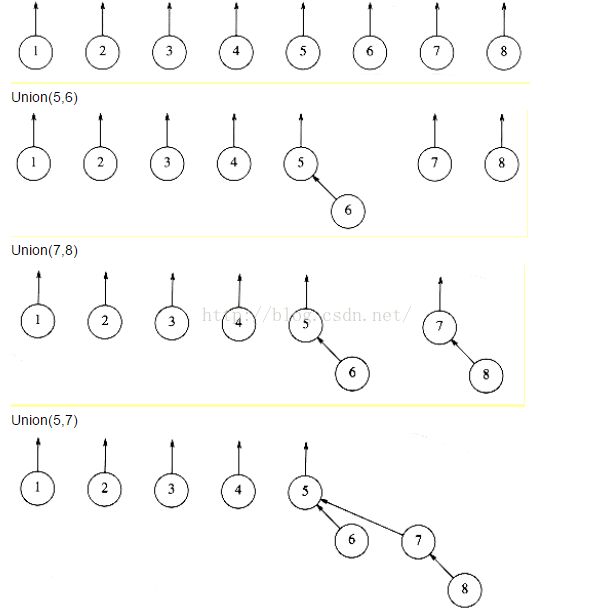
按照这种运算，经过N-1次合并后，最坏能生成一棵深度为N-1的树，时间复杂度为O（N）

采用数组结构来保存每个元素所在的等价关系，数组的第一个成员s[i]表示元素i的父节点。如果元素i所在的集合只有一个元素，则s[i] = 0。上述的森林用数组表示如下

定义Find(x)操作，该操作为递归过程，如：Find(8), 父亲为7， 执行Find(7)，父亲为5，执行Find(5)，对应值为0，表示5为树根，递归结束。

判断6,8是否有关系，实为判断Find(8) == Find(6)。

（三）优化union操作

为了避免union合并造成树的深度过大，每次可以让深度小的树成为深的树的子树。数组值可以让根的值为负值，其绝对值代表深度。

对于上次图表，假设继续执行Union(4，5），两种操作对比如下：

（四）不相交集的ADT实现

public final class DisJoinSet {

	private int[] eleRoots;
	
	public DisJoinSet(int num){
		this.eleRoots = new int[num];
		for(int i=0;i<num;i++){
			getEleRoots()[i] = -1;
		}
	}
	
	public int find(int ele){
		if(getEleRoots()[ele] < 0){
			return ele;
		}
		
		return find(getEleRoots()[ele]);
	}
	
	public void union(int root1,int root2){
		//让深度较小的树成为深度较大的树的子树
		if(getEleRoots()[root1] > getEleRoots()[root2]){
			getEleRoots()[root1] = root2;
		}else{
			if(getEleRoots()[root1] == getEleRoots()[root2]){//深度一样，则更新深度
				getEleRoots()[root1]--;
			}
			getEleRoots()[root2] = root1;
		}
	}

	public int[] getEleRoots() {
		return eleRoots;
	}

}

（五）使用不相交集生成随机迷宫

假设迷宫的起点在界面的左上点，终点在界面的右下点。我们可以把迷宫看成一个m*n的矩阵。矩阵一开始四周全部被墙壁隔开。为此，我们不断地在迷宫内随机选择一个点，如果该点与周围某一点之间存在一面墙，我们就把这面墙拆掉。重复这个过程，直到起点和终点落在同一个等价类（即起点和终点之间存在可达关系）。相关代码如下

import java.awt.Color;
import java.awt.Graphics;
import java.util.ArrayList;
import java.util.List;
import java.util.Random;

import javax.swing.JFrame;


public class Maze extends JFrame{

	private int row;//行数
	private int col;	//列数
	private DisJoinSet disjSet;
	private int winHeight=700;  
	private int winWidth=780;  
	
	public Maze(int row,int col){
		this.row = row;
		this.col = col;
		this.setTitle("迷宫");  
		this.setSize(winWidth,winHeight);  
		this.setVisible(true);  
		this.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE);  
	}
	
	public static void main(String[] args) {
		int rowCount = 50;
		int colCount = 50;
		Maze maze = new Maze(rowCount,colCount);

	}

	public void paint(Graphics g){  
		super.paint(g);
		//背景为白色  
		g.setColor(Color.white);  
		g.fillRect(0, 0, winWidth, winHeight);  
		g.setColor(Color.black);  
		final int extraWidth = 20;
		final int cellWidth = (winWidth-2*extraWidth)/row;//定义每个格子的宽度
		final int cellHeight = (winHeight-4*extraWidth)/col;//定义每个格子的高度
		for(int i=0;i<row;i++)  {
			for(int j=0;j<col;j++)  
			{  
				//初始化m*n矩阵格子
				g.drawRect(i*cellWidth+extraWidth,j*cellHeight+2*extraWidth, cellWidth, cellHeight);  
			}  
		}
		
		int lastPos = getLastElePos();//迷宫最后一个格式的代表数字
		//起点，终点特殊处理
		g.setColor(Color.red);  
		g.fillRect(extraWidth, 2*extraWidth, cellWidth, cellHeight);
		g.fillRect((lastPos% row)*cellWidth + extraWidth,(lastPos/ row)*cellHeight + 2*extraWidth, cellWidth, cellHeight);
		
		this.setDisjSet(new DisJoinSet(row*col));
		g.setColor(Color.white);  //用后景色擦色
		while(disjSet.find(0) != disjSet.find(lastPos)){//如果起点和终点还没在同一个等价类
			/*
			 *  在迷宫内随机挖一个点，再找到该点周围一点，使这两个点落在同一个等价类
			 */
			Random random = new Random();
			int randPos = random.nextInt(lastPos+1);//+1是为了能随机到最后一位
			int rowIndex = randPos % row;
			int colIndex = randPos / col;
			List<Integer> neighborPos = getNeighborNums(rowIndex, colIndex) ;
			int randNeighbor = neighborPos.get(random.nextInt(neighborPos.size()));

			if(disjSet.find(randPos)  ==  disjSet.find(randNeighbor)){//两点在同一个等价类
				continue;
			}else{
				int aRoot = disjSet.find(randPos);
				int bRoot = disjSet.find(randNeighbor);
				disjSet.union(aRoot, bRoot);
				int maxNum = Math.max(randPos, randNeighbor);//取得较大点
				int x1=0,y1=0,x2=0,y2=0;  
				if(Math.abs(randPos-randNeighbor) == 1){//说明在同一行，用竖线隔开
					x1= x2=(maxNum% row)*cellWidth + extraWidth;
					y1=(maxNum/ row)*cellHeight + 2*extraWidth;
					y2=y1+cellHeight;
				}else{//说明在同一列，用横线隔开
					y1=y2=(maxNum/ row)*cellHeight + 2*extraWidth;
					x1=(maxNum% row)*cellWidth + extraWidth;
					x2=x1+cellWidth;
				}
//				System.err.println("x1="+x1+",x2="+x2+",y1="+y1+",y2="+y2);
				 g.drawLine(x1, y1, x2, y2);
			}
		}
		
	}

	/**
	 *  取得目标坐标点周围四个有效点
	 */
	public List<Integer> getNeighborNums(int rowIndex,int colIndex){
		List<Integer> neighborPos = new ArrayList<Integer>(4);
		//右元素
		if(isPointInMaze(rowIndex+1,colIndex)){
			neighborPos.add(getCoordinateNum(rowIndex+1,colIndex));
		}
		//下元素
		if(isPointInMaze(rowIndex,colIndex+1)){
			neighborPos.add(getCoordinateNum(rowIndex,colIndex+1));
		}
		//左元素
		if(isPointInMaze(rowIndex-1,colIndex)){
			neighborPos.add(getCoordinateNum(rowIndex-1,colIndex));
		}
		//上元素
		if(isPointInMaze(rowIndex,colIndex-1)){
			neighborPos.add(getCoordinateNum(rowIndex,colIndex-1));
		}

		return neighborPos;
	}
	public int getLastElePos(){
		return row*col-1;
	}

	public DisJoinSet getDisjSet() {
		return disjSet;
	}

	public void setDisjSet(DisJoinSet disjSet) {
		this.disjSet = disjSet;
	}

	/**
	 *  根据坐标返回对应的值
	 *  例如在4*3矩阵，(0，0)返回0;(3,2)返回10
	 */
	public int getCoordinateNum(int x,int y){
		return y*col + x;
	}
	

	/**
	 *  判断给定坐标是否在迷宫矩阵内
	 */
	public boolean isPointInMaze(int x,int y){
		if(x < 0 || y < 0) return false;
		return x < row && y <col;
	}
}

程序执行结果

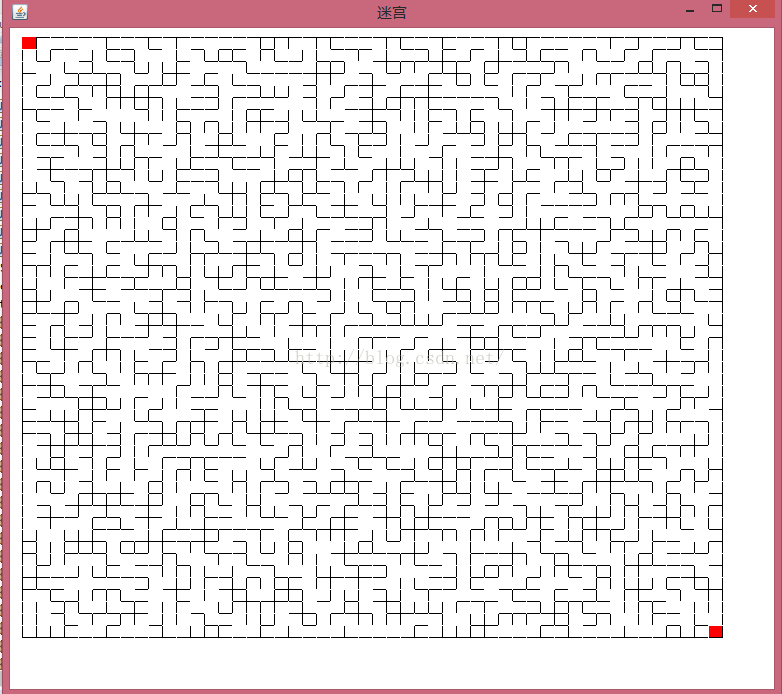
参考文献

[ 1] 佛罗里达国际大学.数据结构与算法分析Java语言描述.机械工业出版社,219-233