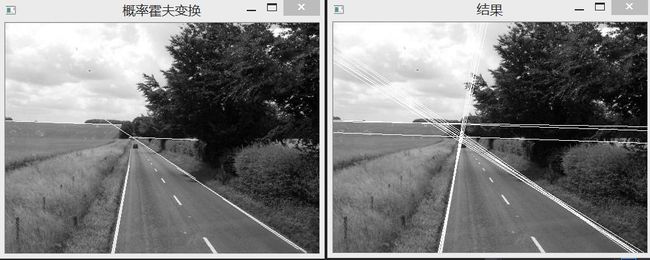
Opecv霍夫变换检测直线
一些概念的东西:
一条直线可以表示为:
y=ax+b,其中a、b为常数,(x,y)表示一个点,是变量。这个式子表示了 一条直线和直线上的点的关系。坐标系为x轴和y轴,图形为一条线。
换一个出发点,考虑一个点和通过该点的直线的关系。
假设已知某一个(x1,y1),x1和y1为常量。下式表示所有通过点(x1,y1)的直线。
y1=a*x1+b,其中a、b是变量,x1和y1为常量,表示点(x1,y1)。为了看起来方便,我们可以将该式子变为
a=-b/x1+y1/x1,其中,y1/x1为常数项。这个式子表示了通过固定点的直线。坐标系为a轴和b轴,图形为一条线。
在(a,b)坐标系空间中,假设两条直线相交于点(a1,b1)。该点即表示(x,y)坐标系空间中的一条直线 y=a1*x+b1。(a,b)坐标系空间中,相交于点(a1,b1)的两条直线,表示在(x,y)坐标系空间中直线y=a1*x+b1上的两个点。
用霍夫变换检测直线便基于以上原理:
将原空间中的点,在新空间中表示成一条直线。新空间中多条直线相交的点,为原空间的直线。新空间中越多的直线交于一点,该点表示的直线(原空间)的可信度越高。取可信度高于设定阈值的点(原空间中的直线),即检测出了一副图像中的直线。
在霍夫变换检测直线的实际应用中,由于除数不能为0的缘故(-b/x1,x1不能为0)不采用(x,y)坐标空间表示直线,而是用极坐标空间(р,θ)替代(x,y)空间。直线描述方程如下:
p=x cosθ + y sinθ (x,y为变量, p,θ 为常量)
方法与上述类似,将x和y看为常量,p,θ 看为变量。其余的概念相同。
这里只简单讲了一下相关的概念。霍夫变换还有一个改进算法,叫概率霍夫变换,另外霍夫变换可以检测其他形状,例如圆。想了解的童鞋,可以自行百度。
代码:
源.cpp
#include"ClassLineFinder.h"
int main()
{
cv::Mat image = cv::imread("D:/images/road.jpg", 0);
//霍夫变换直线检测
lineFinder lh;
lh.line_hough(image);
lh.showResult();
//概率霍夫变换直线检测
lh.set(100, 20, 80);
lh.houghP_line(image);
lh.showResult(0);
//霍夫变换检测圆
cv::Mat image2 = cv::imread("D:/images/chariot.jpg",0);
lh.hough_circle(image2);
lh.showResult(0.0);
cv::waitKey(0);
return 0;
}ClassLineFinder.h
#ifndef LINEFINDER_H
#define LINEFINDER_H
#include<opencv2\highgui\highgui.hpp>
#include<opencv2\imgproc\imgproc.hpp>
#include<opencv2\core\core.hpp>
#define PI 3.1415926
class lineFinder
{
private:
//边缘图像,用canny检测物体边缘
cv::Mat contours;
//结果
cv::Mat result;
//步进尺寸
double deltaRho;
double deltaTheta;
//最小投票数
int minVote;
//直线最小长度
double minLength;
//最大缺口数
double maxGap;
public:
lineFinder() :deltaRho(1), deltaTheta(PI / 180), minVote(10),
minLength(0.), maxGap(0.){}
//霍夫变换检测直线
void line_hough(const cv::Mat &image)
{
image.copyTo(result);
cv::Canny(image, contours, 125, 350);
std::vector<cv::Vec2f> line;
cv::HoughLines(contours, line, 1, PI / 180, 80);
std::vector<cv::Vec2f>::const_iterator it = line.begin();
while (it != line.end())
{
float rho = (*it)[0];
float theto = (*it)[1];
if (theto<PI / 4 || theto>3.*PI / 4.)
{
cv::Point p1(rho / cos(theto), 0);
cv::Point p2((rho - result.rows*sin(theto)) / cos(theto), result.rows);
cv::line(result, p1, p2, cv::Scalar(255), 1);
}
else
{
cv::Point p1(0, rho / sin(theto));
cv::Point p2(result.cols,(rho - result.cols*cos(theto)) / sin(theto));
cv::line(result, p1, p2, cv::Scalar(255), 1);
}
++it;
}
}
//概率霍夫变换检测直线
void houghP_line(const cv::Mat &image)
{
std::vector<cv::Vec4i> line;
image.copyTo(result);
cv::Canny(image, contours, 125, 350);
cv::HoughLinesP(contours, line, deltaRho, deltaTheta, minVote, minLength, maxGap);
std::vector<cv::Vec4i>::const_iterator it = line.begin();
while (it != line.end())
{
cv::Point pt1((*it)[0], (*it)[1]);
cv::Point pt2((*it)[2], (*it)[3]);
cv::line(result, pt1, pt2, cv::Scalar(255));
++it;
}
}
//霍夫变换检测圆
void hough_circle(const cv::Mat &image)
{
image.copyTo(result);
cv::GaussianBlur(image, image, cv::Size(5, 5), 1.5);
std::vector<cv::Vec3f> circles;
cv::HoughCircles(image, circles, CV_HOUGH_GRADIENT, 2,
50, 200, 100, 25, 100);
std::vector<cv::Vec3f>::const_iterator it = circles.begin();
while (it != circles.end())
{
cv::circle(result, cv::Point((*it)[0], (*it)[1]), (*it)[2],
cv::Scalar(255));
++it;
}
}
void set(double length, double gap,int min, double rho = 1, double theta = PI / 180)
{
minLength = length;
maxGap = gap;
deltaRho = rho;
deltaTheta = theta;
minVote = min;
}
void showResult()const
{
cv::imshow("结果", result);
}
void showResult(int i)const
{
cv::imshow("概率霍夫变换", result);
}
void showResult(double i)const
{
cv::imshow("霍夫变换检测圆", result);
}
};
#endif