How Many Pieces of Land题解

这道题首先要求土地可以分成多少部分的递推公式。现在给出过程：</p><p>

对于一个封闭图形，每增加一条内部线段就意味将原来的土地分割成了两部分，即增加了一个部分。

现在假定n个点总共最多可以分成An份，然后包含在这个N边形内部一共有Bn份。

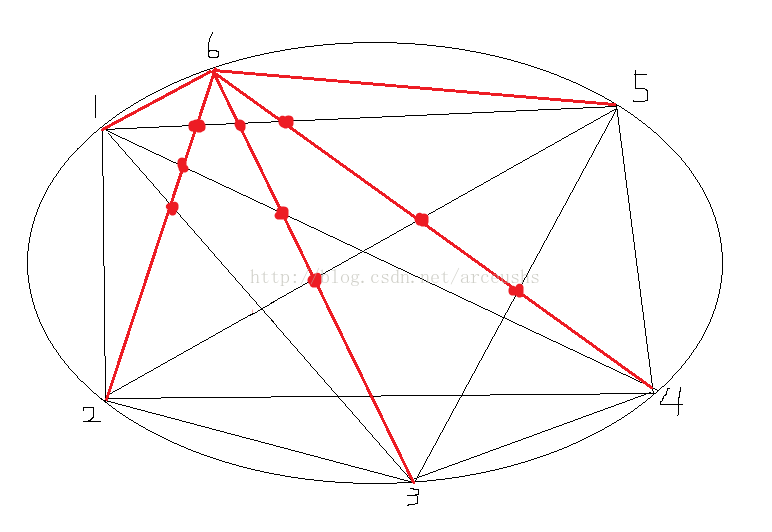
以上图为例，假定现在的五边形已经选好了，现在往其中添加第6个点，添加的点与它左边的第一个点1相连不会产生相交的点，与它左边的第二个点相连，会产生3个相交的点(这条线段左边有点1，右边有点5点4点3，因此会形成1*3个交点)，第6点与点3相连会产生4个交点（图中还有一个没有画出来）（这条线段左边有点1、2，右边有点4、5，因此形成2*2个交点），第6点和点4相连产生3个交点，与点5相连不会产生交点。</p><p>对于一条线段每增加n点，会形成n+1条线段，因此可知增加的第6个点会形成13条线段，也就意味着增加了13个部分，因此B6=（B5+1）+13（这里的+1是因为相对于原来的5边形的B5增加了1-5-6形成的一个部分）。

推而广之Bn=Bn-1+1+(1*(n-3)+1)+(2*(n-4)+1)+。。。。。+((n-3)*1+1)=Bn-1+(n-3)*(n-2)*(n-1)/6+n-2;又有An=Bn+n;n边形外部与椭圆会形成n各部分；因此An=An-1+(n-3)*(n-2)*(n-1)/6+n-1;然后从4开始计算就可以获得结果。剩下的就是大数计算了。代码没有经过优化。。。。。。。。

#include <iostream>
#include <cstring>
#include <string>
#include <sstream>
using namespace std;

string Add(string a,string b)
{
	int A[200];
	int B[200];
	int C[200];
	string c="";
	memset(A,0,sizeof(A));
	memset(B,0,sizeof(B));
	memset(C,0,sizeof(C));
	int len=a.size()>b.size()?a.size():b.size();
	for(int i=0;i<a.size();i++)
	{
		A[a.size()-1-i]=a[i]-'0';
	}
	for(int i=0;i<b.size();i++)
	{
		B[b.size()-1-i]=b[i]-'0';
	}
	for(int i=0;i<len;i++)
	{
		C[i]=A[i]+B[i];
	}
	for(int i=0;i<len;i++)
	{
		C[i+1]=C[i+1]+C[i]/10;
		C[i]=C[i]%10;
	}
	int k=199;
	while(C[k]==0)
	{
		k--;
	}
	for(int i=k;i>=0;i--)
	{
		stringstream tmp;
		string tmps;
		tmp<<C[i];
		tmp>>tmps;
		c=c+tmps;
	}
	return c;
}

string Sub(string a,string b)//假定a>b
{
	int A[200];
	int B[200];
	int C[200];
	string c="";
	memset(A,0,sizeof(A));
	memset(B,0,sizeof(B));
	memset(C,0,sizeof(C));
	int len=a.size()>b.size()?a.size():b.size();
	for(int i=0;i<a.size();i++)
	{
		A[a.size()-1-i]=a[i]-'0';
	}
	for(int i=0;i<b.size();i++)
	{
		B[b.size()-1-i]=b[i]-'0';
	}
	A[0]=A[0]+10;
	for(int i=1;i<a.size()-1;i++)
	{
		A[i]=A[i]+9;
	}
	A[a.size()-1]=A[a.size()-1]-1;
	for(int i=0;i<len;i++)
	{
		C[i]=A[i]-B[i];
	}
	for(int i=0;i<len;i++)
	{
		C[i+1]=C[i+1]+C[i]/10;
		C[i]=C[i]%10;
	}
	int k=len;
	while(C[k]==0)
	{
		k--;
	}
	
	for(int i=k;i>=0;i--)
	{
		stringstream tmp;
		string tmps;
		tmp<<C[i];
		tmp>>tmps;
		c=c+tmps;
	}
	return c;
}

string Mul(string a,string b)
{
	int A[200];
	int B[200];
	int C[200];
	string c="";
	memset(A,0,sizeof(A));
	memset(B,0,sizeof(B));
	memset(C,0,sizeof(C));
	int len=a.size()>b.size()?a.size():b.size();
	for(int i=0;i<a.size();i++)
	{
		A[a.size()-1-i]=a[i]-'0';
	}
	for(int i=0;i<b.size();i++)
	{
		B[b.size()-1-i]=b[i]-'0';
	}
	for(int j=0;j<b.size();j++)
	{
		for(int i=0;i<a.size();i++)
		{
			C[i+j]=C[i+j]+B[j]*A[i];
		}
	}
	for(int i=0;i<199;i++)
	{
		C[i+1]=C[i+1]+C[i]/10;
		C[i]=C[i]%10;
	}
	int k=199;
	while(C[k]==0)
	{
		k--;
	}
	for(int i=k;i>=0;i--)
	{
		stringstream tmp;
		string tmps;
		tmp<<C[i];
		tmp>>tmps;
		c=c+tmps;
	}
	return c;
}

string Div(string a,long long b)//a>b
{
	long long tmp=0;
	long long C[200];
	memset(C,0,sizeof(C));
	string c="";
	for(long long i=0;i<a.size();i++)
	{
		tmp=tmp*10+a[i]-'0';
		C[a.size()-1-i]=(long long)(tmp/b);
		tmp=tmp%b;
	}
	int k=199;
	while(C[k]==0)
	{
		k--;
	}
	for(int i=k;i>=0;i--)
	{
		stringstream tmp;
		string tmps;
		tmp<<C[i];
		tmp>>tmps;
		c=c+tmps;
	}
	return c;
}

int main()
{
	int s;
	cin>>s;
	while(s--)
	{
		string interger;
		cin>>interger;
		if(interger.size()>1)
		{
			string a,b;
			string tmp,tmp1=Sub(interger,"1");
			a=Div(Mul(interger,Sub(interger,"1")),2);
			tmp=Mul(interger,tmp1);
			tmp1=Sub(interger,"2");
			tmp=Mul(tmp,tmp1);
			tmp1=Sub(interger,"3");
			tmp=Mul(tmp,tmp1);
			b=Div(tmp,24);
			cout<<Add(Add(a,b),"1")<<endl;
		}
		else
		{
			switch(interger[0]-'0')
			{
			case 0:
				cout<<"1"<<endl;
				break;
			case 1:
				cout<<"1"<<endl;
				break;
			case 2:
				cout<<"2"<<endl;
				break;
			case 3:
				cout<<"4"<<endl;
				break;
			case 4:
				cout<<"8"<<endl;
				break;
			case 5:
				cout<<"16"<<endl;
				break;
			case 6:
				cout<<"31"<<endl;
				break;
			case 7:
				cout<<"57"<<endl;
				break;
			case 8:
				cout<<"99"<<endl;
				break;
			case 9:
				cout<<"163"<<endl;
				break;
			}
		}
	}

	return 0;
}