leetcode笔记：Dungeon Game

一. 题目描述

The demons had captured the princess (P) and imprisoned her in the bottom-right corner of a dungeon. The dungeon consists of M x N rooms laid out in a 2D grid. Our valiant knight (K) was initially positioned in the top-left room and must fight his way through the dungeon to rescue the princess.

The knight has an initial health point represented by a positive integer. If at any point his health point drops to 0 or below, he dies immediately.

Some of the rooms are guarded by demons, so the knight loses health (negative integers) upon entering these rooms; other rooms are either empty (0’s) or contain magic orbs that increase the knight’s health (positive integers).

In order to reach the princess as quickly as possible, the knight decides to move only rightward or downward in each step.

Write a function to determine the knight’s minimum initial health so that he is able to rescue the princess.

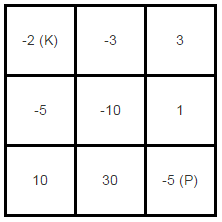
For example, given the dungeon below, the initial health of the knight must be at least 7 if he follows the optimal path RIGHT-> RIGHT -> DOWN -> DOWN.

Notes:

The knight’s health has no upper bound.
Any room can contain threats or power-ups, even the first room the knight enters and the bottom-right room where the princess is imprisoned.

二. 题目分析

题目很长，大致介绍了一款游戏的规则：

恶魔抓走了公主(P)并把她囚禁在地牢的右下角（矩阵图中的(P)所在的格子）。地牢包含M * N个房间。骑士(K)一开始位于左上角的格子里，目标是拯救公主。

骑士拥有初始生命值，为一正整数。如果在任何一个格子中，生命值变为0或小于0，他就会挂掉。

一些房间由恶魔守卫着，因此当骑士进入这些房间时就会损失生命值（负整数）；其他房间有两种，一种是空房间（数值为0），另外一种房间是存在一些魔力宝石，这些宝石可以增加骑士的生命值（正整数）。

为了尽快的解救到公主，骑士决定每一步只向右或者向下移动。

编写一个函数决定骑士的最小初始生命值，确保他可以成功营救公主。

题目给出一个例子，该例子中骑士的初始生命值至少应当为7，如果他按照下面的最优路线行进：右 -> 右 -> 下 -> 下.

该题目描述非常复杂，其实看懂规则后直接看例子比较容易理解，可使用动态规划来解决。令dungeon[i][j]表示从坐标(i, j)所在的格子出发，到最右下角公主所在处所需的最小血量。写出状态转换方程：

dungeon[i][j] = max(min(dungeon[i][j + 1], dungeon[i + 1][j]) - dungeon[i][j], 0)

三. 示例代码

class Solution {
public:
    int calculateMinimumHP(vector<vector<int> > &dungeon) {
        int m = dungeon.size();
        int n = dungeon[0].size();
        dungeon[m - 1][n - 1] = max(1 - dungeon[m - 1][n - 1], 1);
        // 边界值初始化
        for (int i = m - 2; i >= 0; --i) 
            dungeon[i][n - 1] = max(dungeon[i + 1][n - 1] - dungeon[i][n - 1], 1);

        for (int j = n - 2; j >= 0; --j) 
            dungeon[m - 1][j] = max(dungeon[m - 1][j + 1] - dungeon[m - 1][j], 1);

        for (int i = m - 2; i >= 0; --i) 
            for (int j = n - 2; j >= 0; --j) 
                dungeon[i][j] = max(min(dungeon[i][j + 1], dungeon[i + 1][j]) - dungeon[i][j], 1);

        return dungeon[0][0];
    }
};

四. 小结

该题有一定的难度，但如果能推出状态转换公式，使用动态规划可快速解决。