Leetcode题解14 84. Largest Rectangle in Histogram(hard)

Given n non-negative integers representing the histogram’s bar height where the width of each bar is 1, find the area of largest rectangle in the histogram.

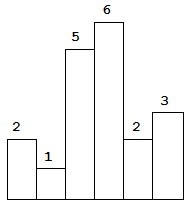
Above is a histogram where width of each bar is 1, given height = [2,1,5,6,2,3].

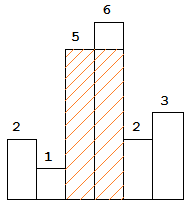
The largest rectangle is shown in the shaded area, which has area = 10 unit.

For example,
Given heights = [2,1,5,6,2,3],
return 10.

1、如果已知height数组是升序的，应该怎么做？

比如1,2,5,7,8

那么就是(1*5) vs. (2*4) vs. (5*3) vs. (7*2) vs. (8*1)

也就是max(height[i]*(size-i))

2、使用栈的目的就是构造这样的升序序列，按照以上方法求解。

但是height本身不一定是升序的，应该怎样构建栈？

比如2,1,5,6,2,3

（1）2进栈。s={2}, result = 0

（2）1比2小，不满足升序条件，因此将2弹出，并记录当前结果为2*1=2。

将2替换为1重新进栈。s={1,1}, result = 2

（3）5比1大，满足升序条件，进栈。s={1,1,5},result = 2

（4）6比5大，满足升序条件，进栈。s={1,1,5,6},result = 2

（5）2比6小，不满足升序条件，因此将6弹出，并记录当前结果为6*1=6。s={1,1,5},result = 6

2比5小，不满足升序条件，因此将5弹出，并记录当前结果为5*2=10（因为已经弹出的5,6是升序的）。s={1,1},result = 10

2比1大，将弹出的5,6替换为2重新进栈。s={1,1,2,2,2},result = 10

（6）3比2大，满足升序条件，进栈。s={1,1,2,2,2,3},result = 10

栈构建完成，满足升序条件，因此按照升序处理办法得到上述的max(height[i]*(size-i))=max{3*1, 2*2, 2*3, 2*4, 1*5, 1*6}=8<10

综上所述，result=10

public class Solution {
    public static int largestRectangleArea(int[] heights) {
        Stack<Integer> mStack = new Stack<Integer>();
        int count;
        int result = 0;
        for (int i = 0; i < heights.length; i++) {
            if (mStack.isEmpty() || mStack.peek() <= heights[i]) {
                mStack.push(heights[i]);
            } else {
                count = 1;
                while (!mStack.isEmpty() && mStack.peek() > heights[i]) {
                    result = max(result, mStack.peek() * count);
                    mStack.pop();
                    count++;
                }
                while (count > 1) {
                    mStack.push(heights[i]);
                    count--;
                }
                mStack.push(heights[i]);
            }
        }
        int num = 1;
        while (!mStack.isEmpty()) {
            result = max(result, mStack.pop() * num);
            num++;
        }
        return result;
    }

    public static int max(int i, int j) {
        return i >= j ? i : j;
    }
}