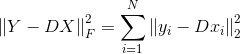K-SVD学习笔记
K-SVD是一个用于稀疏表示的字典学习算法，是一个迭代算法，是K-Means算法的泛化。
对于问题(1)
K-SVD的算法流程如下：
I)固定字典
，利用追踪算法(Pursuit Algorithm)求得(近似)最优的系数矩阵
；
II)每次更新一个列
(用SVD求解)，固定字典
及其相对应系数，使得问题(1)最小化；
III)重复I)、II)直至收敛。
接下来我们会详细的讨论K-SVD算法：
在稀疏编码阶段，固定字典，问题(1)的惩罚项可以重写为
那么问题(1)可以被分解为
个独立的问题
这个问题可以用OMP、BP、FOCUSS等追踪算法(Pursuit Algorithm)算法求解(这也体现了K-SVD算法的灵活性；FOCUSS能够得到更好地解，但OMP在保证比较好的解的同时，效率更高)，并且如果
足够小，我们就可以得到非常好的近似最优解。
第二阶段(更新字典的列)会稍微复杂一点，假设固定和，只关注字典的某一列及其相应的系数
(系数矩阵的第
行)，问题(1)的惩罚项可以重写为问题(2)
其中，假设
项是固定的，我们要更新的是第项，矩阵
表示除去第个字典项后的所有的个样本的误差。
也许有人会尝试利用SVD得到可选的和，尽管SVD能够有效的最小化上式误差，但是由于我们没有设置稀疏约束，所以新的向量会几乎被填满。
有一个简单直观的方法可以解决上面问题。
定义
存储用到字典项的样本索引，也就是的非零索引，即：
定义大小为
的矩阵
，矩阵元素
为1，其他矩阵元素均为0。
定义向量
(长度为
)，矩阵
(大小为
)，矩阵
(大小为)。
现在回到问题(2)，由于
有跟相同的支持度，所以问题(2)等价于问题(3)
现在可以直接用SVD解决问题(3)，得到
。最终我们得到
的第一列为
，
乘以
为
。
此解决方案必须满足两个条件：i)的列保持规范化；ii)所有表示的支持度保持不变或者变小。
字典列的更新与稀疏表示系数更新结合在一起加快了算法的收敛。
下图截自原论文，其中详细描述了K-SVD算法。
参考资料：K-SVD: An Algorithm for Designing Overcomplete Dictionaries for Sparse Representation