《机器学习系统设计》之数据理解和提炼

前言：

    本系列是在作者学习《机器学习系统设计》（[美] Willi Richert）过程中的思考与实践，全书通过Python从数据处理，到特征工程，再到模型选择，把机器学习解决问题的过程一一呈现。书中设计的源代码和数据集已上传到我的资源http://download.csdn.net/detail/solomon1558/8971649。

       第1章通过一个简单的例子介绍机器学习的基本概念，揭示过拟合的风险，帮助我们增强理解和提炼数据的能力。

1. 背景介绍

    假设互联网公司MLAAS为所有Web访问请求都提供服务，目前的服务器工作极限是每小时响应100 000个请求。我们希望利用历史数据预测何时达到基础设施的极限。

2. 数据读取和预处理

    现已收集到上个月的Web统计信息，并把它们汇集到web_traffic.tsv（以Tab字符分割数据，存在于配套资源中）。该数据集存储着每小时的访问次数，每一行包含连续的小时信息，以及该小时内的Web访问次数。文件前几行如下所示：

    通过快速检验显示，我们已经正确地读取各个列的数据，一共有743个二维点。将每个样本分成x，y两个列向量，这个切分过程通过SciPy的特殊索引标记来完成。

# coding=utf-8
# Chapter_1 Simple ML samplem
import scipy as sp
import matplotlib.pyplot as plt
# read data
data = sp.genfromtxt("data/web_traffic.tsv",delimiter="\t")
print(data[:10])
print(data.shape)

    为了清洗y向量中的无效值nan，使用布尔型数组来索引这个Scipy的数组。sp.isnan(y)返回一个布尔型数组，用来表示每个数组项中的内容是否是一个数字。使用~在逻辑上对数组取反，使得在x和y中只选择y值合法的项。

 

# clean data
x=data[:, 0]
y=data[:, 1]
print(sp.sum(sp.isnan(y)))
x=x[~sp.isnan(y)]
y=y[~sp.isnan(y)]

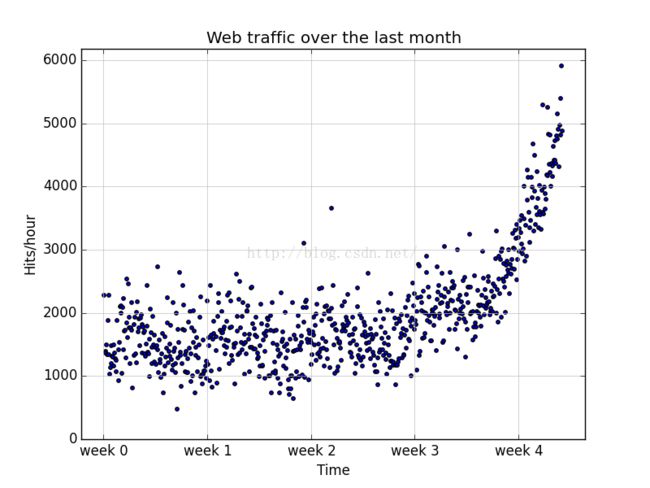
    为了获得对数据的总体印象，使用Matplotlib在散点图上将数据画出来。在图中可以看出前面几个星期的流量差不多相同，但是最后呢哥星期呈现出显著的上升趋势。

#draw pic
plt.scatter(x,y)
plt.title("Web traffic over the last month")
plt.xlabel("Time")
plt.ylabel("Hits/hour")
plt.xticks([w*7*24 for w in range(10)],['week %i'%w for w in range(10)])
plt.autoscale(tight=True)
plt.grid()
plt.show()

   

     为了方便绘制不同的模型，将绘图部分定义一个函数plot_models。

# all examples will have three classes in this file
colors = ['g', 'y', 'b', 'm', 'r']
linestyles = ['-', '-.', '--', ':', '-']
# plot input data
def plot_models(x, y, models, fname, mx=None, ymax=None, xmin=None):
    plt.clf()
    plt.scatter(x, y, s=10)
    plt.title("Web traffic over the last month")
    plt.xlabel("Time")
    plt.ylabel("Hits/hour")
    plt.xticks(
        [w * 7 * 24 for w in range(10)], ['week %i' % w for w in range(10)])
    if models:
        if mx is None:
            mx = sp.linspace(0, x[-1], 1000)
        for model, style, color in zip(models, linestyles, colors):
            # print "Model:",model
            # print "Coeffs:",model.coeffs
            plt.plot(mx, model(mx), linestyle=style, linewidth=3, c=color)
        plt.legend(["d=%i" % m.order for m in models], loc="upper left")
    plt.autoscale(tight=True)
    plt.ylim(ymin=0)
    if ymax:
        plt.ylim(ymax=ymax)
    if xmin:
        plt.xlim(xmin=xmin)
    plt.grid(True, linestyle='-', color='0.75')
    plt.savefig(fname)
    plt.show()

3. 选择正确的模型和学习算法

3.1 模型误差分析

    模型是对复杂现实世界的简化的理论近似，它总会包含一些近似误差。这个误差将指引我们在无数选择中寻找正确的模型。我们用模型预测值到真实值的平方距离计算这个误差。具体来说，对于一个训练好的模型函数f，按照下面的公式计算误差：

def error(f, x, y):
    return sp.sum((f(x) - y) ** 2)

3.2 模型选择

    先从最简单的直线模型开始，希望在散点图中找到一条最佳的直线，是结果中的近似误差最小。SciPy的polfit()函数正是用来解决这类问题的。给定数据x和y，以及期望的多项式的阶数（直线的阶是1），他可以找到一个模型，能够最小化之前定义的近似误差。

 

# create and plot models
fp1, res, rank, sv, rcond = sp.polyfit(x, y, 1, full=True)
print("Model parameters: %s" % fp1)
print("Error of the model:", res)
f1 = sp.poly1d(fp1)

     polyfit()函数会把拟合的模型函数所使用的参数返回，及fp1；通过把full置True，可以获得更多逼近过程的背景信息。得到的模型输出及残差（近似误差）如下：

Modelparameters: [   2.59619213  989.02487106]

('Errorof the model:', array([ 3.17389767e+08]))

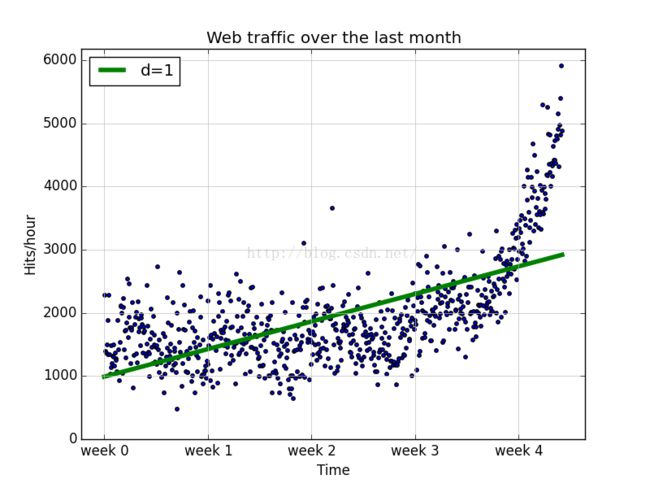
    然后用poly1d()根据这些参数创建一个模型函数，并画出第一个训练后的模型：

    从图中可以看出，该直线模型的输出与前四周的数据偏差较小，但是在第四周之后偏差较大，经计算实际误差值317389767.34。综上所述直线模型的拟合效果较差，可以把其作为模型比较的基线，直到找到更好的模型。

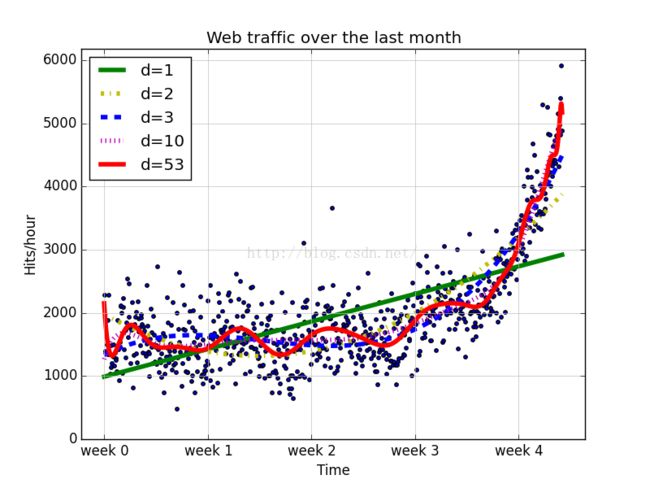
    接下来使用更高阶数：2,3,10,100来做拟合，看其是否可以更好地“理解”数据。

f2 = sp.poly1d(sp.polyfit(x, y, 2))
f3 = sp.poly1d(sp.polyfit(x, y, 3))
f10 = sp.poly1d(sp.polyfit(x, y, 10))
f100 = sp.poly1d(sp.polyfit(x, y, 100))
plot_models(x, y, [f1], os.path.join("..", "1400_01_02.png"))
plot_models(x, y, [f1, f2], os.path.join("..", "1400_01_03.png"))
plot_models(
    x, y, [f1, f2, f3, f10, f100], os.path.join("..", "1400_01_04.png"))

     

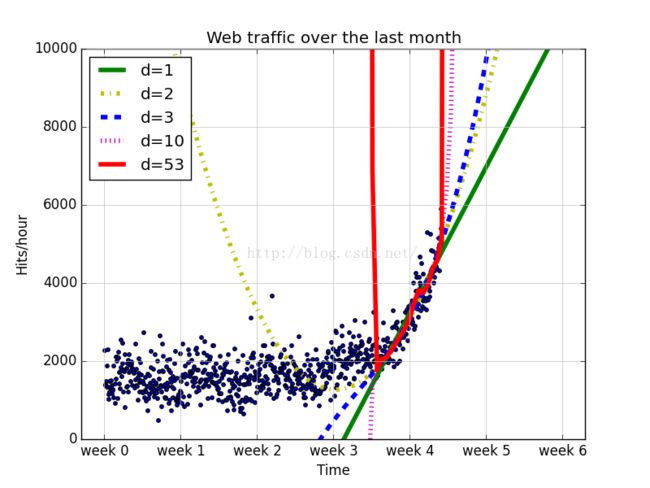
    模型越复杂，曲线对数据逼近的越好。它们的误差值也反映了同样的结果：

      Errors for the complete data set:

Errord=1: 317389767.339778

Errord=2: 179983507.878179

Errord=3: 139350144.031725

  Errord=10: 121942326.363551

    Errord=100: 109452403.015271

    然而，当阶数为10阶和100阶的多项式对数据的拟合出现了巨大的震荡。它不但捕捉到了背后的数据生成过程，还把噪音也包含了进去，这就叫做过拟合。

    在上述这5个拟合模型中，1阶模型太过简单，而10阶和100阶的模型显然过拟合了。而2阶和3阶模型在数据的两个边界上效果较差。我们还需要真正第理解数据。

    【注意】当运行程序时遇到了一个问题：阶数 d > 53时，plot出的图中显示d为53，与实际的阶数不符。

4. 模型改进

    从另一个角度重新分析数据，似乎在第3周到第4周的数据之间有一个拐点。折让我们可以以3.5周作为分界点把数据分成两份，并训练出两条直线来。我们使用第3之前的数据来训练第一条线，剩下的数据训练第2条线。

# fit and plot a model using the knowledge about inflection point
inflection = 3.5 * 7 * 24
xa = x[:inflection]
ya = y[:inflection]
xb = x[inflection:]
yb = y[inflection:]
fa = sp.poly1d(sp.polyfit(xa, ya, 1))
fb = sp.poly1d(sp.polyfit(xb, yb, 1))
plot_models(x, y, [fa, fb], os.path.join("..", "1400_01_05.png"))

    两条线组合起来似乎比之前的模型能更好地拟合数据，但组合之后的误差仍然高于高姐多项式的误差。我们最后能否相信这个误差呢？

    换一个方式来问，相比于其他复杂模型，为什么仅在最后一周数据上更相信拟合的直线模型？这是因为我们仍未它更符合未来的数据。如果在未来时间段上画出模型，就可以看到这是非常正确的。

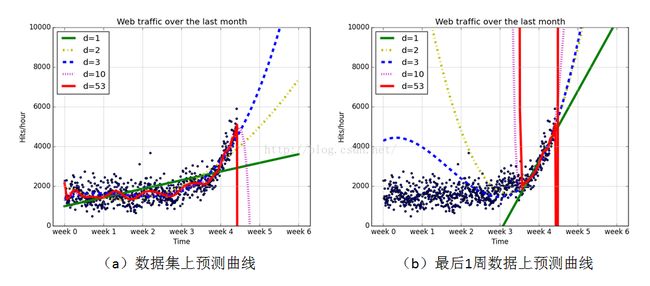
# extrapolating into the future
plot_models(
    x, y, [f1, f2, f3, f10, f100], os.path.join("..", "1400_01_06.png"),
    mx=sp.linspace(0 * 7 * 24, 6 * 7 * 24, 100),
    ymax=10000, xmin=0 * 7 * 24)
print("Trained only on data after inflection point")
fb1 = fb
fb2 = sp.poly1d(sp.polyfit(xb, yb, 2))
fb3 = sp.poly1d(sp.polyfit(xb, yb, 3))
fb10 = sp.poly1d(sp.polyfit(xb, yb, 10))
fb100 = sp.poly1d(sp.polyfit(xb, yb, 100))
print("Errors for only the time after inflection point")
for f in [fb1, fb2, fb3, fb10, fb100]:
    print("Error d=%i: %f" % (f.order, error(f, xb, yb)))
plot_models(
    x, y, [fb1, fb2, fb3, fb10, fb100], os.path.join("..", "1400_01_07.png"),
    mx=sp.linspace(0 * 7 * 24, 6 * 7 * 24, 100),
    ymax=10000, xmin=0 * 7 * 24)

    

    图（a）是各模型在全数据集上的预测曲线。10阶和100阶的模型非常努力地对给定数据正确建模，但它们无法推广到将来的数据上，及过拟合。另一方面，地阶模型则不能恰当地拟合数据，及欠拟合（underfitting）.

    如图（b）只拟合最后1周数据，因为我们相信最后1周的数据比之前的数据更符合未来的趋势。b图更加明显地显示出过拟合问题是如何不好。

    然而，当模型只在3.5周及以后数据上训练时，从模型误差中判断，仍然应该选择最复杂的那个模型。

                     Trainedonly on data after inflection point

                            Errorsfor only the time after inflection point

Errord=1: 22143941.107618

Errord=2: 19768846.989176

Errord=3: 19766452.361027

  Errord=10: 18949296.835986

    Errord=100: 18300735.896218

5. 训练与测试

    如果有一些未来数据用于模型评估，那么仅从近似误差结果中就应该可以判断出所选模型的优劣。如果没有未来数据，可以从现有数据中拿出一部分来模拟类似的结果。例如，把一定比例的数据删掉，并使用剩下的数据进行训练，然后在拿出的那部分数据上计算误差。

    只利用拐点时间后的数据训练出来的模型，其测试误差显现了一个完全不同的情况。

# separating training from testing data
frac = 0.3
split_idx = int(frac * len(xb))
shuffled = sp.random.permutation(list(range(len(xb))))
test = sorted(shuffled[:split_idx])
train = sorted(shuffled[split_idx:])
fbt1 = sp.poly1d(sp.polyfit(xb[train], yb[train], 1))
fbt2 = sp.poly1d(sp.polyfit(xb[train], yb[train], 2))
fbt3 = sp.poly1d(sp.polyfit(xb[train], yb[train], 3))
fbt10 = sp.poly1d(sp.polyfit(xb[train], yb[train], 10))
fbt100 = sp.poly1d(sp.polyfit(xb[train], yb[train], 100))
print("Test errors for only the time after inflection point")
for f in [fbt1, fbt2, fbt3, fbt10, fbt100]:
    print("Error d=%i: %f" % (f.order, error(f, xb[test], yb[test])))
plot_models(
    x, y, [fbt1, fbt2, fbt3, fbt10, fbt100], os.path.join("..",
                                                          "1400_01_08.png"),
    mx=sp.linspace(0 * 7 * 24, 6 * 7 * 24, 100),
    ymax=10000, xmin=0 * 7 * 24)

                                     

                                       Testerrors for only the time after inflection point

Errord=1: 8261798.132525

Errord=2: 7197691.673144

Errord=3: 7216384.013935

   Errord=10: 7564071.658053

   Errord=53: 7966754.023273

    综上所述，最优的模型是2阶模型，其测试误差最低，而这个误差是在模型训练中未使用的那部分数据上评估得到的。

6. 预测结果

     经过权衡利弊，我们已经得到了较优的模型。可以回答“服务器的响应请求何时到达每小时100 000次”。

    通过从多项式中减去100000，得到另一个多项式，然后计算出它的根。如果提供了参数的初始值，SciPy的optimize模块的fsolve函数可以完成这项工作。

from scipy.optimize import fsolve
print(fbt2)
print(fbt2 - 100000)
reached_max = fsolve(fbt2 - 100000, 800) / (7 * 24)
print("100,000 hits/hour expected at week %f" % reached_max[0])

输出结果如下：

       2

0.08609 x - 94.13 x + 2.749e+04

       2

0.08609 x - 94.13 x - 7.251e+04

100,000 hits/hour expected at week 9.613315

    模型告诉我们鉴于目前的用户行为和该公司的推进力，在第9周将会达到访问容量的界限。

7. 小结

    本文来源于《机器学习系统设计》第1章的内容，主要涉及了数据的读取与预处理、近似误差的计算、模型选择、过拟合的概念、训练/测试模型等内容。通过一个微小的机器学习示例来训练理解和提炼数据的能力，帮助我们将精力从算法转移到数据上来。