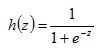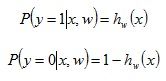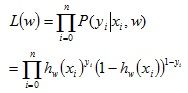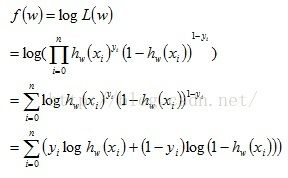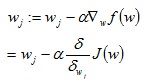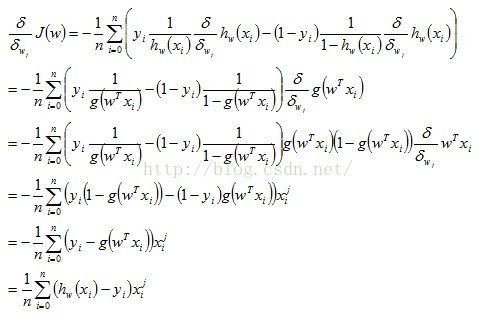Logistic Regression笔记
1.Logistic Regression模型
Logistic Regression预测的值是0和1，即Logistic Regression通过一系列函数作用后值域是{0，1}。那么，这个核心函数就是Sigmoid函数或Logistic函数。Sigmoid函数的表达形式如下：
函数图像如下：
Sigmoid函数的性质：当x=0时，Sigmoid(x)=0.5，并且，随着x的增大，Sigmoid函数的值逐渐趋近于1；而随着x的减小，Sigmoid函数的值逐渐趋近于0。如果横坐标足够大，那么Sigmoid函数看起来就像一个阶跃函数。
2.回归系数
为了实现Logistic回归分类器，我们可以在每个特征上都乘以一个回归系数，然后把所有的结果值相加，将这个总和代入Sigmoid函数中，进而得到一个范围在0~1之间的数值。任何大于0.5的数据被分入1类，小于0.5的数据被分入0类。所以，Logistic回归也可以被看做是一种概率估计。现在假设有n个训练样本
，其相应的类型标签是
，而对应的权值即系数不妨设为
，则求出z值：
上式采用向量写法，可以表示成 
。其中的向量x是分类器的输入数据，向量w也就我们要找的最佳系数，从而使得分类器尽可能地精确。
3.确定回归系数
在前两节，我们都提到Logistic Regression模型的一个重要性质：当z无穷大时，h(z)趋近于1；当z无穷小是，h(z)趋近于0；当z=0时，h(z)=0.5。我们构造预测函数：
同时，前面我们也提到过：Logistic回归也可以被看成是一种概率估计。那么我们不妨用h(z)表示结果取1的概率，因此，可以得到1类和0类的概率公式，如：
以下使用极大似然估计法来求解回归系数。参数w的似然函数是：
由于往往极大似然函数求解比较难，所以一般会对极大似然函数取对数。因此得到下式：
实际上，代价函数（cost function）的形式是：
所以，求最小化代价函数就等价于求最大化似然估计，也就求出了回归系数。
这里用梯度下降法来求解f(w)的的极大值，即
对f(w)求导得：
代入原式可得到：
其中
表示第i个样本的第j个特征。
4.伪代码
梯度下降法的伪代码：每个回归系数初始化为1
重复R次：
计算整个数据集的梯度
使用alpha*gradient更新回归系数的向量
返回回归系数
参考文献：
http://blog.csdn.net/pakko/article/details/37878837
http://www.cnblogs.com/guyj/p/3800519.html