java 实现后缀数组及最长回文子串问题
摘要: 后缀数组的java实现。 利用后缀数组来求解最长回文子串问题。
关键词: 后缀数组, 倍增算法, 基数排序,height[]数组,最长回文子串
参考文献:《后缀数组_处理字符串的有效工具》。
part I . 后缀数组中一些相关定义
Suffix(i)表示以i开始的后缀, 对于字符串"aabaaaab"来说,Suffix(2)=baaaab
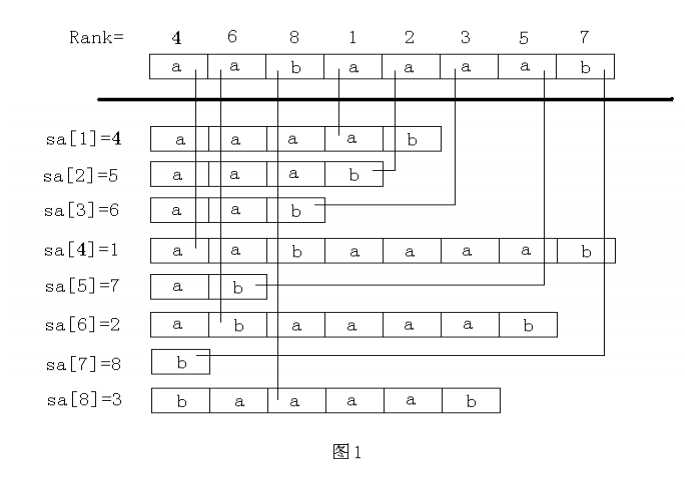
Rank[i] 表示以Suffix(i) 在所有的后缀 的rank.
Sa[i] 表示排名第i的后缀的下标。
参照图1,很容易理解Rank[] 和Sa[]。
Rank[] 与 Sa[] 有简单的置换关系:
Rank[S[i]] = i;
S[Rank[i]] = i;
求出一个来可以很容易的获得另外一个。
接下来的问题,怎么样求出后缀数组?罗大牛在论文中提到两种算法倍增算法和DC3算法。
倍增算法的思路如下:
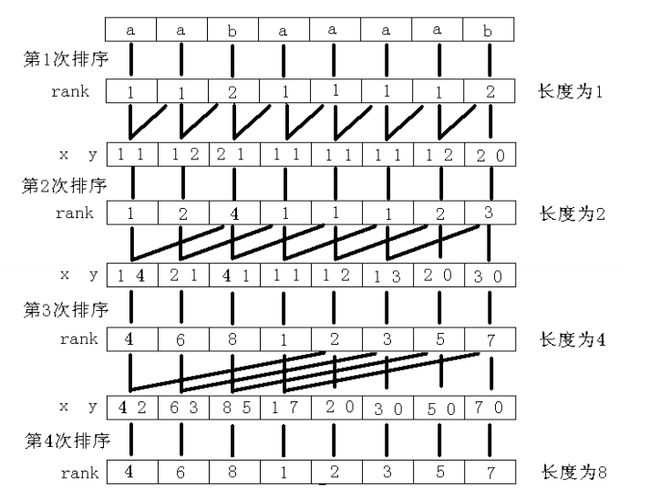
第 i 次 倍增时,对以 j 开始的长度为2^i的子串进行排序。利用第 i -1 次 倍增后的结果。
长度为2^i的子串可以表示成2个长度为2^(i-1)的子串的rank,即有两个关键字。然后进行基数排序。
如下图所示,可以很简单的理解。有时候图片比文字的表达能力强大很多。
罗大牛的c语言模板写的相当简洁,不过对于一个java程序员来说,搞清楚那四个数组的含义,还有其中用到的运算技巧真是很痛苦。等哪天心情好了,再看。
一副图片其实就把后缀数组的含义解释的很清楚了。
算法复杂度: 总共需要O(logn)次倍增,每一次倍增进行基数排序需要两次分配和收集,复杂度O(2*n), 总复杂度O(nlogn).
part II . height[]数组
height[]数组的含义:height[i]表示排序为 i 的后缀与排序为 i-1 的后缀的最长公共前缀的长度。
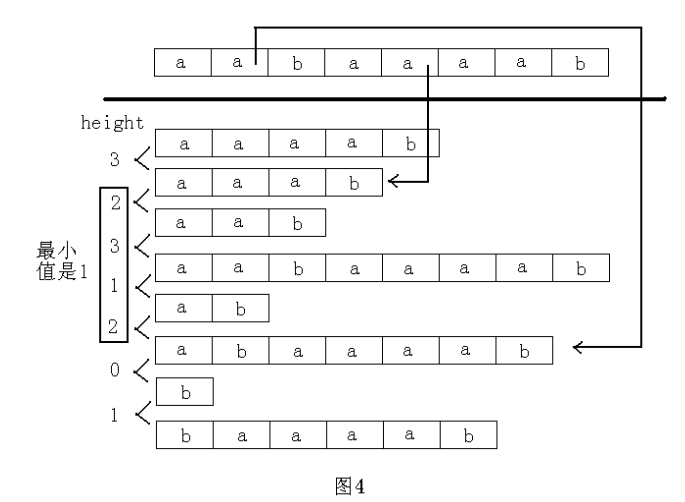
还是看图:
假设rank[i] < rank[j], 任意两个后缀 i 和 j 的最长公共前缀的长度, 是height[rank[i]+1], height[rank[i]+2]...height[rank[j]]的最小值。
如图4所示,suffix(4)=aaab 与 suffix(1)=abaaaab的最长公共前缀的长度为1。
怎么计算height[]数组。
最简单的想法是,计算排序相邻的两个后缀的公共前缀。
for(int i = 1;i<n;i++){
int j = sa[i];
int k = sa[i-1];
height[i] = 0;
while(str[j+height[i]]==str[k+height[i]]) height[i]++;
}
上面几行代码看做伪代码吧,没有考虑太多细节。 最坏的情况:str="aaaaaaaa", suffix(sa[0]) =" a", suffix(sa[1]) ="aa", suffix(sa[2])="aaa",suffix(sa[3])="aaaa" .....
这样最多需要1+2+3+...+n-1次比较,O(n^2)的算法。
怎么样去优化? 可以利用某些性质,使得height[i] 不是每次都从0开始。
对于图4中的例子,suffix(4) ="aaab" , suffix(5)="aab", sa[1] = 4, rank[4] = 1 , sa[2] =5, rank[5] =2 , suffix(4)在suffix(5)的前面,height[rank[5]] =height[2] = 2, 那么suffix(4)和suffix(5)各自向后移动一个,变成aab=suffix(5)和ab=suffix(6),那么aab也在ab的前面, 因此,对于ab来说,其height[rank[6]]的长度至少为height[rank[5]]-1=1. 仔细观察图4,suffix(sa[2])=aab,suffix(sa[4])=ab,此外,
suffix(sa[3]) = aabaaaab. 因此在计算ab的height时,在与suffix(sa(rank[6]-1))进行比较时,不需要再从0开始进行匹配。
令h[i] 表示height[rank[i]],则h[i-1]=height[rank[i-1]]
h[]数组的重要性质:h[i]>=h[i-1]-1
part III . 最长回文子串
计算最长回文子串,怎么利用后缀数组解决?
最长回文子串可以转换成求两个后缀的最长公共前缀。
令S="aabaaaab", 构造SS'="aabaaab$baaabaa",其长度为len ,那么求以S中以i为中心的最长回文子串,根据回文串的性质,就变成在SS'中求suffix(i)和suffix(len-i)的最长公共前缀的问题。
另外需要做一些长度为奇数偶数的处理。主要思路是关键。
源码分析如下:
public interface Buckable{
/**第i次基数排序时映射到哪个桶里*/
public int map(int pass);
}
import java.util.Arrays;
public class Bucket {
/**桶,只用来进行计数*/
private int[] buckets;
/**桶的个数,最多需要多少个*/
private int bucketNum;
/**总共需要多少次排序,也就是基数排序时,多关键字的位数*/
private int passes;
public Bucket(int m,int n){
this.bucketNum = m;
this.buckets = new int[m];
this.passes = n;
}
public int[] sort(Buckable[]data){
/**order表示data的进入桶的顺序*/
int[] order = new int[data.length];
for(int i = 0;i<order.length;i++){
order[i] = i;
}
return sort(data,order);
}
/**
*order表示data的进入桶的顺序, 排序完需要重新设置order,
*设置data在下一轮进入桶时的顺序。
*/
public int[] sort(Buckable[]data,int[] order){
for(int i = 0;i<this.passes;i++){
sort(data,order,i);
}
/** data的rank值,从1开始,data相同的话,其rank也相同*/
int[] rank = new int[data.length];
rank[order[0]] = 1;
for(int i = 1;i<order.length;i++){
if(data[order[i]].equals(data[order[i-1]])){
rank[order[i]] = rank[order[i-1]];
}else{
rank[order[i]] = rank[order[i-1]]+1;
}
}
return rank;
}
public void sort(Buckable[] data,int[] order,int pass){
if(data.length!=order.length || pass<0){
throw new IllegalArgumentException();
}
//map the data to the bucket no.
int[] bucketNo = new int[data.length];
for(int i = 0;i<data.length;i++){
bucketNo[i] = data[i].map(pass);
}
Arrays.fill(this.buckets, 0);
//put into bucket
for(int i = 0;i<order.length;i++){
int or = order[i];
int bu = bucketNo[or];
this.buckets[bu]++;
}
for(int i = 1;i<this.bucketNum;i++){
this.buckets[i] += this.buckets[i-1];
}
/**新的order的计算要从后面开始计算,因为一个桶中,进入桶中比较晚的元素,其order也比较大*/
int[] newOrder = new int[order.length];
for(int i = order.length-1;i>=0;i--){
newOrder[this.buckets[bucketNo[order[i]]]-1] = order[i];
this.buckets[bucketNo[order[i]]]--;
}
for(int i = 0;i<order.length;i++){
order[i] = newOrder[i];
}
}
}
/**倍增算法中每个元素的键值,由两个数组成*/
public class DAPair implements Buckable{
private int rank[]= new int[2];
public DAPair(int r0,int r1){
this.rank[0] = r0;
this.rank[1] = r1;
}
@Override
public int map(int pass) {
if(pass>=2 || pass <0){
throw new IllegalArgumentException();
}
if(pass==0){
return this.rank[1];
}
return this.rank[0];
}
@Override
public boolean equals(Object o){
if(o instanceof DAPair){
return this.rank[0] == ((DAPair)o).rank[0] &&
this.rank[1] == ((DAPair)o).rank[1];
}
return false;
}
}
public class SuffixArray {
private String string;
//记录下表为i的后缀的排序
private int rank[];
//记录排序为i的后缀的下标
private int sa[];
private int height[];
public SuffixArray(String string){
if(string==null) throw new NullPointerException();
this.string = string;
this.rank = new int[string.length()];
this.sa = new int[string.length()];
this.height = new int[string.length()];
build();
}
private DAPair[] fromArray(int[] a,int inc){
DAPair[] pairs = new DAPair[a.length];
for(int i = 0;i+inc<a.length;i++){
pairs[i] = new DAPair(a[i],a[i+inc]);
}
for(int i = a.length-inc;i<a.length;i++){
pairs[i] = new DAPair(a[i],0);
}
return pairs;
}
private void build(){
if(this.string.isEmpty()==false){
//build suffix array
int len = string.length();
class LowcaseCharacter implements Buckable{
private char ch;
public LowcaseCharacter(char c){
this.ch = c;
}
@Override
public int map(int pass) {
if(pass!=0) throw new IllegalArgumentException();
return ch;
}
@Override
public boolean equals(Object o){
if(o instanceof LowcaseCharacter){
return ((LowcaseCharacter) o).ch==this.ch;
}
return false;
}
}
Buckable[] buckables = new Buckable[len];
for(int i=0;i<len;i++){
buckables[i] = new LowcaseCharacter(string.charAt(i));
}
Bucket bucket = new Bucket(130,1);
this.rank = bucket.sort(buckables);
bucket = new Bucket(this.string.length()+2,2);
//倍增算法
for(int i = 1;i<len;i=i<<1){
DAPair[] dapairs = fromArray(this.rank,i);
for(int j = 0;j<this.sa.length;j++){
this.sa[j] = j;
}
this.rank = bucket.sort(dapairs,this.sa);
}
for(int i = 0;i<this.rank.length;i++){
this.rank[i]--;
}
//build height array
int k = 0;
for(int i=0;i<this.sa.length;i++){
if(k>0) k--;
if(rank[i]==0) continue;
int j = this.sa[rank[i]-1];
for(;i+k<this.string.length() &&
j+k<this.string.length() &&
this.string.charAt(i+k)==this.string.charAt(j+k);
k++);
height[rank[i]] = k;
}
}
}
//Suffix(id1)和Suffix(id2)的最长公共前缀的长度
public int getLCP(int id1,int id2){
if(id1==id2) return this.string.length()-id1+1;
int r1 = this.rank[id1];
int r2 = this.rank[id2];
int minr = r1<r2?r1:r2;
int maxr = r1>r2?r1:r2;
int lcp = this.string.length();
for(int i = minr+1;i<=maxr;i++){
if(lcp>this.height[i]){
lcp = this.height[i];
}
}
return lcp;
}
public int[] getRank(){
return this.rank;
}
public int[] getSuffixArray(){
return this.sa;
}
//最长回文子串
public String getLP(){
StringBuffer buffer = new StringBuffer(this.string.length()*2+2);
for(int i = 0;i<this.string.length();i++){
buffer.append("#"+this.string.charAt(i));
}
buffer.append("#$");
for(int i = this.string.length()-1;i>=0;i--){
buffer.append("#"+this.string.charAt(i));
}
buffer.append("#");
String newStr = buffer.toString();
SuffixArray sa = new SuffixArray(newStr);
int maxLcp = -1;
int id = -1;
for(int i = 1;i<newStr.length()/2;i++){
int lcp = sa.getLCP(i, newStr.length()-i-1);
if(maxLcp<lcp) {
maxLcp = lcp;
id = i;
}
}
String rs = newStr.substring(id-maxLcp+1,id+maxLcp);
rs = rs.replaceAll("#", "");
return rs;
}
public static void main(String[]args){
String s = "ababababa";
SuffixArray sa = new SuffixArray(s);
System.out.println(sa.getLP());
}
}