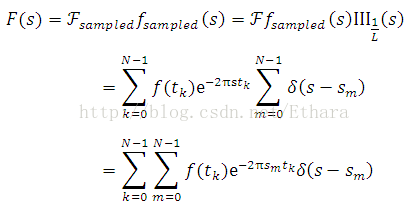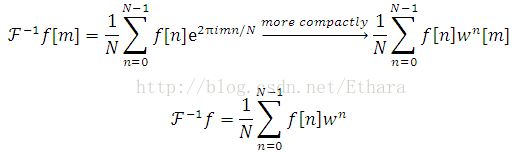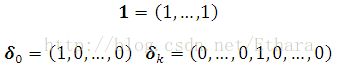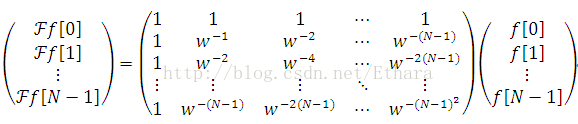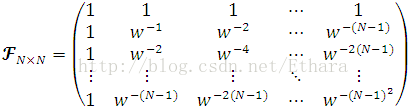Discrete Fourier Transform
Discrete Fourier Transform
Ethara
Particularly in the modern world, it is the discrete Fourier transform (DFT) that is highly utilized to analyze the spectrum of a signal in the frequency domain. Rather than presenting the definition of DFT directly, this work will go through the derivation of DFT by moving from the continuous and analog to the discrete and digital.
Suppose f(t) is a continuous signal. Here comes the outline of this work,
1). Find a reasonable discrete approximation to f(t).
2). Find a reasonable discrete approximation to the Fourier transform of f(t).
3). Find a reasonable way of passing discrete form of f(t) to discrete form of its Fourier transform.
4). Derive some nice properties of DFT.
We first digress to the sampling theorem before going through DFT. The sampling theorem says,
Given a sequence of discrete signals indexed by time, the original continuous signal f(t) can be perfectly reconstructed as
if and only if the Nyquist condition is satisfied,
where p/2 is called the cut-off frequency.
This indicates that points k/p’s are the sample points spaced 1/p apart. Therefore, to reconstruct f(t) without any errors, we need to sample from the original continuous signal f(t) at the sampling rate equal or higher than p,which is also called the “Nyquist rate”.
Furthermore, we can put it into a more generous context, that is, how rapidly to sample in one domain depends upon the range of the domain, explicitly in the form of reciprocity relationship (*).
Now let’s get to the derivation on DFT with the following assumptions,
However, these two assumptions cannot hold simultaneously. But we will see that it is satisfactory to play along with the misapplied version of sampling theorem.
First, we can get a reasonable discrete approximation of f(t) by taking N samples spaced 1/2B apart (See (*)). Thus, we have, N(1/2B) = L, i.e., N = 2BL, and the samples at
Now we can obtain the sampled form of f(t) by multiplying Shah function,
Since f(t) is limited to [0, L],
Taking Fourier transform (1) of this,
Then, we will sample (1) in the frequency domain by taking M samples spaced 1/L (See(*)) in the range [0, 2B]. M(1/L)= 2B yields M = 2BL = N. The M(= N) samples are
Likewise, the sampled form of (1) is
Since the Fourier transform of f(t) is limited to [0, L],
Therefore, the sampled values (2) of the Fourier transform of f(t),
which is the discrete approximation of Fourier transform of discrete approximation of f(t).
In general,
where
Moreover, to eliminate the continuous and use only discrete signals, noting that tk = k/2B, sm = m/L, tksm = km/N, and identifying f(tk) with value f[k] of discrete signal f = (f[0], …, f[N-1]) and the Fourier transform evaluated at sk with value F[k] of discrete signal F= (F[0], …, F[N-1]), we obtain the DFT with all traces of continuous variables gone,
Resolution Independence
Suppose deltat and deltas denote the resolution in time and frequency respectively, as in the figure below.
Noting that,
we can obtain the independence that resolution in one domain is fixed by choices in the other domain due to this reciprocity relationship.
Vector Complex Exponentials
Here we define the vector complex exponential,
Taking the m’th component of w,
Taking powers of w,
With the vector complex exponentials, we can rewrite DFT as
or more compactly,
Taking the inner product between wk and wl,
we see that the vector complex exponentials are orthogonal but not quite orthonormal.
Without derivations (“I don’t like it when you write down the formula and say ‘Son of bitch, it works’, but I am gonna do it anyway.”), we present the inverse DFT as,
Noticeably, there are two special discrete signals,
Using the definition of DFT, we can easily obtain,
Now, by redefining w is the N’th root of 1, i.e.,
![]()
we will have a different perspective on the definition of DFT, that is, we can view DFT as an N-by-N matrix and computing DFT as matrix multiplication. Noting that, the m’th component of DFT can be rewritten as,
Therefore,
Let Matrix (2)
where, in a more mnemonic way,
![]()
Moreover, noting that,
![]()
Matrix(2) is symmetric but not quite unitary.
Furthermore,
This is another way of getting the inverse DFT.
Due to the periodicity forced onto DFT, we can write, by putting f[0] in the middle of spectrum,
Finally, we introduce the reversed signal
![]()
and formulate the DFT duality,