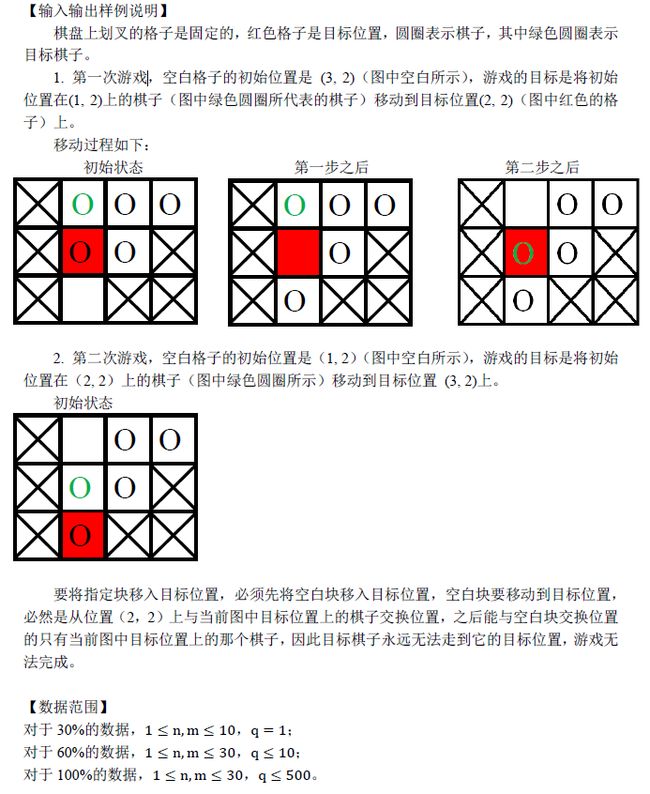
JZOJ 3537【NOIP2013提高组day2】华容道

Description

小 B 最近迷上了华容道，可是他总是要花很长的时间才能完成一次。于是，他想到用编程来完成华容道：给定一种局面，华容道是否根本就无法完成，如果能完成，最少需要多少时间。
小 B 玩的华容道与经典的华容道游戏略有不同，游戏规则是这样的：
在一个 n*m 棋盘上有 n*m 个格子，其中有且只有一个格子是空白的，其余 n*m-1个格子上每个格子上有一个棋子，每个棋子的大小都是 1*1 的；
有些棋子是固定的，有些棋子则是可以移动的；
任何与空白的格子相邻（有公共的边）的格子上的棋子都可以移动到空白格子上。 游戏的目的是把某个指定位置可以活动的棋子移动到目标位置。
给定一个棋盘，游戏可以玩 q 次，当然，每次棋盘上固定的格子是不会变的，但是棋盘上空白的格子的初始位置、指定的可移动的棋子的初始位置和目标位置却可能不同。第 i 次玩的时候，空白的格子在第 EX_i 行第 EY_i 列，指定的可移动棋子的初始位置为第 SX_i 行第 SY_i 列，目标位置为第 TX_i 行第 TY_i 列。
假设小 B 每秒钟能进行一次移动棋子的操作，而其他操作的时间都可以忽略不计。请你告诉小 B 每一次游戏所需要的最少时间，或者告诉他不可能完成游戏。

Analysis

这题是NOIP的压轴题。
为了方便后文说明，规定空白格子为白块，初始位置上的棋子叫特殊块（其余棋子都是一样的）。
首先，有一个很显然的结论：移动棋子等价于移动白块。
又因为其余棋子都是等价的，所以记录移动中白块和特殊块的位置就能确定一个局面。
这样，用宽搜可以通过70%的数据点（如果你RP好可以过80%）。
但是对于100%的数据这样的方法想不到优化，看来要另寻别径了。
其实上面的状态表示还可以优化：注意到对于特殊块的位置只有在与白块交换时会改变，所以我们只用记录 f[x][y][fx] ，表示特殊块的坐标以及一个方位（上下左右），表示白块在特殊块的这个方位。
这样，为了模拟特殊块移动，我们还要预处理出一个值： f[x][y][fx]−>f[x][y][fx′] ，这一步相当于改变运动方向。另外，通过交换白块和特殊块就相当于走一步。
某Bigzao发问：那对于特殊块与白块不相邻的移动，没有实现啊。
请注意：改变方向其实也会产生不相邻的移动，所以实现在预处理里面。
这样，把块抽象成点，就能用最短路实现最短移动距离。
所以对于每个询问，一开始暴力把白块移到特殊块的四个方位，然后按照上述连边。再跑一遍最短路，就能解决问题了。 O(n2∗m2∗16+q∗n∗m)

Code

#include<cstdio>
#include<queue>
#include<cstring>
#include<algorithm>
#define fo(i,a,b) for(int i=a;i<=b;i++)
#define num(i,j) ((i-1)*m+(j))
#define F(i,j,k) (k+4*(num(i,j)-1))
using namespace std;
const int N=35,M=905,V=M*4,E=V*5,INF=2139062143,
fx[4][2]={{-1,0},{1,0},{0,-1},{0,1}};
int n,m,S,q1[M*M][2],q2[M*M][2],data[M*M],c[M][4][4];
int tot,to[E],next[E],wei[E],last[V],dis[V];
bool map[N][N],bz[N][N],bz1[V],p[V];
queue<int> q;
int bfs(int xs,int ys,int xt,int yt,int x0,int y0)
{
    if(xs==xt && ys==yt) return 0;
    q1[1][0]=xs,q1[1][1]=ys;
    data[1]=0;
    memset(bz,0,sizeof(bz));
    bz[xs][ys]=1;
    int l=0,r=1;
    while(l<r)
    {
        int x=q1[++l][0],y=q1[l][1];
        fo(i,0,3)
        {
            int xx=x+fx[i][0],yy=y+fx[i][1];
            if(!map[xx][yy] || bz[xx][yy]) continue;
            if(xx==x0 && yy==y0) continue;
            data[++r]=data[l]+1;
            if(xx==xt && yy==yt) return data[r];
            q1[r][0]=xx,q1[r][1]=yy;
            bz[xx][yy]=1;
        }
    }
    return -1;
}
void link(int u,int v,int w)
{
    to[++tot]=v;
    wei[tot]=w;
    next[tot]=last[u];
    last[u]=tot;
    if(tot&1) link(v,u,w);
}
void SPFA()
{
    memset(dis,127,sizeof(dis));
    memset(bz1,0,sizeof(bz1));
    dis[S]=0;
    bz1[S]=1;
    q.push(S);
    while(!q.empty())
    {
        int u=q.front();q.pop();
        for(int i=last[u];i;i=next[i])
        {
            int v=to[i];
            if(dis[u]+wei[i]<dis[v])
            {
                dis[v]=dis[u]+wei[i];
                if(!bz1[v])
                {
                    q.push(v);
                    bz1[v]=1;
                }
            }
        }
        bz1[u]=0;
    }
}
int main()
{
    int _,x0,y0,xs,ys,xt,yt;
    scanf("%d %d %d",&n,&m,&_);
    fo(i,1,n)
        fo(j,1,m) scanf("%d",&map[i][j]);
    fo(i,1,n)
        fo(j,1,m)
            fo(k,0,3)
            {
                int i1=i+fx[k][0],j1=j+fx[k][1];
                if(!map[i1][j1]) continue;
                fo(l,0,3)
                    if(k!=l)
                    {
                        int i2=i+fx[l][0],j2=j+fx[l][1];
                        if(!map[i2][j2]) continue;
                        c[num(i,j)][k][l]=bfs(i1,j1,i2,j2,i,j);
                    }
            }
    S=0;
    while(_--)
    {
        scanf("%d %d %d %d %d %d",&x0,&y0,&xs,&ys,&xt,&yt);
        if(xs==xt && ys==yt)
        {
            printf("0\n");
            continue;
        }
        tot=0;
        memset(last,0,sizeof(last));
        memset(p,0,sizeof(p));
        fo(i,0,3)
        {
            int x=xs+fx[i][0],y=ys+fx[i][1];
            if(!map[x][y]) continue;
            int w=bfs(x0,y0,x,y,xs,ys);
            if(w!=-1) link(S,F(xs,ys,i),w);
            p[F(xs,ys,i)]=1;
        }
        fo(i,1,n)
            fo(j,1,m)
                fo(k,0,3)
                {
                    int i1=i+fx[k][0],j1=j+fx[k][1];
                    if(!map[i1][j1]) continue;
                    link(F(i,j,k),F(i1,j1,k^1),1);
                    p[F(i,j,k)]=p[F(i1,j1,k^1)]=1;
                    fo(l,0,3)
                    if(k!=l)
                    {
                        int i2=i+fx[l][0],j2=j+fx[l][1];
                        if(!map[i2][j2]) continue;
                        if(c[num(i,j)][k][l]!=-1) link(F(i,j,k),F(i,j,l),c[num(i,j)][k][l]);

                        p[F(i,j,k)]=p[F(i,j,l)]=1;

                    }
                }
        SPFA();
        int ans=INF;
        fo(i,0,3)
            if(p[F(xt,yt,i)]) ans=min(ans,dis[F(xt,yt,i)]);
        printf("%d\n",ans==INF?-1:ans);
    }
    return 0;
}