Gibbs sampling & R

Gibbs sampling & R

分类： R 统计计算statistical computing 抽样、模拟、实验设计 2011-12-13 21:28  404人阅读  评论(0)  收藏  举报

维基百科的定义：http://en.wikipedia.org/wiki/Gibbs_sampling

我们假设一个随机的二元变量(x,y)，然后计算其中一个或全部的边缘分布p(x),p(y)。这种抽样思想是考虑条件分布p(xly),p(ylx)，比通过联合密度
p(xy)来计算求解简单,例如

首先，我们要进行初始化y0，然后通过条件概率P(xIy=y0)计算得出x0,然后再基于x0的条件分布p(ylx=x0)提取出一个更新后的y1。样本的更新过程是这样的:

,

重复该过程，可以生成一个GIBBS序列，其算法可抽象为：

例如：模拟一个(x,y)二元正态分布，该分布的一个边际分布为标准正态分布x~N(0,1)，x,y间的相关系数记为r。

我们利用Gibbs抽样进行模拟：

 gibbs<-function (n, r)
 {
         mat <- matrix(ncol = 2, nrow = n)
         x <- 0
         y <- 0
         mat[1, ] <- c(x, y)
         for (i in 2:n) {
                 x <- rnorm(1, r * y, sqrt(1 - r^2))
                 y <- rnorm(1, r * x, sqrt(1 - r^2))
                 mat[i, ] <- c(x, y)
         }
         mat
 }
 bvn<-gibbs(10000,0.98)

当然这个例子也可以直接模拟服从标准正态分布的边际分布x,再利用条件分布y|x进行模拟

 rbvn<-function (n, r)
 {
         x <- rnorm(n, 0, 1)
         y <- rnorm(n, r * x, sqrt(1 - rho^2))
         cbind(x, y)
 }
 bvn<-rbvn(10000,0.98)

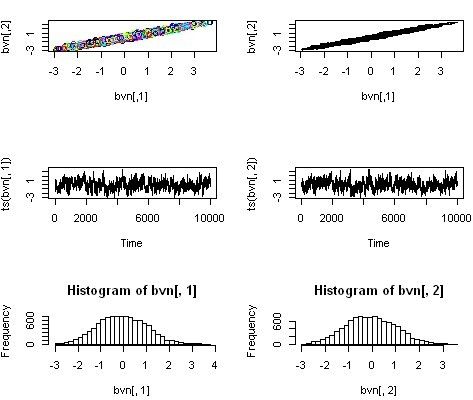
可以通过作图来看看两种模拟的效果

 par(mfrow=c(3,2))
 plot(bvn,col=1:10000)
 plot(bvn,type="l")
 plot(ts(bvn[,1]))
 plot(ts(bvn[,2]))
 hist(bvn[,1],40)
 hist(bvn[,2],40)
 par(mfrow=c(1,1))

结果如图

 

资料来源：

《基于网络的可适应Gibbs抽样方法研究》

http://www.mas.ncl.ac.uk/~ndjw1/teaching/sim/gibbs/gibbs.html

 

更多例子：

a.demo for one-way random effects model.

http://www.stat.sc.edu/~grego/courses/stat740/gibbs.1wayre.txt

b.simple Gibbs sampler class demonstration.

http://www.stat.sc.edu/~grego/courses/stat740/NWK1732.txt

 

更多资源：

《Introduction to Probability Simulation and Gibbs Sampling With R》

《Bayesian Computation With R》

《Introducing Monte Carlo Methods with R (Use R)》