【NOIP2015】运输计划 差分数组+线段树+树链剖分
最开始考NOIP的时候看到这个题目写了个SPFA,写搓了一分都没有,后来学了不少新姿势以后重新想起了这个题目据说倍增可以水60分,额,想了一想不知道怎么弄,于是我就开始写可以A的算法了,别人告诉我这个题目会被卡常数,有点慌![]()
![]()
好吧后来除了二分边界错了并没有被卡常数,可能是因为我最开始就注意压缩常数了吧。
BZOJ:http://www.lydsy.com/JudgeOnline/problem.php?id=4326
CODEVS:http://codevs.cn/problem/4632/
题目描述 Description
公元 2044 年,人类进入了宇宙纪元。L 国有 n 个星球,还有 n−1 条双向航道,每条航道建立在两个星球之间,这 n−1 条航道连通了 L 国的所有星球。小 P 掌管一家物流公司, 该公司有很多个运输计划,每个运输计划形如:有一艘物流飞船需要从 ui 号星球沿最快的宇航路径飞行到 vi 号星球去。显然,飞船驶过一条航道是需要时间的,对于航道 j,任意飞船驶过它所花费的时间为 tj,并且任意两艘飞船之间不会产生任何干扰。为了鼓励科技创新, L 国国王同意小 P 的物流公司参与 L 国的航道建设,即允许小P 把某一条航道改造成虫洞,飞船驶过虫洞不消耗时间。在虫洞的建设完成前小 P 的物流公司就预接了 m 个运输计划。在虫洞建设完成后,这 m 个运输计划会同时开始,所有飞船一起出发。当这 m 个运输计划都完成时,小 P 的物流公司的阶段性工作就完成了。如果小 P 可以自由选择将哪一条航道改造成虫洞, 试求出小 P 的物流公司完成阶段性工作所需要的最短时间是多少?
输入描述 Input Description
第一行包括两个正整数 n,m,表示 L 国中星球的数量及小 P 公司预接的运输计划的数量,星球从 1 到 n 编号。接下来 n−1 行描述航道的建设情况,其中第 i 行包含三个整数 ai,bi 和 ti,表示第 i 条双向航道修建在 ai 与 bi 两个星球之间,任意飞船驶过它所花费的时间为 ti。数据保证 1<=ai,bi<=n 且 0<=ti<=1000。接下来 m 行描述运输计划的情况,其中第 j 行包含两个正整数 uj 和 vj,表示第 j 个运输计划是从 uj 号星球飞往 vj号星球。数据保证 1<=ui,vi<=n
输出描述 Output Description
输出文件只包含一个整数,表示小 P 的物流公司完成阶段性工作所需要的最短时间。
样例输入 Sample Input
6 3
1 2 3
1 6 4
3 1 7
4 3 6
3 5 5
3 6
2 5
4 5样例输出 Sample Output
11数据范围及提示 Data Size & Hint
样例解释:
将第 1 条航道改造成虫洞: 则三个计划耗时分别为:11,12,11,故需要花费的时间为 12。
将第 2 条航道改造成虫洞: 则三个计划耗时分别为:7,15,11,故需要花费的时间为 15。
将第 3 条航道改造成虫洞: 则三个计划耗时分别为:4,8,11,故需要花费的时间为 11。
将第 4 条航道改造成虫洞: 则三个计划耗时分别为:11,15,5,故需要花费的时间为 15。
将第 5 条航道改造成虫洞: 则三个计划耗时分别为:11,10,6,故需要花费的时间为 11。
故将第 3 条或第 5 条航道改造成虫洞均可使得完成阶段性工作的耗时最短,需要花费的时间为 11。
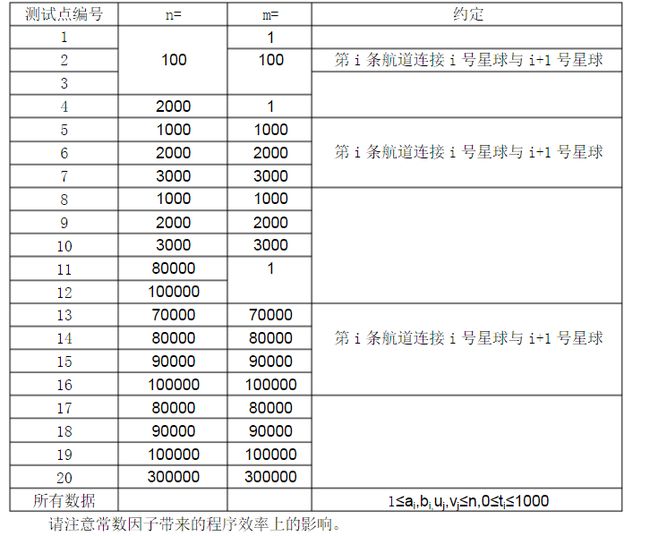
测试数据及约定:
题解:
最开始参考的wkingG的题解:http://www.cnblogs.com/wkingG/p/5021197.html
我们首先需要计算出每一条路径的长度,计算长度这儿可以直接用差分数组优化,这样就不用再用树链剖分然后线段树计算长度,可以把代码优化不少。
计算完长度之后就对长度进行排序。
这个题目就是最大值最小于是自然想到二分【这儿也有优化因为我们只能建一个黑洞,所以二分的左端点是最长的距离-1000或者是0中间较大的值因为这个0我被卡了半天![]() 】
】
我们二分了之后就对路径长度大于MID的路径全部打上标记并计算大于MID的边的条数S,然后就在最后处理完以后一次性把标记全部压到叶子节点【也就是每一条边】,比较得出被标记S次且最大的那条边,之后看我最大的那条边减去这权值是否小于MID如果是的,就成功了可以调整边界。这里有点优化,因为我需要建黑洞的边没有修改操作,所以是具有不变的单调性的,于是我们可以直接开一个数组来记忆化,当我有S条边需要建黑洞的时候,我应该建黑洞的那条边的权值。
上面贪心证明如下:我们一共有s条边大于MID所以我们需要把这S条边全部调整至MID以下,那么如果没有任何一条边被标记S次着代表我这次无论修改那条边总有边没有被修改到,所以说我这次调整也就不成功,我修改最大的就代表如果最长的路径减去最长的边之后小于MID,那么我后面的边减去最长的边之后必定小于MID,反之如果最大的减去最长的边之后大于MID那么我的时间就大于MID了。
下面贴代码
【差分数组版本】
这个版本跑得挺快的在BZOJ排名14
![]()
/* 作者:WZH 题目:p4632 NOIP[2015] 运输计划 */
#include <algorithm>
#include <iostream>
#include <cstring>
#include <string>
#include <queue>
#include <cstdio>
using namespace std;
const int MAXN = 1600000;
inline int max(int a,int b){ return a > b ? a : b;}
inline int min(int a,int b){ return a < b ? a : b;}
int head[MAXN],V[MAXN],SUM[MAXN],MARK[MAXN],N,M,e = 1,dfn,ql,qr,ans,s,C[MAXN],Data[MAXN];
int MAX;
//V 当修改条数为s 需要修改的黑洞权值
inline int read(){
int x = 0,f = 1;char ch = getchar();
while(ch < '0' || '9' < ch) {if(ch == '-') f = -1;ch = getchar();}
while('0'<= ch && ch <='9') {x = x * 10 + ch - '0';ch = getchar();}
return x * f;
}
struct node{
int v,c,next;
}edge[MAXN];
struct SLPF{
int Fa,Son,Num,Top,Size,Deep,C;
}P[MAXN];
struct problem{
friend bool operator < (const problem &a,const problem &b){
return a.dist > b.dist;
}
int u,v,dist;
}PRO[MAXN];
inline void addedge(int u,int v,int c){
edge[e].next = head[u];edge[e].v = v;edge[e].c = c;head[u] = e++;
edge[e].next = head[v];edge[e].v = u;edge[e].c = c;head[v] = e++;
}
inline void init(){
N = read();M = read();
int u,v,c;
for(int i = 1;i < N;i++){
u = read();v = read();c = read();
addedge(u,v,c);
}
for(int i = 1;i <= M;i++){
PRO[i].u = read();PRO[i].v = read();
}
}
inline void dfs_1(int u,int h){
P[u].Size = 1;P[u].Deep = h;P[u].Son = -1;
for(int i = head[u];i;i = edge[i].next){
int v = edge[i].v;
if(!P[v].Deep){
P[v].Fa = u;
dfs_1(v,h+1);
P[u].Size += P[v].Size;
if(P[v].Size > P[P[u].Son].Size) P[u].Son = v,P[u].C = edge[i].c;
}
}
}
inline void dfs_2(int u,int top,int c){
P[u].Top = top;P[u].Num = ++dfn;Data[dfn] = c;
if(P[u].Son > 0) dfs_2(P[u].Son,top,P[u].C);
for(int i = head[u];i;i = edge[i].next)
if(!P[edge[i].v].Num) dfs_2(edge[i].v,edge[i].v,edge[i].c);
}
inline void query_dist(int x,int y,int &v)
{
while(P[x].Top != P[y].Top){
int tx = P[x].Top,ty = P[y].Top;
if(P[tx].Deep >= P[ty].Deep){
ql = P[tx].Num;qr = P[x].Num;
v += SUM[qr] - SUM[ql] + Data[ql];x = P[tx].Fa;
}
else {
ql = P[ty].Num;qr = P[y].Num;
v += SUM[qr] - SUM[ql] + Data[ql];y = P[ty].Fa;
}
}
if(x == y) return;
else if(P[x].Deep < P[y].Deep){
ql = P[x].Num;qr = P[y].Num;
v += SUM[qr] - SUM[ql];
}
else {
ql = P[y].Num;qr = P[x].Num;
v += SUM[qr] - SUM[ql];
}
}
inline void query_push(int o,int L,int R){
if(L == R){if(MARK[o] == s) MAX = max(MAX,Data[L]);;MARK[o] = 0;return;}
int MID = (L + R) >> 1;
MARK[o<<1] += MARK[o];MARK[o<<1|1] += MARK[o];MARK[o] = 0;
query_push(o<<1,L,MID);
query_push(o<<1|1,MID+1,R);
}
inline void MARKING(int o,int L,int R){
if(ql <= L && R <= qr){++MARK[o];return;}
int MID = (L + R) >> 1;
if(ql <= MID) MARKING(o<<1,L,MID);
if(MID < qr) MARKING(o<<1|1,MID+1,R);
}
inline void query_mark(int x,int y){
while(P[x].Top != P[y].Top){
int tx = P[x].Top,ty = P[y].Top;
if(P[tx].Deep >= P[ty].Deep){
ql = P[tx].Num;qr = P[x].Num;
MARKING(1,1,N);
x = P[tx].Fa;
}
else {
ql = P[ty].Num;qr = P[y].Num;
MARKING(1,1,N);
y = P[ty].Fa;
}
}
if(x == y) return;
else if(P[x].Deep < P[y].Deep){
ql = P[P[x].Son].Num;qr = P[y].Num;
MARKING(1,1,N);
}
else {
ql = P[P[y].Son].Num;qr = P[x].Num;
MARKING(1,1,N);
}
}
inline int Binary_s(int x){
int L = 1,R = M + 1,MID;
while(L != R)
{
MID = (L + R) >> 1;
if(PRO[MID].dist > x) L = MID + 1;
else R = MID;
}
return L - 1;
}
inline bool check(int MID)
{
if(V[s] && PRO[1].dist - V[s] <= MID ) return true;
if(V[s]) return false;
for(int i = 1;i <= s;i++){
ql = PRO[i].u;qr = PRO[i].v;
query_mark(ql,qr);
}
MAX = 0;query_push(1,1,N);
if(MAX == 0) return false;
if(PRO[1].dist - MAX <= MID) {V[s] = MAX;return true;}
else {V[s] = MAX;return false;}
}
inline int Binary()
{
for(int i = 1;i <= M;i++)
query_dist(PRO[i].u,PRO[i].v,PRO[i].dist);
sort(PRO+1,PRO+1+M);
int L = max(PRO[1].dist - 1005,0),R = PRO[1].dist;
while(L!=R)
{
int MID = (L + R) >> 1;
s = Binary_s(MID);
if(check(MID)) R = MID;
else L = MID + 1;
}
printf("%d",L);
}
int main()
{
init();
dfs_1(1,1);
dfs_2(1,1,0);
for(int i = 1;i <= N;i++) SUM[i] = SUM[i-1] + Data[i];
Binary();
return 0;
}【用线段数计算路径】
#include <algorithm>
#include <iostream>
#include <cstring>
#include <string>
#include <queue>
#include <cstdio>
using namespace std;
const int MAXN = 2000000;
int head[MAXN],V[MAXN],SUM[MAXN],MARK[MAXN],N,M,e = 1,dfn,ql,qr,ans,s,C[MAXN],Data[MAXN];
int MAX;
//V 当修改条数为s 需要修改的黑洞权值
inline int read(){
int x = 0,f = 1;char ch = getchar();
while(ch < '0' || '9' < ch) {if(ch == '-') f = -1;ch = getchar();}
while('0'<= ch && ch <='9') {x = x * 10 + ch - '0';ch = getchar();}
return x * f;
}
struct node{
int v,c,next;
}edge[MAXN];
struct SLPF{
int Fa,Son,Num,Top,Size,Deep,C;
}P[MAXN];
struct problem{
friend bool operator < (const problem &a,const problem &b){
return a.dist > b.dist;
}
int u,v,dist;
}PRO[MAXN];
inline void addedge(int u,int v,int c){
edge[e].next = head[u];edge[e].v = v;edge[e].c = c;head[u] = e++;
edge[e].next = head[v];edge[e].v = u;edge[e].c = c;head[v] = e++;
}
inline void init(){
N = read();M = read();
int u,v,c;
for(int i = 1;i < N;i++){
u = read();v = read();c = read();
addedge(u,v,c);
}
for(int i = 1;i <= M;i++){
PRO[i].u = read();PRO[i].v = read();
}
}
void dfs_1(int u,int h){
P[u].Size = 1;P[u].Deep = h;P[u].Son = -1;
for(int i = head[u];i;i = edge[i].next){
int v = edge[i].v;
if(!P[v].Deep){
P[v].Fa = u;
dfs_1(v,h+1);
P[u].Size += P[v].Size;
if(P[v].Size > P[P[u].Son].Size) P[u].Son = v,P[u].C = edge[i].c;
}
}
}
void dfs_2(int u,int top,int c){
P[u].Top = top;P[u].Num = ++dfn;Data[dfn] = c;
if(P[u].Son > 0) dfs_2(P[u].Son,top,P[u].C);
for(int i = head[u];i;i = edge[i].next)
if(!P[edge[i].v].Num) dfs_2(edge[i].v,edge[i].v,edge[i].c);
}
void update(int o,int L,int R)
{
if(L == R) {SUM[o] = Data[L];return;}
int MID = (L + R) >> 1;
update(o << 1,L,MID);
update(o << 1|1,MID + 1,R);
SUM[o] = SUM[o<<1] + SUM[o<<1|1];
}
void query(int o,int L,int R){
if(ql <= L && R <= qr){ans += SUM[o];return;}
int MID = (L + R) >> 1;
if(ql <= MID) query(o<<1,L,MID);
if(MID < qr) query(o<<1|1,MID+1,R);
}
void query_dist(int x,int y,int &v)
{
while(P[x].Top != P[y].Top){
int tx = P[x].Top,ty = P[y].Top;
if(P[tx].Deep >= P[ty].Deep){
ql = P[tx].Num;qr = P[x].Num;
ans = 0;query(1,1,N);
v += ans;x = P[tx].Fa;
}
else {
ql = P[ty].Num;qr = P[y].Num;
ans = 0;query(1,1,N);
v += ans;y = P[ty].Fa;
}
}
if(x == y) return;
else if(P[x].Deep < P[y].Deep){
ql = P[x].Num;qr = P[y].Num;
ans = 0;query(1,1,N);
v += ans - Data[ql];
}
else {
ql = P[y].Num;qr = P[x].Num;
ans = 0;query(1,1,N);
v += ans - Data[ql];
}
}
void query_push(int o,int L,int R){
if(L == R){if(MARK[o] == s) MAX = max(MAX,Data[L]);return;}
int MID = (L + R) >> 1;
MARK[o<<1] += MARK[o];MARK[o<<1|1] += MARK[o];MARK[o] = 0;
query_push(o<<1,L,MID);
query_push(o<<1|1,MID+1,R);
}
void MARKING(int o,int L,int R){
if(ql <= L && R <= qr){++MARK[o];return;}
int MID = (L + R) >> 1;
if(ql <= MID) MARKING(o<<1,L,MID);
if(MID < qr) MARKING(o<<1|1,MID+1,R);
}
void query_mark(int x,int y){
while(P[x].Top != P[y].Top){
int tx = P[x].Top,ty = P[y].Top;
if(P[tx].Deep >= P[ty].Deep){
ql = P[tx].Num;qr = P[x].Num;
MARKING(1,1,N);
x = P[tx].Fa;
}
else {
ql = P[ty].Num;qr = P[y].Num;
MARKING(1,1,N);
y = P[ty].Fa;
}
}
if(x == y) return;
else if(P[x].Deep < P[y].Deep){
ql = P[P[x].Son].Num;qr = P[y].Num;
MARKING(1,1,N);
}
else {
ql = P[P[y].Son].Num;qr = P[x].Num;
MARKING(1,1,N);
}
}
inline int Binary_s(int x){
int L = 1,R = M + 1,MID;
while(L != R)
{
MID = (L + R) >> 1;
if(PRO[MID].dist > x) L = MID + 1;
else R = MID;
}
return L - 1;
}
inline bool check(int MID)
{
if(V[s] && PRO[1].dist - V[s] <= MID ) return true;
if(V[s]) return false;
memset(MARK,0,sizeof(MARK));
for(int i = 1;i <= s;i++){
ql = PRO[i].u;qr = PRO[i].v;
query_mark(ql,qr);
}
MAX = 0;query_push(1,1,N);
if(MAX == 0) return false;
if(PRO[1].dist - MAX <= MID) return true;
else return false;
}
inline int Binary(){
for(int i = 1;i <= M;i++)
query_dist(PRO[i].u,PRO[i].v,PRO[i].dist);
sort(PRO+1,PRO+1+M);
int L = max(PRO[1].dist - 1000,0),R = PRO[1].dist;
while(L!=R)
{
int MID = (L + R) >> 1;
s = Binary_s(MID);
if(check(MID)) R = MID;
else L = MID + 1;
}
printf("%d",L);
}
int main()
{
init();
dfs_1(1,1);
dfs_2(1,1,0);
update(1,1,N);
Binary();
return 0;
}时间比较放在这儿大家参考一下:
![]()