编译原理 NFA_DFA代码实现 bfs+dfs+状态压缩 伪代码
这是上个月的作业了,由于当初发怕被抄袭,这个blog现在补上。
编译原理老师给我们布置了一个作业,要求用程序实现NFA_DFA的转化,并且要画图!画图!画图!日狗的事情说三遍!
对于我这个ACMer,输出表格的部分分分钟就编好了,bfs、dfs、状态压缩,程序高效无比,bug基本都清了。看看其他人还字符串比较爆搜的。。。这要是在比赛里不超时才怪!!!然后我们用了10%的时间和精力编了前半部分,用了90%的精力编写图像输出程序。。。
先给大家看看我们的前半部分是咋弄的,我用c++写的。想看代码?大哥打赏打赏use俩积分下载我上传的资源去>_<
http://download.csdn.net/detail/qdbszsj/9307911
这是伪代码,nb的人有伪代码基本就能敲出来了
1.初始化(init):
声明各种变量,开数组,并清空。
2.输入(input):
按照交互界面提示的格式,将nfa图输入。
3.运行核心算法程序(bfs宽度优先搜索):
声明一个队列q,q内存储int型数据,代表状态压缩后的一个集合;
放入起点0 通过dfs算法(深度优先搜索,具体实现见下文附录)得出的集合a;
在映射s中存入a,key值为a,权值为n++(n起始为1);
While(队列不为空){
令f=队列的第一个元素;
队列q.pop掉一个元素;
统计的集合个数num_of_jihe++;
for(i从0~图中权值的种类数){
对f进行dfs操作,得出中间结果;
对中间结果再dfs一遍得出最终集合;
If(结果不为空并且结果在映射中不存在){
映射中放入结果;
队列q.push进去结果;
}
}
}
然后说说我们的画图算法。。。那是一个及其日狗的算法。首先我们是用c++做表格,导出到txt里,然后用c#读取数据,画的表格,我搞ACM有些依赖c++的STL了,懒得直接用c#写程序。然而c++又没法输出质量比较高的图形,于是乎……
实际上,要想这个图画的没bug,费事的很,因为闹不好就会有俩什么玩意重合在一起了
首先:
弄个大圆,然后有几个结点,就平均分配给他们坐标,让他们在大圆上。
然后:
需要连线的连线
then:
在线上写abcd啥的,再标注上箭头
finish。。。是不是看起来十分轻松哇,然而弄这玩意弄的比前面要难好多。
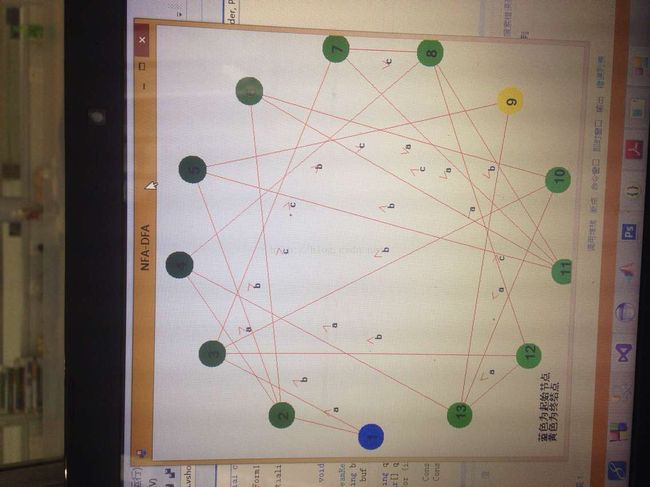
这个图画的,个人认为比较有创造力的一点是我们用了向量法,就给大家提示到这了,用向量!单位向量and法向量,没有向量,咋画箭头啊,最后我们各种加x*单位向量和法向量,乱搞搞也搞出来了。这是个效果图。。。。代码,还是要下载滴:http://download.csdn.net/detail/qdbszsj/9308021
附言:
状态压缩的基本思想:
因为计算机中的数据用二进制存储,所以我们可以用一个int型的数表示一个集合,第i位为1就代表集合中存在i,为0反之。
例如:
00001101就可以代表一个集合(0,2,3)
10010010001可以代表(0,4,7,10)
Dfs函数的实现:
int dfs(int from,char key){//from代表从编号为from的点开始dfs,key代表要经过的权值
int ans=0;//初始化集合为空
if(key=='0'){//如果要dfs空
for(int i=0;i<G[from].size();i++){
if(G[from][i].v==key&&vis[G[from][i].to]==0){
ans|=(1<<G[from][i].to);//把要去的点并进集合
vis[G[from][i].to]=1;//为了避免重复将走过的点标记为1,没走过的再走
ans|=dfs(G[from][i].to,key);//递归地调用dfs
}
}
ans|=(1<<from);//不能落下起点啊
}
else{//这是dfs权值不为0的路径,因为只走一步,并且自己不算集合里,所以不用递归,最后也不用并起点
for(int i=0;i<G[from].size();i++){
if(G[from][i].v==key){
ans|=(1<<G[from][i].to);
}
}
}
// cout<<"dfs";change(ans);
return ans;
}