BZOJ 1031

BZOJ 1031

Problem

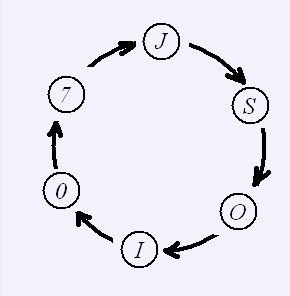
  喜欢钻研问题的JS 同学，最近又迷上了对加密方法的思考。一天，他突然想出了一种他认为是终极的加密办法：把需要加密的信息排成一圈，显然，它们有很多种不同的读法。例如下图，可以读作：

JSOI07 SOI07J OI07JS I07JSO 07JSOI 7JSOI0 把它们按照字符串的大小排序： 07JSOI 7JSOI0 I07JSO JSOI07 OI07JS SOI07J 读出最后一列字符：I0O7SJ，就是加密后的字符串（其实这个加密手段实在很容易破解，鉴于这是突然想出来的，那就^^）。但是，如果想加密的字符串实在太长，你能写一个程序完成这个任务吗？

Limits

Time Limit(s): 10（1s足以）

Memory Limit(MB): 162

字符串长度N: [1, 10^5]

字符集: 字母，数字，符号

Solution

  设输入的字符串为S1，将S1延长一倍，得到S=S1+S1，S长度为2N；对S构造后缀数组、height数组，在2N个后缀中，把所有起始位置（sa[i]）大于等于N的后缀排除。按后缀数组的顺序，将剩余的N个后缀的每第N个字符拼接起来，即为加密字符串。

More

先配图解释样例。

样例字符串S1="JSOI07"，S=S1+S1="JSOI07JSOI07"，N=6，则S长度为2N=12；S有12个后缀，从短到长分别是：“7”，“07”，“I07”，“OI07”，"SOI07"，“JSOI07”，"7JS0I07"，“07JSOI07”，"I07JSOI07"，“OI07JSOI07”，"SOI07JSOI07"，“JSOI07JSOI07”；把12个后缀按照字典序排序，得到如下图。

（图中记录12个后缀的字典序 以及 在原串“JSOI07JSOI07”中的起始位置，0开始）

根据题目要求，只关心起始位置在[0，6)区间内的6个后缀，按照后缀数组的顺序（图中字符串字典序）找出。得到：“07JSOI07”，“7JS0I07”，“I07JSOI07”，“JSOI07JSOI07”，“OI07JSOI07”，“SOI07JSOI07”。将6个后缀的每第6个字符拼接起来，得到“I0O7SJ”，即为加密字符串。

再证明上述做法的正确性。

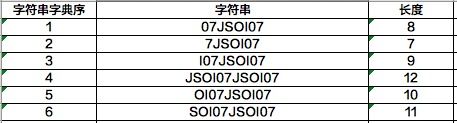
上述做法中，理解按照字典序排序所有后缀来构造后缀数组的方法由为关键。可以发现多个字符串按照字典序排序后，有那么一些微妙的性质。下图为剩余的6个后缀，且已按照字典序排好序。

上图6个字符串长度均不一样，但若每个字符串都取相等长度的前缀后，可以发现6个前缀的字典序可以与母字符串的字典序保持一致。换句话说，任取图中两个字符串Si、Sj，不失一般性，保证Si<Sj，再令Sn=Si[0]Si[1]......Si[L-1]，Sm=Sj[0]Sj[1]......Sj[L-1]（L>=0）；Sn，Sm分别是Si 与Sj 取长度为L的前缀；可以证明Sn<=Sm一定成立。

下面给出证明。考虑导致Si<Sj 的位置p，若p<L，那么Sn<Sm必然成立；若p>=L，说明Sn=Sm，但存在一个位置大于等于L的字符使得Si<Sj。由此可知Sn<=Sm成立。

这样就说明了Solution中“按后缀数组的顺序，将剩余的N个后缀的每第N个字符拼接起来，即为加密字符串”做法的正确性。

Complexity

Time Complexity: O(N*logN)

Memory Complexity: O(8*N)

Source

BZOJ 1031

Code

BZOJ 1031 From My Github