路径动画

    上周末上司找到我提出要实现几个常见的路径动画算法，人家soya动画引擎已经有了类似的功能，而我们的cantk暂时还没有对应的功能。加入路径动画的最终效果要达到物体能够沿着一定的轨迹运动，配合各种差值算法，使得物体更加生动。原理说起来很简单，就是要去实现canvas内置的几个API，如lineTo. arcTo. bezierCurveTo. quadraticCurveTo等, 物体运动除了要给出某一时间点的坐标还得给出相应的角度信息。当时给的时间是两天，可是我足足花了一个星期的时间才把它搞定，深深的罪恶感～

先从简单的说起

lineTo(直线)

PathAnimation.prototype.lineTo = function(x, y, duration, interpolator) {
    var path = {
        ex: x,
        ey: y,
        duration: duration,
        interpolator: interpolator,
        type: PathAnimation.TYPE_LINE
    };

    this.__paths.push(path);

    return this;
}

    因为要现实链式调用, 所以调用函数的时候要先记录一些路径信息。lineTo函数只需要传入线段终点坐标即可，起点坐标由前一次绘制的终点坐标决定，或者为传入的初始坐标。

//获取方向
 PathAnimation.prototype.__lineDirection = function(path, prevPos, easePercent) {
    return PathAnimation.Math.calcPointsAngle(prevPos.x, prevPos.y, path.ex, path.ey); 
}

//获取坐标
PathAnimation.prototype.__linePosition = function(path, prevPos, percent) {
    return {
        x: prevPos.x + (path.ex - prevPos.x) * percent,
        y: prevPos.y + (path.ey - prevPos.y) * percent
    };
}

`lineTo的实现还是比较简单，稍微回忆下学过的数学知识就能写出来。

quadraticCurveTo(抛物线)

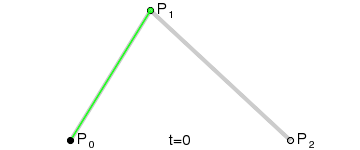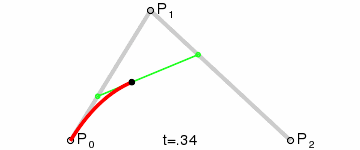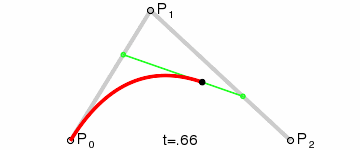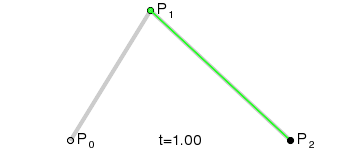
quadraticCurveTo是二次贝塞尔曲线的图像表现。只有一个控制点，用来控制抛物线的曲率。抛物线为：以起点-控制点 和控制点-终点两条直线为切线，从起点到终点构成的抛物线。

PathAnimation.prototype.quadraticCurveTo = function(cx, cy, ex, ey, duration, interpolator) {
    var path = {
        cx: cx,
        cy: cy,
        ex: ex,
        ey: ey,
        duration: duration,
        interpolator: interpolator,
        type: PathAnimation.TYPE_QUAD
    };

    this.__paths.push(path);

    return this;
}

曲线方程:
这样我们就能轻易的求出某个时间点的坐标。

PathAnimation.prototype.__quadraticPosition = function(path, prevPos, percent) {
    var arrX = [];
    arrX.push(prevPos.x);
    arrX.push(path.cx);
    arrX.push(path.ex);

    var arrY = [];
    arrY.push(prevPos.y);
    arrY.push(path.cy);
    arrY.push(path.ey);

    var x = Math.pow(percent, 2)*(arrX[0] - 2*arrX[1] + arrX[2]) + percent*(2*arrX[1] - 2*arrX[0]) + arrX[0];
    var y = Math.pow(percent, 2)*(arrY[0] - 2*arrY[1] + arrY[2]) + percent*(2*arrY[1] - 2*arrY[0]) + arrY[0];

    return {x: x, y: y};
}

求方向得先知道某个时间点的切线斜率，而求斜率就得先求出函数的倒数,直接对曲线方程求倒即可。

PathAnimation.prototype.__quadraticDirection = function(path, prevPos, easePercent) {
    var arrX = [];
    arrX.push(prevPos.x);
    arrX.push(path.cx);
    arrX.push(path.ex);

    var arrY = [];
    arrY.push(prevPos.y);
    arrY.push(path.cy);
    arrY.push(path.ey);

    var disx = 2*(arrX[0] - 2*arrX[1] + arrX[2])*easePercent + (-2*arrX[0] + 2*arrX[1]);
    var disy = 2*(arrY[0] - 2*arrY[1] + arrY[2])*easePercent + (-2*arrY[0] + 2*arrY[1]);

    if(disx == 0) {
        return 90;
    }
    else {
        return PathAnimation.Math.toAngle(Math.atan(disy/disx));  
    }
}

bezierCurveTo(贝塞尔曲线)

bezierCurveTo的实现比抛物线多了一个控制点。大致的实现 思路都是类似，这里就不放代码了。
曲线方程：

sinTo(正弦曲线)

PathAnimation.prototype.sinTo = function(amplitude, cycle, waveLength, duration, interpolator) {
    var path = {
        cycle: cycle,
        duration: duration,
        amplitude: amplitude,
        waveLength: waveLength,
        interpolator: interpolator,
        type: PathAnimation.TYPE_SIN
    };

    this.__paths.push(path);

    return this;
}

实现正弦曲线的时候考虑用户在使用上的便利。决定以前一个路径的终点作为标准正弦曲线的原点(0, 0)点，计算坐标的时候需要转换坐标。在调用接口的时候只需要传入振幅，周期以及波长(以周期为单位)即可。这样就不用考虑初相位以及在y轴的偏移了。

//计算角速度以及曲线结束坐标
PathAnimation.prototype.__initSin = function(path, prevPos) {
    if(path.ex) return path;

    path.omg = 2*Math.PI/path.cycle;
    path.sx = prevPos.x;
    path.sy = prevPos.y;

    path.ex = path.waveLength + prevPos.x;
    path.ey = path.amplitude * Math.sin(path.omg*path.waveLength) + prevPos.y;

    return path;
}

//获取某个时间点的坐标
PathAnimation.prototype.__sinPosition = function(path, prevPos, percent) {
    var x = path.waveLength*percent;
    var y = path.amplitude * Math.sin(path.omg*x);

    return {
        x: x + path.sx,
        y: y + path.sy
    };
}
//获取方向
PathAnimation.prototype.__sinDirection = function(path, prevPos, percent) {
    path = this.__initSin(path, prevPos);

    var x = percent * path.waveLength;
    var slope = path.amplitude * path.omg * Math.cos(path.omg*x);

    return PathAnimation.Math.toAngle(Math.atan(slope)); 
}

arcTo(圆弧+直线)

实现这个功能花了不少时间，对canvas内置对应函数实现的不够理解，数学知识也差不多忘光了。先上个图：

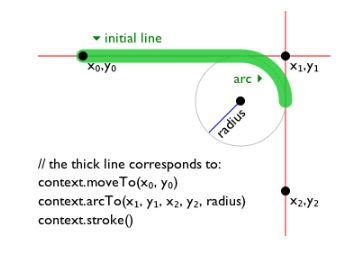
需要注意的是arcTo的路径受到前一个坐标点的影响，而不仅仅包含圆弧。
两个要点：

1. 计算圆心坐标
2. 计算两个切点坐标

arcTo的长度等于起点到第一个切点的长度加上两个切点构成的圆弧的长度。

PathAnimation.prototype.arcTo = function(x1, y1, x2, y2, radius, duration, interpolator) {
    var path = {
        sx: x1,
        sy: y1,
        dx: x2,
        dy: y2,
        r: radius,
        duration: duration,
        interpolator: interpolator,
        type: PathAnimation.TYPE_ARCTO
    };

    this.__paths.push(path);

    return this;
}

代码略长，具体实现在这里：path-animation