山东省第五届ACM大学生程序设计竞赛-angry_birds_again_and_again(积分)
angry_birds_again_and_again
Time Limit: 2000ms Memory limit: 65536K 有疑问?点这里^_^
题目描述
The problems called "Angry Birds" and "Angry Birds Again and Again" has been solved by many teams in the series of contest in 2011 Multi-University Training Contest.
This time we focus on the yellow bird called Chuck. Chuck can pick up speed and distance when tapped.
You can assume that before tapped, Chuck flies along the parabola. When tapped, it changes to fly along the tangent line. The Chuck starts at the coordinates (0, 0). Now you are given the coordinates of the pig (Px, 0), the x-coordinate of the tapping position (Tx) and the initial flying angle of Chuck (α).
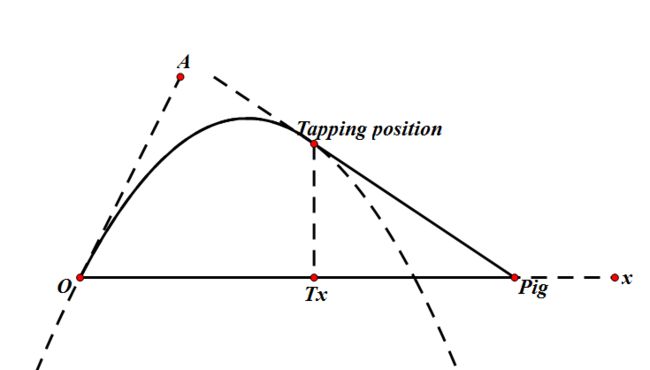

∠AOx = α
Please calculate the area surrounded by Chuck’s path and the ground.(The area surrounded by the solid line O-Tapping position-Pig-O)
输入
The first line contains only one integer T (T is about 1000) indicates the number of test cases. For each case there are two integers, px tx, and a float number α.(0 < Tx ≤ Px ≤ 1000, 0 < α <
 ) .
) .
输出
One line for each case specifying the distance rounded to three digits.
示例输入
1 2 1 1.0
示例输出
0.692
提示
来源
2014年山东省第五届ACM大学生程序设计竞赛
示例程序
题目意思:
给出图中点TX的横坐标tx,点Pig的横坐标px,角AOT,求图中实线部分的面积。
解题思路:
先用积分求出O点到TX点抛物线与x轴所成部分的面积,再求TX点到Pig点所成的直角三角形面积,两部分相加即为题目所求答案。
设抛物线y=ax^2+bx+c,由于y过原点,则c=0;
对y求导:y‘=2ax+b;
代入O点(0,0),则y’=b为抛物线在O点(0,0)处的斜率,即 tan(角AOT)=斜率y‘=b;
代入点Tap(tx,y(tx)),则y’=2a*tx+b为抛物线在点Tap(tx,y(tx))处的斜率,即:
由TX点到Pig点所成的直角三角形两直角边的正切值y(tx)/(px-tx),
得抛物线在点Tap(tx,y(tx))处的斜率:(注意有负号!因为)-y(tx)/(px-tx)=y’=2a*tx+b
得2a*tx+b= - ( a*tx^2+b*tx)/(px-tx) ,化简得:a=(-b*px)/(2.0*tx*(px-tx)+tx*tx);
至此,抛物线y中abc都求了出来,下面进行积分;
y=ax^2+bx 在[0,tx]范围内积分,则 [(a/3)*x^3+(b/2)*x^2](上tx下0);
直角三角形面积:0.5*(px-tx)*(a*tx*tx+b*tx);
相加。
The End。
下面上代码:
/*
*Copyright (c)2016,烟台大学计算机与控制工程学院
*All rights reserved.
*文件名称:area.cpp
*作 者:单昕昕
*完成日期:2016年4月19日
*版 本 号:v1.0
*/
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include <iomanip>
#include<algorithm>
using namespace std;
int main()
{
int t;
cin>>t;
while(t--)
{
double a,b,o,ans,px,tx;//用float会WA!!
cin>>px>>tx>>o;
b=tan(o);//斜率
//cout<<b<<endl;
a=(-b*px)/(2.0*tx*(px-tx)+tx*tx);//x^2的系数
//cout<<a<<endl;
ans=tx*tx*tx*a/3.0+tx*tx*b/2.0;//积分
ans+=(0.5*(px-tx)*(a*tx*tx+b*tx));//加上三角形面积
cout<<setiosflags(ios::fixed)<<setprecision(3)<<ans<<endl;
}
return 0;
}