跳跃表

如何在大量元素中去查找某个元素。例如在下面的“大量元素”的数组中

对于上面的情况无论是查找3还是查找8，只有一种办法，那就是遍历。时间复杂度是O(N)

但是举一个生活中的例子，我们在查新华字典的时候，没有人会一页一页的翻吧，肯定是翻到中间看看，然后再决定往左边查，还是往右边查。

显然，可以把元素排序放在一个数组中，这样就可以利用二分查找了。查字典也算是二分查找的一个实际例子。二分查找的时间复杂度是O(logN)

利用二分查找是有前提限制的：

1：元素已排序

2：元素可以随机访问

二分查找要求元素可以随机访问，所以决定了需要把元素存储在连续内存。这样查找确实很快，但是插入和删除元素的时候，为了保证元素的有序性，就需要大量的移动元素了。（当然如果删除操作较少的话，也可以用懒惰删除，被删除的元素做个标记，但并不实际从内存中清楚，所以也不用移动元素。但是对于插入还是没有办法）

所以，现在我们需要的是一个能够进行二分查找，又能快速添加和删除元素的数据结构。这就非(平衡)二叉查找树莫属了。

此时，我们可以利用树这个模型，对1,2,3,4,5,6这6个元素够造成一个二叉树，如下：

显然，上面这棵树太坑爹了。把自己的头右转45°或者把显示器左转45°，我们会发现，这TM就是一个链表。这棵树不符合快速查找元素的要求，原因就是，每个节点的左右子树之差>1，也就是不平衡。不平衡就导致了树的高度过高，所以没有办法根据一个节点筛选掉一半的子结点(左右子结点个数不相等)

然后，带有高度平衡条件的AVL树，是下面这样的。

对于这样一棵树，查找元素就是变相的二分查找。（插入，删除也有了保证，直觉上只需修改几个指针）

但是，由于AVL树要求高度平衡，不论是插入还是查找，被操作节点到根节点的整条路径上的所有节点都要判断，是否打破了平衡条件，从而LL, LR, RR, RL旋转。(当然了，实现一颗AVL树也不困难，但是相对于skiplist还是复杂些)

RB树是一种对平衡要求相对略低的AVL树。(类似于2-3树)

但是，无论是高度平衡的AVL还是RB树，自己编写起来难度都比较大。虽然说已经有了现成的set/map(基于红黑树实现)。

通过上面的几个图，我们可以发现，二分查找和AVL树为什么那么高效，原因就是：每比较一次，就能筛掉一半元素。

就像我们查字典一样，没有人会傻傻的从第一页开始一页一页的查，肯定是先翻到字典中间看看，然后决定继续查字典的前半部分还是后半部分。

接下来，我们就来看看跳跃表。

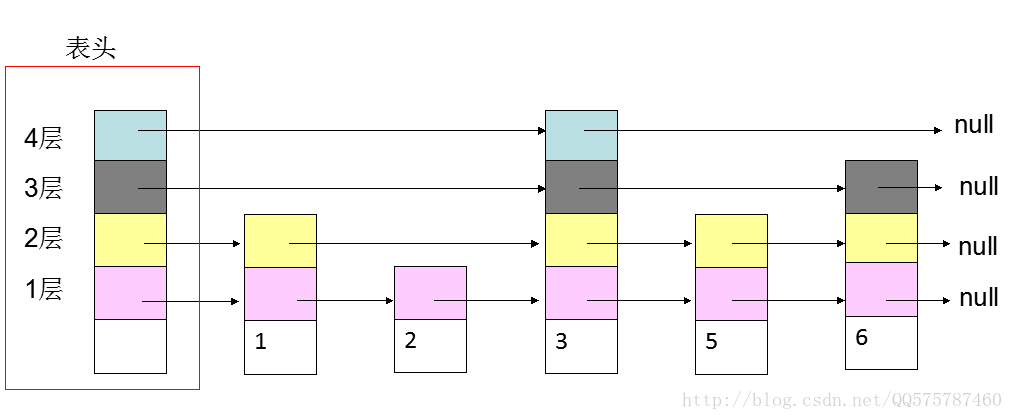
之所以成为跳跃表，就是因为每个节点会额外保存几个指针，间隔的指向后继的节点。

具体的查找，删除，插入原理。这里已经讲了。点击打开链接

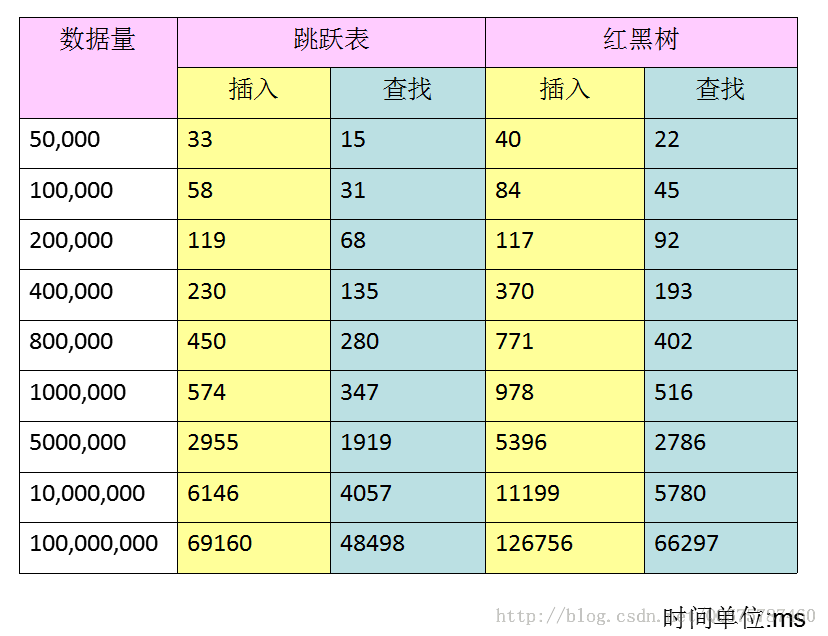
我自己实现一个最高为12层的跳跃表，并与红黑树的效率做了对比。

可以看到，数据量很大时，跳跃表的优势显著(当然skiplist很浪费内存这个劣势也很明显)。