算法之大整数乘法

  大数的表示方法有很多种，最易懂的而且最跟手工计算方式最接近的方式是通过字符数组来保存大数，数组的每个元素保存大数的一个十进制数字，这种方式操作比较简单，但是这种方式需要较多的额外运算，所以效率低下。另一种方式是采用链表作为存储结构，这种方式可以适应不同长度的大数，但是这种方式的存储效率很低，对本身就需要不少内存空间的大数运算来说负担很重，而且频繁的堆操作和解引用操作会大量增加开销，此外链表存储的不连续性也大降低了CPU的高速缓存cache的命中率，不利于编译器优化速度。被广泛采用的效率较高的方式是用B进制数组存储大数，即把大数转化成B进制表示，数组的每个元素存储这个B进制数的一个B进制位，减少了循环的次数，有利于提高效率。

  下面首先用模拟手工计算的方法来进行计算，程序接收两个以字符串形式输入的数字，然后把这两数字字符串分别存入两个整型数组中，数组的每一元素存储相应数字的一个十进制位。然后通过两重 for 循环来模拟手工计算的过程。程序化如下：

#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#define NUM_LEN   50//数字的最大长度

void main()
{
	int i, n, temp = 0, p, k;

	char num1[NUM_LEN], num2[NUM_LEN];
	puts("Please input the first number:");
	gets(num1);
	puts("\nPlease input the second number:");
	gets(num2);
	int len1 = strlen(num1);
	int len2 = strlen(num2);
	int *arr1 = (int *)malloc(sizeof(int) * len1);
	int *arr2 = (int *)malloc(sizeof(int) * len2);

	for(i = 0; i < len1; i++)
	{
		arr1[i] = (int)num1[i] - 48;   //把字符转换成对应的整数
	}
	for(i = 0; i < len2; i++)
	{
		arr2[i] = (int)num2[i] - 48;
	}

	int *result = (int *)malloc(sizeof(int) * (len1 + len2));
	n = len1 + len2 - 1;
	for(i = 0; i <= n; i++)
	{
		result[i] = 0;   //初始化结果数组
	}

	for(i = len1 - 1; i >= 0; i--)
	{
		p = arr1[i];
		for(k = len2 - 1; k >= 0; k--)
		{
			temp = result[n] + p * arr2[k];
			if(temp >= 10)   //如果temp>=10，则应该进位
			{
				result[n] = temp%10;   //取个位
				result[n - 1] += temp/10;   //向前进位
			}
			else
			{
				result[n] = temp;  
			}
			n--;
		}
		n = n + len2 - 1;   //回退 len2 - 1 位
	}

	//输出计算结果
	puts("\nThe calulation results is:");
	if(result[0] != 0)
	{
		printf("%d",result[0]);
	}
	for(i = 1; i <= len1 +len2 -1; i++)
	{
		printf("%d", result[i]);
	}
	printf("\n\n");
}

下图对程序进行简要分析：

 其实我们可以对些算法再做改进，使其效率提高约9倍。改进依据就是最开始讨论到的进制转换。我们可以把每个大数都转换成千进制数的形式，再进行手工模拟计算。例如：对于2345678 * 345678，我们可以分别把这两数从低位到高位，每三位为一组进行分组，并存放到相应数组中，从而转换成千进制数，再进行手工模拟计算。

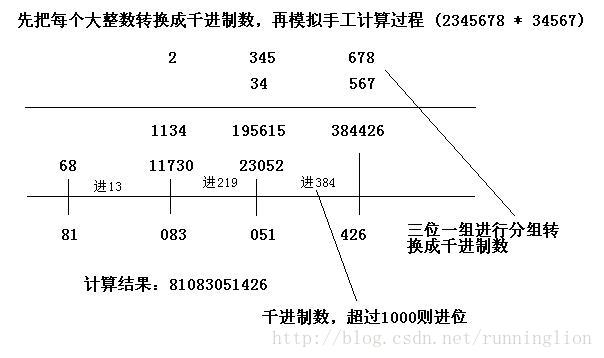
  即我们在计算时，不必一位一位地乘，而可以三位三位地乘；在累加时满1000进位。这样，我们在计算 m位整数乘以 n位整数，只需要进行 m x n / 9次乘法运算，再进行约(m + n) / 3次加法运算和(m + n) /3次取模运算。总体上，效率约是前一种算法的 9倍。那为什么不4位 4位甚至5位5位地乘呢？那不是可以提高 16 乃至 25倍效率吗？本算法在累加表中的数字时，如果用无符号长整数(范围 0至~4294967295)作为累加变量，在最不利的情况下(两个乘数的所有数字均是 9)，能够累加约4294967295/(999*999)=4300次，也就是能够准确计算任意两个均不超过 12900(每次累加的结果"值"三位，故 4300*3=12900)位的整数相乘。如果 4位 4位地乘，在最坏差条件下，能够累加约4294967295/(9999*9999)=43次，仅能够确保任意两个不超过 172位的整数相乘，所以4位或5位分组就没意义了。 

  以下程序先接收用户输入的两个数字字符串，然后调用conversion()函数把这两数分别转换成两个千进制数，并存储在相应的数组中。再利用这两个千进制数进行计算。如果两整数有负数，可先当成正数处理，最后再决定符号。这个很容易解决，但是处理起来程序代码就变得更多了，不好读懂，所以我就没处理这点，所以在输入数据时两乘数都得是正整数，程序完整源码如下：

#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#include<math.h>
#define NUM_LEN   200//数字的最大长度

/*把一个存储在scr[]数组中的数字字符串分解成整型字符串，并存放在整型数组des[]中。
分解规则：从src[]数组的高下标端，每三个元素一组，转换成相应的数字，存放到des[]
中。同样的，存放到des[]中时，也是从高下标端开始存放的。如对于src[]中的数字字符
串“12345678”，存储到des[]后，des[0]=12，des[1]=345，des[2]=678*/

void division(char src[], int des[], int len1, int len1_1)
{
	int i, flag = 0, t = len1_1 - 1, k=0;

	for(i = 0; i < len1_1; i++)   //初始化存储数字的数组
	{
		des[i] = 0;
	}

	for(i = len1 - 1; i >= 0; i--)   //以三位为一组，从src[]中分离出整数，并存放到des[]中
	{
		des[t] = des[t] + ((int)src[i] - 48) * (int)pow(10, k);
		k = (k+1)%3;
		if(++flag % 3 == 0)
		{
			t--;
			flag = 0;
		}
	}
}

void conversion(int src[], int des[], int src_len, int des_len)
{//把src[]中的每个千进制的数，转换成十进制数并存储到des[]中
	int i,k = des_len - 1,temp, flag = 0;

	for(i = src_len - 1; i >= 0; i--)
	{
		temp = src[i];

		for(flag = 0; flag < 3; flag++)
		{
			des[k--] = temp%10;
			temp = temp / 10;
		}
	}
}

void main()
{

	char num1[NUM_LEN], num2[NUM_LEN];
	puts("Please input the first number:");
	gets(num1);
	puts("\nPlease input the second number:");
	gets(num2);

	//由输入的数字串num1得到千进制整型数组arr1
	int len1 = strlen(num1);
	int len1_1 = (len1%3 == 0)?(len1/3):(len1/3 + 1);
	int *arr1 = (int *)malloc(sizeof(int) * len1_1);   //乘数1
	division(num1, arr1, len1, len1_1);

	//由输入的数字串num2得到千进制整型数组arr2
	int len2 = strlen(num2);	
	int len2_2 = (len2%3 == 0)?(len2/3):(len2/3 + 1);
	int *arr2 = (int *)malloc(sizeof(int) * len2_2);   //乘数2
	division(num2, arr2, len2, len2_2);

	int *result = (int *)malloc(sizeof(int) * (len1_1 + len2_2));   //存放结果的数组
	int *result_t = (int *)malloc(sizeof(int) * (len1 + len2));   //存放结果的数组
	int n = len1_1 + len2_2 - 1;
	for(int i = 0; i <= n; i++)
	{
		result[i] = 0;   //初始化结果数组
	}

	for(i = len1_1 - 1; i >= 0; i--)
	{
		int p = arr1[i];
		for(int k = len2_2 - 1; k >= 0; k--)
		{
			unsigned long temp = result[n] + p * arr2[k];
			if(temp >= 1000)   //如果temp>=10，则应该进位
			{
				result[n] = temp%1000;   //取个位
				result[n - 1] += temp/1000;   //向前进位
			}
			else
			{
				result[n] = temp;   //小于10，不用进位
			}
			n--;
		}
		n = n + len2_2 - 1;   //回退 len2 - 1 位
	}

	//result[]中的每个元素都是一个千进制的数，所以要转换成十进制数并存储到result_t[]中
	conversion(result, result_t, len1_1 + len2_2, len1 + len2);

	//输出计算结果
	puts("\nThe calulation results is:");

	if(result_t[0] != 0)
	{
		printf("%d",result_t[0]);
	}

	for(i = 1; i <= len1 + len2 -1; i++)
	{
		printf("%d", result_t[i]);
	}

	printf("\n\n");

}

下面再谈谈如何用分治法来解决大整数乘法问题：

  设 x 和 y 都是 n 位的二进制整数，现在要计算它们的乘积 xy ，显然我们可以用一般的方法来计算。但是这样计算步骤太多，效率低下。如果将每 2 个 1 位数的乘法或加法看作一步运算，那么这种方法要作 O(n^2) 步运算才能求出乘积 xy 。那么我们如何来设计一个更有效的方法来实现大整数乘法呢？

  我们可以把x、y分别分解为左、右两半，每一半长度为 n/2，如：x = 10110110, 则 xl = 1011，xr = 0110。由此可得

   xy= (2^n * xl * yl) + 2^(n/2)(xl * yr + xr * yl) + (xr * yl)

此表达式的复杂性在于 4 个乘法运算。然而，我们还可以继续推导，使它简化为 3 次乘法运算，化简后的式子如下：

         xy= (xl * yl)2^n +[(xl - xr)(yr - yl) + (xl * yl) + (xr * yr)]2^(n/2) + (xr * yr)   (1)

显然，在(1)式中，只有三次乘法运算 (xl * yl)、(xl - xr)(yr - yl)、(xr * yr)。从而算法复杂度就会从蛮力计算时的 n^2 降到(3/4)n^2。

  下面给出算法描述：

function MULT(X，Y，n); 
{x和y为2个小于2n的整数，返回结果为x和y的乘积xy} 
begin    
	s:=sign(x) * sign(y); {s为 x 和 y 的符号乘积}   
	x:=abs(x);    
	y:=abs(y); {x 和 y 分别取绝对值}   
	if n=1 then       
		if (x = 1) and (y = 1) then return(s)                       
				 else return(0)          
		else begin                  
			xl = x 的左边n/2位;                 
			xr = x 的右边n/2位;
			yl = y 的左边n/2位;                 
			yr = y 的右边n/2位;                 
			ml = mult(x1, yl, n/2);  //计算 (xl * yl)               
			m2 = mult(xl - xr, yr - yl, n/2);   //计算 (xl - xr)(yr - yl)                 
			m3 = mult(xr, yr, n/2);   //计算 (xr * yr)               
			s = s*(m1*2n+(m1+m2+m3)*2n/2+m3);   //计算 xy               
			return(s);               
		      end; 
end;

  上述二进制大整数乘法同样可应用于十进制大整数的乘法以提高乘法的效率减少乘法次数。下面用一个程序简单地模拟一下上面这个算法描述（注：此程序只是模拟一下上面的算法过程，由于数据类型限制，此程序并不能真正用于大整数计算，程序仅供参考）：

#include<iostream> 
#include<math.h>
using namespace std;

#define sign(num) ((num > 0) ? 1 : -1) 

int BigNumMultiply(int X, int Y, int n)  
{  
    int sign = sign(X) * sign(Y);  
    int x = abs(X);  
    int y = abs(Y);  
    if((0 == x) || (0 == y))  
        return 0;  
    if (1 == n)  
        return x*y;  
    else  
    {  
        int xl = x / (int)pow(10, (int)n/2);   
        int xr = x - xl * (int)pow(10, n/2);  
        int yl = y / (int)pow(10, (int)n/2);  
        int yr = y - yl * (int)pow(10, n/2);  
          
        int m1 = BigNumMultiply(xl, yl, n/2);  
        int m2 = BigNumMultiply(xr, yr, n/2);  
        int m3 = BigNumMultiply(xl - xr, yr - yl, n/2) + m1 + m2;  
        return sign * (m1 * (int)pow(10, n) + m3 * (int)pow(10, n/2) + m2);  
    }  
}  
int main()  
{  
    long int x = 99999;  
    long int y = 100;  
    cout<<"x * y = "<<BigNumMultiply(x, y, 4)<<endl;  
    cout<<"x * y = "<<x*y<<endl;  
    return 0;  
}